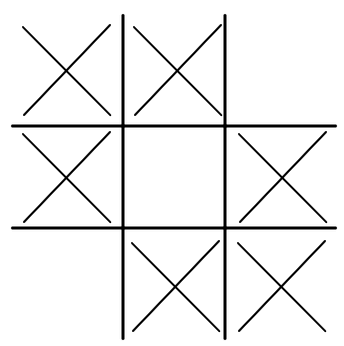
Find the max number of Xs you can fit onto a rectangular tic-tac-toe board of length l and height h without ever having 3 consecutive Xs in a row diagonally, horizontally, or vertically.
This is a fastest-codecode-golf challenge so the fastestshortest code at l = 9 and h = 9 wins.!
Input
A single line containing values l and h, representing the length and height of the tic-tac-toe board, separated by a space.
Constraints
1 ≤ l ≤ 2,147,483,647 1 ≤ h ≤ 2,147,483,647 Output
A single number representing the number of Xs that can fit on the tic-tac-toe board without three in a row
Sample Inputs and Outputs
Input -> Output 2 2 -> 4 3 3 -> 6 2 3 -> 4 4 4 -> 9 Explanation
4 Xs can fit on a 2x2 tic-tac-toe board without having 3 Xs in a row anywhere
6 Xs can fit on a 3x3 tic-tac-toe board without having 3 Xs in a row anywhere
4 Xs can fit on a 2x3 tic-tac-toe board without having 3 Xs in a row anywhere
9 Xs can fit on a 4x4 tic-tac-toe board without having 3 Xs in a row anywhere
Credits
Lukas Zenick for creating the problem
Extra Data
https://docs.google.com/spreadsheets/d/1qJvlxdGm8TocR3sh3leRIpqdzmN3bB_z8N-VrEKSCwI/edit