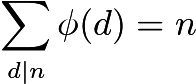##Python 2, 44 bytes
Python 2, 44 bytes
f=lambda n,d=1:d/n or-f(d)*(n%d<1)-~f(n,d+1) Less golfed:
f=lambda n:n-sum(f(d)for d in range(1,n)if n%d<1) Uses the formula that the Euler totients of the divisors of n have a sum of n:
The value of ϕ(n) can then be recursively computed as n minus the sum over nontrivial divisors. Effectively, this is doing Möbius inversion on the identity function. I used the same method in a golf to compute the Möbius function.
Thanks to Dennis for saving 1 byte with a better base case, spreading the initial value of +n into +1 for each of the n loops, done as -~.