A port of @Ajax1234's Python code in Scala.
1987 bytes, it can be golfed much more.
Golfed version. Attempt This Online!
def e(edges: List[(Int, Int)]): Set[Int] = { edges.flatMap { case (a, b) => List(a, b) }.toSet } def t[A](seq: Seq[A]): List[A] = { seq.toList } def b(edges: List[(Int, Int)]): Map[Int, Set[Int]] = { edges.foldLeft(Map[Int, Set[Int]]()) { (A, edge) => val (a, b) = edge A.updated(a, A.getOrElse(a, Set()) + b) .updated(b, A.getOrElse(b, Set()) + a) } } def f(A: Map[Int, Set[Int]]): Map[List[Int], List[List[Int]]] = { var queue = A.filter(_._2.size == 1).keys.map(node => (node, List(node), List(A(node).size))).toList var paths = Map[List[Int], List[List[Int]]]() while (queue.nonEmpty) { val (currentNode, path, degrees) = queue.head queue = queue.tail var isLeaf = true for (neighbor <- A(currentNode) -- path.toSet) { queue = queue :+ (neighbor, path :+ neighbor, degrees :+ A(neighbor).size) isLeaf = false } if (isLeaf) { val d= t(degrees) val r= t(degrees.reverse) if (paths.contains(d)) { if (!paths(d).contains(path) && !paths(d).contains(path.reverse)) { paths = paths.updated(d, paths(d) :+ path) } } else if (paths.contains(r)) { if (!paths(r).contains(path) && !paths(r).contains(path.reverse)) { paths = paths.updated(r, paths(r) :+ path) } } else { paths = paths.updated(d, List(path)) } } } paths } def c(edges: List[(Int, Int)]): Int = { val paths = f(b(edges)) var u= 0 for ((degrees, pathList) <- paths) { var subgraphs = List[List[List[Int]]]() for (path<-pathList) { val E=edges.filter { case (a, b) => !path.contains(a) && !path.contains(b) } val N= e(edges).diff(e(E)).diff(path.toSet) val newSubgraph = f(b(E ++ N.map(node => (node, node)))).keys.toList subgraphs = subgraphs :+ newSubgraph.map(_.sorted) } u+= subgraphs.distinct.size } u }
Ungolfed version. Attempt This Online!
import scala.math.Ordering.Implicits.seqOrdering object Main { def extractNodesFromEdges(edges: List[(Int, Int)]): Set[Int] = { edges.flatMap { case (a, b) => List(a, b) }.toSet } def toTuple[A](seq: Seq[A]): List[A] = { seq.toList } def buildAdjacencyList(edges: List[(Int, Int)]): Map[Int, Set[Int]] = { edges.foldLeft(Map[Int, Set[Int]]()) { (adjacencyList, edge) => val (a, b) = edge adjacencyList.updated(a, adjacencyList.getOrElse(a, Set()) + b) .updated(b, adjacencyList.getOrElse(b, Set()) + a) } } def findAllPaths(adjacencyList: Map[Int, Set[Int]]): Map[List[Int], List[List[Int]]] = { var queue = adjacencyList.filter(_._2.size == 1).keys.map(node => (node, List(node), List(adjacencyList(node).size))).toList var paths = Map[List[Int], List[List[Int]]]() while (queue.nonEmpty) { val (currentNode, path, degrees) = queue.head queue = queue.tail var isLeaf = true for (neighbor <- adjacencyList(currentNode) -- path.toSet) { queue = queue :+ (neighbor, path :+ neighbor, degrees :+ adjacencyList(neighbor).size) isLeaf = false } if (isLeaf) { val degreesTuple = toTuple(degrees) val reversedDegreesTuple = toTuple(degrees.reverse) if (paths.contains(degreesTuple)) { if (!paths(degreesTuple).contains(path) && !paths(degreesTuple).contains(path.reverse)) { paths = paths.updated(degreesTuple, paths(degreesTuple) :+ path) } } else if (paths.contains(reversedDegreesTuple)) { if (!paths(reversedDegreesTuple).contains(path) && !paths(reversedDegreesTuple).contains(path.reverse)) { paths = paths.updated(reversedDegreesTuple, paths(reversedDegreesTuple) :+ path) } } else { paths = paths.updated(degreesTuple, List(path)) } } } paths } def countUniqueSubgraphs(edges: List[(Int, Int)]): Int = { val paths = findAllPaths(buildAdjacencyList(edges)) var uniqueCount = 0 for ((degrees, pathList) <- paths) { var subgraphs = List[List[List[Int]]]() for (path <- pathList) { val remainingEdges = edges.filter { case (a, b) => !path.contains(a) && !path.contains(b) } val remainingNodes = extractNodesFromEdges(edges).diff(extractNodesFromEdges(remainingEdges)).diff(path.toSet) val newSubgraph = findAllPaths(buildAdjacencyList(remainingEdges ++ remainingNodes.map(node => (node, node)))).keys.toList subgraphs = subgraphs :+ newSubgraph.map(_.sorted) } uniqueCount += subgraphs.distinct.size } uniqueCount } def main(args: Array[String]): Unit = { println(countUniqueSubgraphs(List((1, 2), (2, 3), (3, 4), (3, 5)))) println(countUniqueSubgraphs(List((1, 2), (2, 3), (3, 4), (5, 6), (6, 7), (3, 7), (7, 8)))) println(countUniqueSubgraphs(List((1, 2), (2, 3), (3, 4), (3, 5), (3, 6), (3, 7)))) println(countUniqueSubgraphs(List((1, 2), (2, 3), (3, 4), (3, 5), (5, 6), (6, 7), (6, 8), (6, 9)))) println(countUniqueSubgraphs(List((1, 2), (2, 3), (3, 4), (4, 5), (4, 6), (7, 8), (8, 9), (6, 9), (9, 10)))) println(countUniqueSubgraphs(List((1, 2), (2, 3), (3, 4), (4, 5), (4, 6), (6, 7), (4, 8), (8, 9), (9, 10), (9, 11), (11, 12)))) println(countUniqueSubgraphs(List((1, 2), (2, 3), (2, 4), (4, 5), (4, 6), (6, 7), (7, 8), (7, 9)))) } }

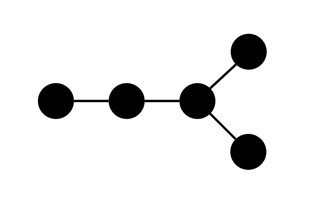
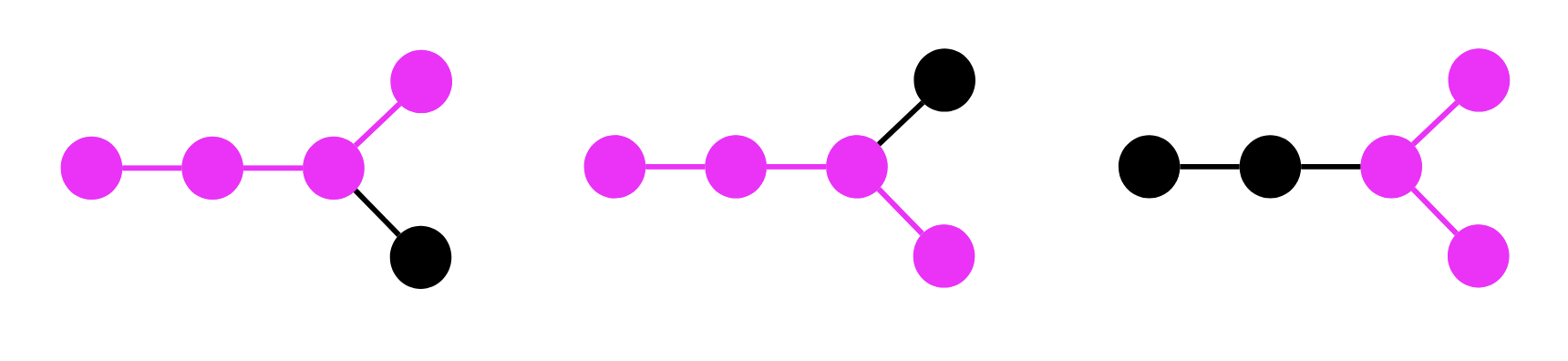
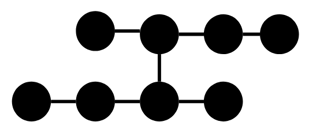
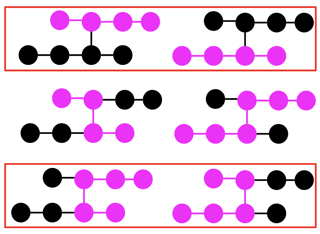
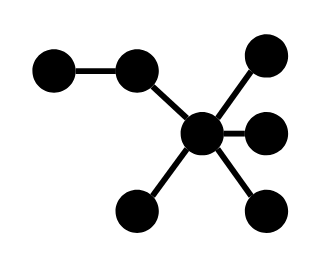
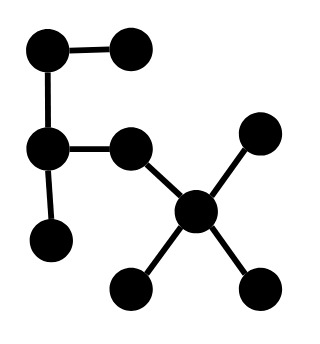
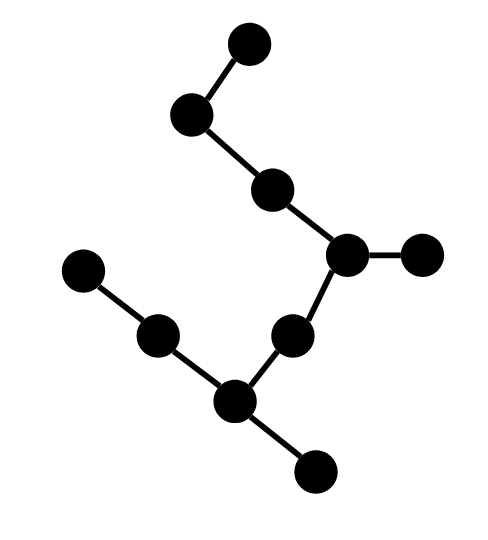
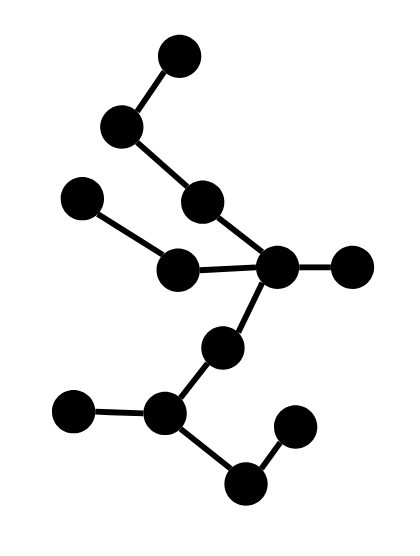
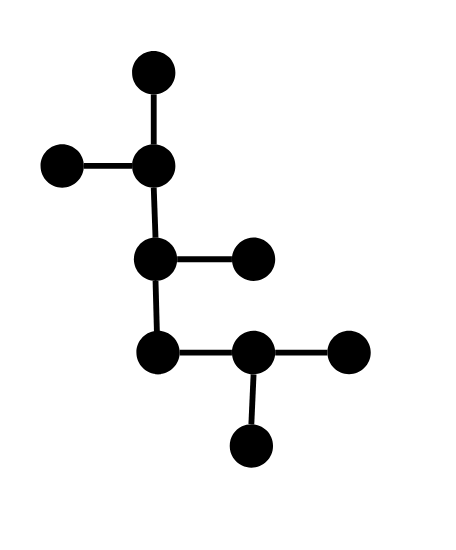
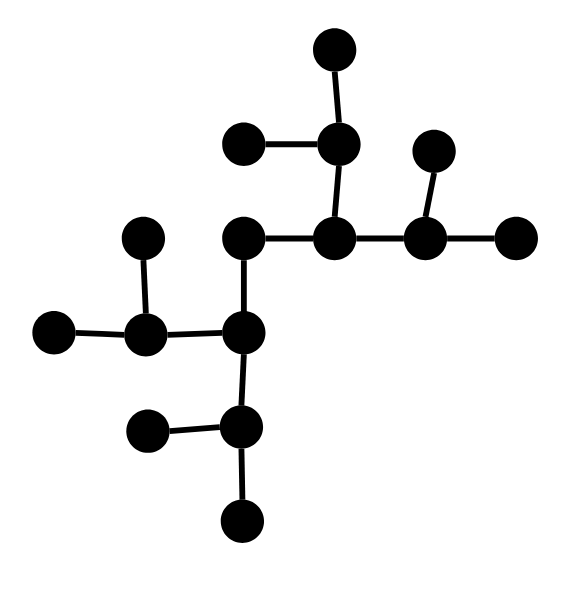
[[1, 2], [2, 3], [2, 4], [4, 5], [4, 6], [6, 7], [7, 8], [7, 9]]this has five backbones. This breaks solutions which try to check isomorphism of two paths by only comparing number of nodes connected to each node on the path. \$\endgroup\$