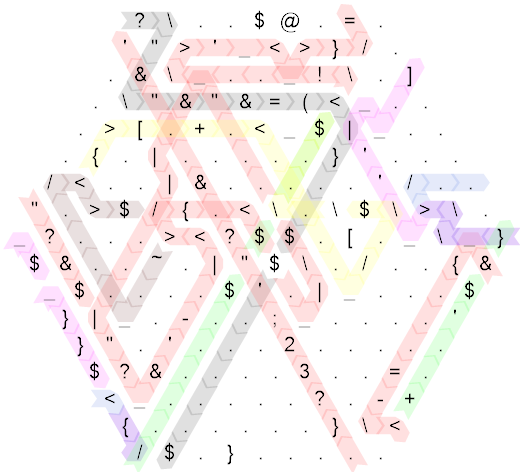
Hexagony, 212 bytes
?\..$@.=.'">'_<>}/..&\_.._!\.\].\"&"&=(<_...>\[.+.<_$|_...{.|.....}'.../<..|&.....'/..".>$/{.<\.\$\>\._?...><?$$.\[._\_}$&..~.|"$\./..{&_$....$'.|_...$}|_.-..;_....'}".'...2.....$?&....3..=.<_.....?.-+{......}\</$.}
Try it online!
Input: a single, positive integer \$n\$ on stdin.
Output: all terms of Recaman's sequence up to and including \$A(n)\$, separated by spaces (note that this means the program will print a total of \$n + 1\$ terms).
Expanded
Explanation
Apologies if this is confusing, but it's my first time with Hexagony, so rest assured that it confuses me too.
Let \$n = 6\$. The instruction pointer (IP) starts out in the NW corner, moving along the black path. ? reads \$n\$ from stdin and stores it in the current memory edge. Next, we copy \$n\$ three times while backing up the memory pointer. We also flip the memory pointer and decrement the edge it points to.
"&"&"&=(
The IP eventually wraps around to the upper left corner again, jumping over \ and looping through the rest of the black path. This loop continues until the current edge is 0, at which point the graph looks like so:
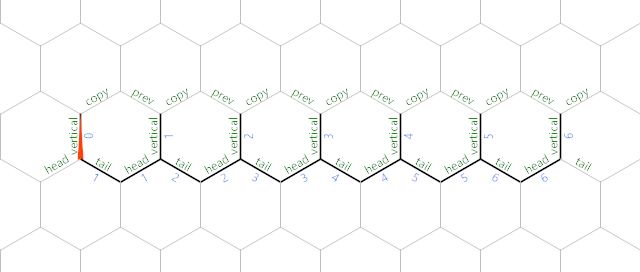
This forms the skeleton of our memory layout. Each vertical edge now stores a value \$i\$ from 0 to 6; later, these same edges will store the terms \$A(i)\$ of the sequence as they are computed. Each vertical edge also has 4 contiguous edges that are used for later computations. Let's explain them now:
head is used for several purposes, but never to store anything permanently because it is frequently overwritten by other operations.tail is generally used as a temporary variable, but it remains 0 for the last \$i\$ in the sequence, telling the program when to stop.prev stores the value of \$A(i - 1)\$copy straightforwardly stores a copy of \$i\$ or, later, \$A(i)\$
Once the program is done initializing its memory graph, it branches off the black path and onto the red path near the NE corner. First, ! prints the decimal representation of vertical to stdout. Next, we move the memory pointer to tail and test for zero:
'<
If it is zero, @ terminates the program immediately; otherwise, we move to head and set it to 32 (an ASCII space):
}=}?32
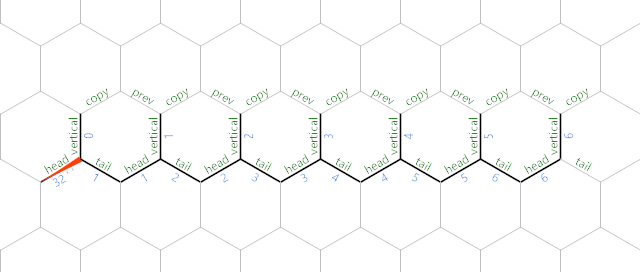
; then prints this space to stdout. Finally, we copy vertical to the next prev:
"?&"&
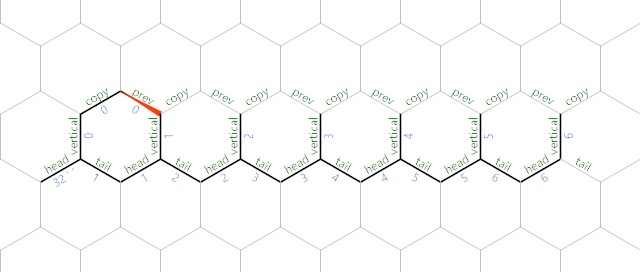
Now that the memory pointer is on the next term, we copy this term's vertical to its copy before moving to its vertical:
'&{=
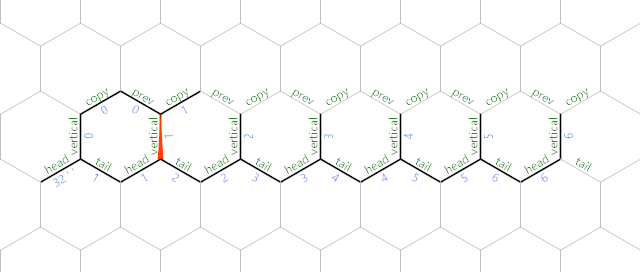
- computes prev - copy, which is really \$A(i - 1) - i\$, and stores it in vertical:
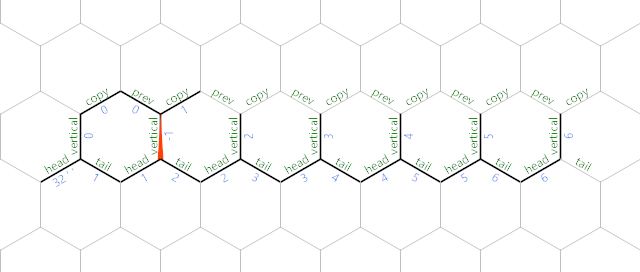
If vertical is not positive, < deflects the IP onto the green path, where + instead computes prev + copy (\$A(i - 1) + i\$) and stores it in vertical:
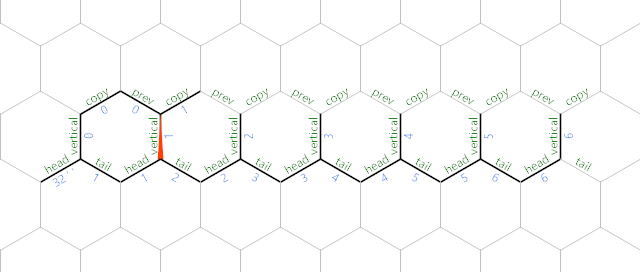
The IP then wraps around to the SW corner, eventually returning to the beginning of the red path and starting the cycle over again.
However, if vertical is positive, we have to make sure it doesn't already exist in the sequence before printing it. In this case, the < in the SE corner branches to the SE, wrapping around and staying on the red path. First, we copy vertical to head:
"?&
This puts the memory pointer in a position so that successive loops can enter at the next | mirror. Next, we copy head to the previous term's tail and move to its head.
"?&'
- computes vertical - tail (\$A(i - 1) - A(i)\$) and stores it in head. Hexagony treats zero as a negative number, so we have to do some convoluted branching to test if head is exactly zero. All that's necessary to know is that if head is zero, we've found a duplicate term, and the program will branch onto the yellow path. Otherwise, it will return to the red path at the { instruction.
If head is zero, we return to the latest term of the sequence with [, which executes the subroutine along the pink and blue paths, before + computes \$A(i - 1) + i\$) like above. We then return to the red path.
If head is not zero, we check if the current term is zero:
{<
If it is, we call the subroutine and go back to the red path through a convoluted series of mirrors. If it isn't, we move to compare the next term, returning to the aforementioned | mirror.
Images created using Timwi's Hexagony Colorer and Esoteric IDE.








