Python - 235 bytes
Requires the Python Imaging Library
from PIL import Image,ImageDraw as D x=p=141 i=Image.new('1',(x,11)) while~-p:x=p/2*x/p+2*10**19;p-=2 for c in str(x):[D.Draw(i).line((-j%3*4%7+p,j+1,-j%3*4%5+p,j+j%3),1&ord('w\22k[\36]}\23\177_'[int(c)])>>j-1)for j in range(1,8)];p+=7 i.show() The byte count assumes that the escaped characters in the string w\22k[\36]}\23\177_ are replaced with their literal equivalents (char 18, char 30, char 19, and char 127 respectively).
Output will appear as the following (it will open in your default *.bmp viewer):
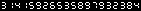
Note that this could easily be parameterized to print any number of digits you like. The following will accept an integer input from stdin, and display that many digits:
from PIL import Image,ImageDraw as D n=input() x=p=n*7|1 i=Image.new('1',(x,11)) while~-p:x=p/2*x/p+2*10**(n-1);p-=2 for c in str(x):[D.Draw(i).line((-j%3*4%7+p,j+1,-j%3*4%5+p,j+j%3),1&ord('w\22k[\36]}\23\177_'[int(c)])>>j-1)for j in range(1,8)];p+=7 i.show() Output for n=80:
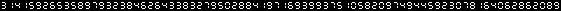
Pi Calculation
while~-p:x=p/2*x/p+2*10**19;p-=2 Yup, that's it. The formula used is the result of applying Euler's Transform to the Leibniz Series, and then factoring out each term from the remainder of the sum. The formula converges linearly; each digit requires log2(10) ≈ 3.32 iterations. For those interested in the derivation, see Appendix A.
Display
PIL is used for image generation, because it's the most convenient library that I know of. A blank 141×11 black and white bitmap is created, and then white lines are drawn on it in a seven-segment fashion. The positions required to draw each segment are stored in a bitmask string, with bits corresponding to the following positions:
000 2 1 2 1 333 5 4 5 4 666 The bit of magic (-j%3*4%7+p,j+1,-j%3*4%5+p,j+j%3) produces the x1, y1, x2, y2 tuple for each line segment. Iterated over j=1..7:
(1, 2, 3, 2) (4, 3, 4, 4) (0, 4, 0, 3) (1, 5, 3, 5) (4, 6, 4, 7) (0, 7, 0, 6) (1, 8, 3, 8) which is exactly where the lines should be.
Appendix A
Euler's Transform is a convergence acceleration technique that works for any series which displays absolute monotonic convergence. The resulting series will converge linearly, typically at the rate of one bit per term (note that if the original series was already super-linear, the resulting series will actually converge slower). The purely mathematical description is a bit hard to follow, so I'll be taking a procedural approach.
We'll start with the Leibniz Series:
Then split each term in half, combining neighboring terms:
Simplified:
Generalized:
Notice that the leading ½ didn't have a partner term, and thus was excluded from the rest of the sum. This is the first term of the transformed series. To find the next term, we repeat the process again:
http://chart.googleapis.com/chart?cht=tx&chf=bg,s,FFFFFF00&chl=%5Cfrac%7B%5Cpi%7D%7B4%7D%3D%5Cfrac%7B1%7D%7B2%7D%2B%5Cfrac%7B1%7D%7B6%7D%2B%28%5Cfrac%7B1%7D%7B6%7D-%5Cfrac%7B1%7D%7B30%7D%29-%28%5Cfrac%7B1%7D%7B30%7D-%5Cfrac%7B1%7D%7B70%7D%29%2B%28%5Cfrac%7B1%7D%7B70%7D-%5Cfrac%7B1%7D%7B126%7D%29-%28%5Cfrac%7B1%7D%7B126%7D-%5Cfrac%7B1%7D%7B198%7D%29%2B%28%5Cfrac%7B1%7D%7B198%7D-%5Cfrac%7B1%7D%7B286%7D%29-%5Cdots http://chart.googleapis.com/chart?cht=tx&chf=bg,s,FFFFFF00&chl=%5Cfrac%7B%5Cpi%7D%7B4%7D%3D%5Cfrac%7B1%7D%7B2%7D%2B%5Cfrac%7B1%7D%7B6%7D%2B%5Cfrac%7B2%7D%7B15%7D-%5Cfrac%7B2%7D%7B105%7D%2B%5Cfrac%7B2%7D%7B315%7D-%5Cfrac%7B2%7D%7B693%7D%2B%5Cfrac%7B2%7D%7B1287%7D-%5Cdots
And again:
http://chart.googleapis.com/chart?cht=tx&chf=bg,s,FFFFFF00&chl=%5Cfrac%7B%5Cpi%7D%7B4%7D%3D%5Cfrac%7B1%7D%7B2%7D%2B%5Cfrac%7B1%7D%7B6%7D%2B%5Cfrac%7B1%7D%7B15%7D%2B%28%5Cfrac%7B1%7D%7B15%7D-%5Cfrac%7B1%7D%7B105%7D%29-%28%5Cfrac%7B1%7D%7B105%7D-%5Cfrac%7B1%7D%7B315%7D%29%2B%28%5Cfrac%7B1%7D%7B315%7D-%5Cfrac%7B1%7D%7B693%7D%29-%28%5Cfrac%7B1%7D%7B693%7D-%5Cfrac%7B1%7D%7B1287%7D%29%2B%5Cdots http://chart.googleapis.com/chart?cht=tx&chf=bg,s,FFFFFF00&chl=%5Cfrac%7B%5Cpi%7D%7B4%7D%3D%5Cfrac%7B1%7D%7B2%7D%2B%5Cfrac%7B1%7D%7B6%7D%2B%5Cfrac%7B1%7D%7B15%7D%2B%5Cfrac%7B2%7D%7B35%7D-%5Cfrac%7B2%7D%7B315%7D%2B%5Cfrac%7B2%7D%7B1155%7D-%5Cfrac%7B2%7D%7B3003%7D%2B%5Cdots
And again:
http://chart.googleapis.com/chart?cht=tx&chf=bg,s,FFFFFF00&chl=%5Cfrac%7B%5Cpi%7D%7B4%7D%3D%5Cfrac%7B1%7D%7B2%7D%2B%5Cfrac%7B1%7D%7B6%7D%2B%5Cfrac%7B1%7D%7B15%7D%2B%5Cfrac%7B1%7D%7B35%7D%2B%28%5Cfrac%7B1%7D%7B35%7D-%5Cfrac%7B1%7D%7B315%7D%29-%28%5Cfrac%7B1%7D%7B315%7D-%5Cfrac%7B1%7D%7B1155%7D%29%2B%28%5Cfrac%7B1%7D%7B1155%7D-%5Cfrac%7B1%7D%7B3003%7D%29-%5Cdots http://chart.googleapis.com/chart?cht=tx&chf=bg,s,FFFFFF00&chl=%5Cfrac%7B%5Cpi%7D%7B4%7D%3D%5Cfrac%7B1%7D%7B2%7D%2B%5Cfrac%7B1%7D%7B6%7D%2B%5Cfrac%7B1%7D%7B15%7D%2B%5Cfrac%7B1%7D%7B35%7D%2B%5Cfrac%7B8%7D%7B315%7D-%5Cfrac%7B8%7D%7B3465%7D%2B%5Cfrac%7B8%7D%7B15015%7D-%5Cdots
And once more for good measure:
http://chart.googleapis.com/chart?cht=tx&chf=bg,s,FFFFFF00&chl=%5Cfrac%7B%5Cpi%7D%7B4%7D%3D%5Cfrac%7B1%7D%7B2%7D%2B%5Cfrac%7B1%7D%7B6%7D%2B%5Cfrac%7B1%7D%7B15%7D%2B%5Cfrac%7B1%7D%7B35%7D%2B%5Cfrac%7B4%7D%7B315%7D%2B%28%5Cfrac%7B4%7D%7B315%7D-%5Cfrac%7B4%7D%7B3465%7D%29-%28%5Cfrac%7B4%7D%7B3465%7D-%5Cfrac%7B4%7D%7B15015%7D%29%2B%5Cdots http://chart.googleapis.com/chart?cht=tx&chf=bg,s,FFFFFF00&chl=%5Cfrac%7B%5Cpi%7D%7B4%7D%3D%5Cfrac%7B1%7D%7B2%7D%2B%5Cfrac%7B1%7D%7B6%7D%2B%5Cfrac%7B1%7D%7B15%7D%2B%5Cfrac%7B1%7D%7B35%7D%2B%5Cfrac%7B4%7D%7B315%7D%2B%5Cfrac%7B8%7D%7B693%7D-%5Cfrac%7B8%7D%7B9009%7D%2B%5Cdots
At this point we have the first five terms, and the sixth term is evident. This should be enough to generalize, so we'll stop here. We'll start by factoring the numerators and denominators:
The denominators evidently contain a Double Factorial of 2n+1, so we'll patch that in:
Everything fits, except for the first two terms which have an unaccounted for 2 in the denominator. We can fix that by multiplying the entire expression by 2:
23 = 2·4, so:
The numerator can now be easily identified as n!.
Notice that the factor added to each successive term, n/(2n+1), approaches ½ as n becomes large, implying a linear convergence at the rate of one bit per term - this is in fact by design. A nice result, but it'd be even nicer without the factorials in there. What we can do here is to factor out each successive term from the rest of the sum, which will generate a nested expression:
http://chart.googleapis.com/chart?cht=tx&chf=bg,s,FFFFFF00&chl=%5Cfrac%7B%5Cpi%7D%7B2%7D%3D1%2B%5Cfrac%7B1%7D%7B3%7D%281%2B%5Cfrac%7B2%7D%7B5%7D%2B%5Cfrac%7B2%5Ccdot+3%7D%7B5%5Ccdot+7%7D%2B%5Cfrac%7B2%5Ccdot+3%5Ccdot+4%7D%7B5%5Ccdot+7%5Ccdot+9%7D%2B%5Cfrac%7B2%5Ccdot+3%5Ccdot+4%5Ccdot+5%7D%7B5%5Ccdot+7%5Ccdot+9%5Ccdot+11%7D%2B%5Cdots
http://chart.googleapis.com/chart?cht=tx&chf=bg,s,FFFFFF00&chl=%5Cfrac%7B%5Cpi%7D%7B2%7D%3D1%2B%5Cfrac%7B1%7D%7B3%7D%281%2B%5Cfrac%7B2%7D%7B5%7D%281%2B%5Cfrac%7B3%7D%7B7%7D%2B%5Cfrac%7B3%5Ccdot+4%7D%7B7%5Ccdot+9%7D%2B%5Cfrac%7B3%5Ccdot+4%5Ccdot+5%7D%7B7%5Ccdot+9%5Ccdot+11%7D%2B%5Cdots
http://chart.googleapis.com/chart?cht=tx&chf=bg,s,FFFFFF00&chl=%5Cfrac%7B%5Cpi%7D%7B2%7D%3D1%2B%5Cfrac%7B1%7D%7B3%7D%281%2B%5Cfrac%7B2%7D%7B5%7D%281%2B%5Cfrac%7B3%7D%7B7%7D%281%2B%5Cfrac%7B4%7D%7B9%7D%2B%5Cfrac%7B4%5Ccdot+5%7D%7B9%5Ccdot+11%7D%2B%5Cdots http://chart.googleapis.com/chart?cht=tx&chf=bg,s,FFFFFF00&chl=%5Cfrac%7B%5Cpi%7D%7B2%7D%3D1%2B%5Cfrac%7B1%7D%7B3%7D%281%2B%5Cfrac%7B2%7D%7B5%7D%281%2B%5Cfrac%7B3%7D%7B7%7D%281%2B%5Cfrac%7B4%7D%7B9%7D%281%2B%5Cfrac%7B5%7D%7B11%7D%281%2B%5Cdots%2B%5Cfrac%7Bn%7D%7B2n%2B1%7D%281%2B%5Cdots
This can be rewritten as a recurrence relation:
Where n counts backwards from ⌈log2(10)·d⌉ .. 0, where d is the number of digits required.
It might be interesting to note that the stable point of this recurrence is exactly 2 (or 4 if you've doubled it, as I have in the implmentation above), so you can save a number of iterations by initializing properly. Though, initializing to a random value you need elsewhere, and throwing a few extra iterations on the top is generally cheaper byte-wise.
