System`
The default value for the overhang parameter k (3rd argument) in ListCorrelate is None.
Internal` Predicates
Internal`LinearQ[expr, var] yields True if expr is a polynomial of exactly order one in var, and yields False otherwise.
Internal`RationalFunctionQ[expr,var] returns True if expr is a rational function of the symbol var, and returns False otherwise. Internal`RationalFunctionQ[expr,{var1, var2,...}] checks that expr is rational in each of the var_i. (ref)
Internal`RealValuedNumberQ[expr] yields True if expr is a real-valued number, and False otherwise.
Internal`RealValuedNumericQ[expr] yields True if expr is a real-valued numeric quantity, and False otherwise.
Internal`DependsOnQ[expr, form] yields True if a subexpression in expr matches form (excluding heads) and mathematically depends on form, and yields False otherwise. Takes a third argument (True/False, but behavior seems to be independent of choice) but seems to include heads also (ref)
Internal`EPolyQ[expr,var] yields True if expr is a polynomial in var and is in expanded form with respect to var. (New in 11.2)
Internal`ExceptionFreeQ[expr] yields True if expr evaluates to something that contains Infinity, DirectedInfinity, or Indeterminate, and yields False otherwise.
Internal`FundamentalDiscriminantQ[expr] yields True if expr is a fundamental discriminant Integer with the exception of 1, and False otherwise.
Internal`GregorianLeapYearQ[expr] yields True if the expr is an integer that corresponds to a leap year of the Gregorian Calendar, and False otherwise.
Internal`LiterallyOccurringQ[expr, form] yields True if a subexpression in expr explicitly matches form, ignoring any Attributes of heads that might ordinarily influence the pattern matcher, and yields False otherwise.
Internal`LiterallyAbsentQ[expr, form] yields True if no subexpression in expr matches form, and yields False otherwise.
Internal`TestIntegerQ[number, form] yields {number, True} if number is an Integer, and {number, False} otherwise.
Internal`WouldBeNumericQ[expr, {var_1, var_2, ...}] yields True if expr would become a numeric quantity if the var_i were all numeric quantities, and False otherwise.
Internal`PatternFreeQ[expr] yields True if expr does not contain any of {Alternatives, Blank, BlankNullSequence, BlankSequence, Except, Longest, Optional, OptionsPattern, OrderlessPatternSequence, PatternSequence, Repeated, RepeatedNull, Shortest}, and False otherwise.
Internal`PatternPresentQ[expr] yields True if expr contains any of {Alternatives, Blank, BlankNullSequence, BlankSequence, Except, Longest, Optional, OptionsPattern, OrderlessPatternSequence, PatternSequence, Repeated, RepeatedNull, Shortest}, and False otherwise.
Internal`PolynomialFunctionQ[expr, var] yields True if expr is a polynomial in var, and yields False otherwise. InternalPolynomialFunctionQ[expr, {var1, var2,...}] yields Trueif expr is a polynomial in all var_i, and yieldsFalse` otherwise. (more info)
Internal`RadicalMemberQ[rad, {poly1, poly2, ...}] tests whether rad belongs to the radical of the polynomial ideal generated by poly1, poly2,... (ref)
Internal`SyntacticNegativeQ[expr] gives True if expr has a minus sign vague... needs to be clarified (application)
Other Internal`'s
Internal`BinomialPrimePowerDecomposition[n,m] gives a Internal`FactoredNumber object containing the list of prime factors of the binomial coefficient (n,m) together with their exponents.
Internal`ConditionalValueBody[inputHead,{test1, test2, ...},{{msgName1,arg1A,arg1B,...},{msgName2,arg2A,arg2B,...},...},body] evaluates each of the test_i in turn and if any yields False, immediately generates the corresponding inputHead::msgName_i Message with arguments arg_iA, arg_iB,... and returns Fail; otherwise evaluates body.
Internal`CompareNumeric[prec, a, b] returns -1, 0, or 1 according to whether a is less, equal, or greater than b when compared at the precision of a or b (whichever is less) minus prec decimal digits of "tolerance". It is the fundamental operation underlying Less, Equal, Greater, LessEqual etc. for finite-precision numeric types. (ref) (more info)
Internal`DiracGammaMatrix[n, "Metric" -> {list of +/-1}, "Basis" -> ("Dirac"/"Chiral")] returns the nth Dirac Gamma matrix.
Internal`ListMin[matrix] returns matrix with rows that has all elements greater or equal to elements of another removed. (ref)
Internal`Metric is an option to Internal`DiracGammaMatrix.
Internal`JoinOrFail[list1, list2] returns the list formed by appending list2 to the end of list1.
Internal`PerfectPower[integer] gives the list of integers {n,p} such that integer is n^p.
Internal`RiccatiSolve[{a, b}, {q, r}] solves the continuous time algebraic Riccati equation. (this is a documented System function)
Internal`DiscreteRiccatiSolve[{a, b}, {q, r}] solves the discrete time algebraic Riccati equation. (this is a documented System function)
Internal`MakePolynomial[expr] returns the form of expr in terms of new variables, such that expr is polynomial in the new variables. (ref)
Internal`ToEquivalenceClass[expr, toll] replaces the floating point numbers in expr with their equivalence class representatives according to the specified tolerance toll (ref).
System`Utilities`
System`Utilities`ExprLookupAdd[expr] stores expr to memory and returns an integer (not machine sized) key for retrieval.
System`Utilities`ExprLookup[integer] returns the corresponding expr if int is a valid integer key, and returns $Failed otherwise.
System`Utilities`SymbolList[expr] returns a list of atomic Symbols (including heads) in expr.
System`Utilities`SymbolList[expr, f] applies f to each Symbol before evaluating them. System`Utilities`SymbolList[expr, f, {"Context1`", ...}] omits symbols belonging to contexts Context1` , etc.
System`Utilities`Hash* (12 functions) (more info)
Some more stuff
Reduce`FreeVariables[expr] returns a List of Symbols in expr (more info). Unclear. See this for discussion.
GroupTheory`Tools`Multisets[list, n] evaluates to a list of multisets of size n with elements drawn from list (so, repetitions are allowed, but order is irrelevant). For example, GroupTheoryToolsMultisets[{a, b, c}, 2] yields {{a,a},{a,b},{a,c},{b,b},{b,c},{c,c}} (as in this answer).
GroupTheory`Tools`MultiSubsets[list, {n, m}], if n + m = Length(list), gives the set of subsets of exactly n elements appended to the set of subsets of exactly m elements in reverse order. (equivalent to MultiSubsets[list_, {n, m}] /; Length[list] == n + m := Join @@@ Transpose[{Subsets[list, {m}, Binomial[n + m, n]], Reverse[Subsets[list, {n}, -Binomial[n + m, n]]]}] and not much faster) To figure out: What if n + m ≠ Length(list)?
GroupTheory`Tools`PartitionRagged[list, {n1, n2, ...}] seems to be equivalent to Internal`PartitionRagged[list, {n1, n2, ...}], but works even if n1 + n2 ... ≠ Length[list].
GroupTheory`Tools`IntegerPartitionCounts[n] returns a list of lists corresponding to number (counts) of integers appearing in each partition. (the correspondence with IntegerPartitions[n] appears to be reversed).
GroupTheory`Tools`ConsecutiveReplace[expr,{patt1->list1, patt2->list2,...}] replaces elements of expr (Head usually List) that match patt1, patt2, ... with elements of list1, list2 ... in the order they appear in expr. If any of the list1, list2, ... are exhausted, it wraps around.
Integrate`InverseIntegrate[expr, {x, x0, x1}] performs the definite integration by attempting various substitutions of the form u == g[x] where g[x] is an expression in the integrand. (ref) (application) (application)



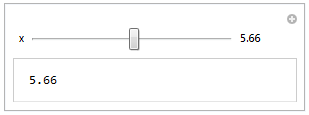
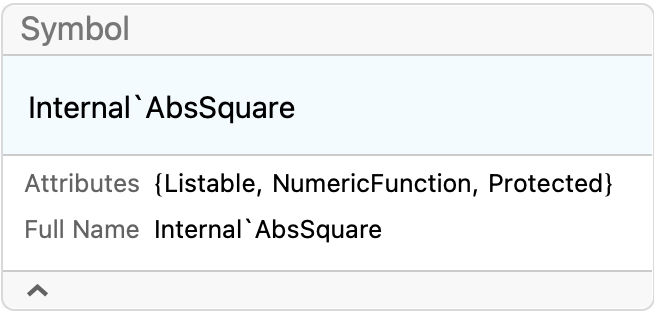
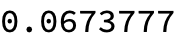
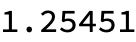

Internal`FromPiecewisein (27254) if anyone feels like writing an answer about it. $\endgroup$community wiki? $\endgroup$Internal`AbsSquare. So much time lost computing the square root inAbsorNormjust to undo it a moment later in quantum mechanical calculations. $\endgroup$