5
$\begingroup$

I am using NDSolve to solve the two equations:

func[x_, t_] := ((v[x, t] - 9/100)*(1 + u[x, t]) - 1/2*u[x, t])/u[x, t]; equ = D[u[x, t], t] - 1/20*func[x, t] + D[u[x, t]^3*(D[u[x, t], x] + D[u[x, t], {x, 3}]), x] == 0; eqv = D[v[x, t], t] + u[x, t]^2/2*(3*D[u[x, t] + D[u[x, t], {x, 2}], x])*D[v[x, t], x] - 1/10*D[v[x, t], {x, 2}] == (1 - v[x, t])*(func[x, t]^2 - (1/10*Log[(1 - v0)/(1 - v[x, t])])^2);

with the parameters and trial code (it takes about 30s on my i5 laptop):

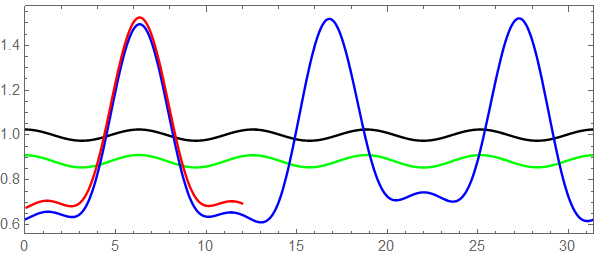
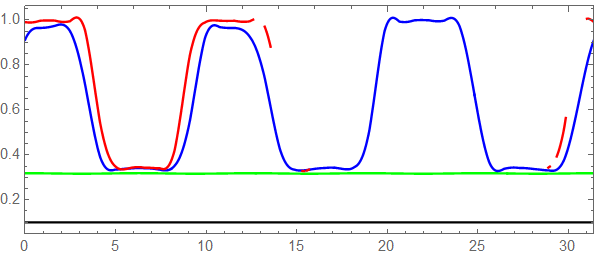
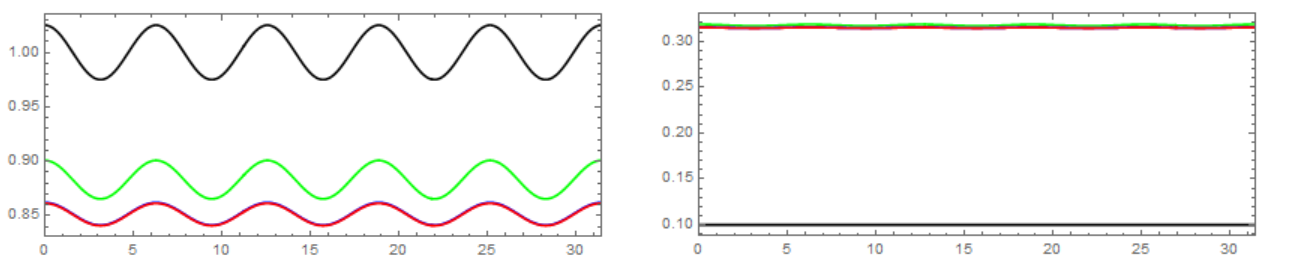
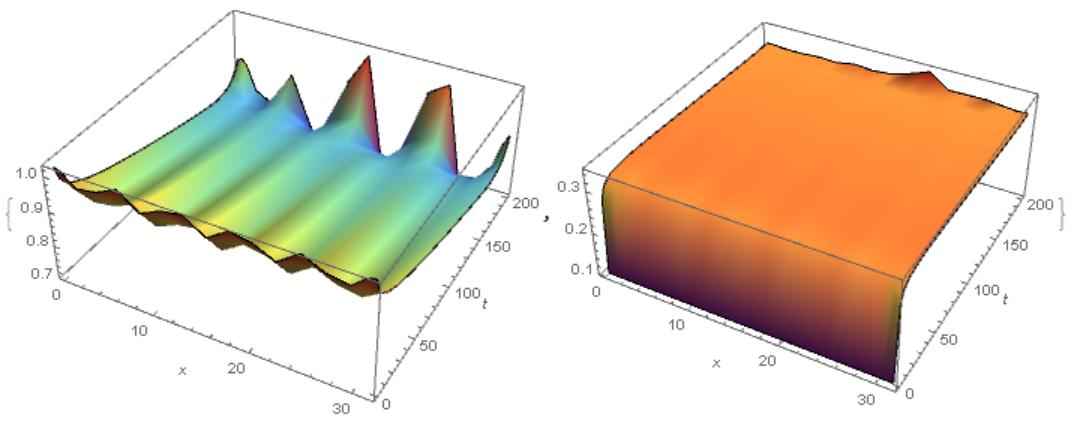
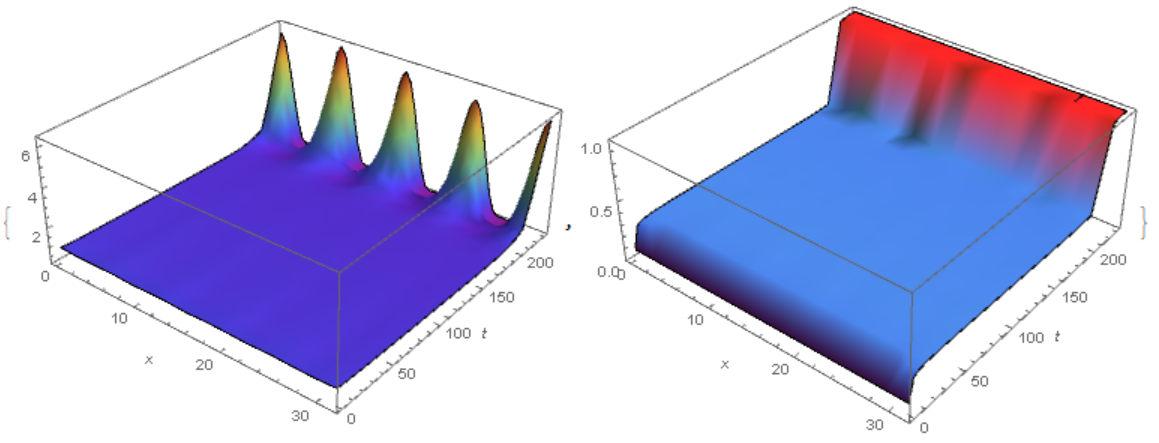
L = 10 \[Pi]; c = 1/40; v0 = 1/5; tmax = 200; eqns = {equ, eqv, u[0, t] == u[L, t], v[0, t] == v[L, t], u[x, 0] == 1 + c*Cos[x], v[x, 0] == 1/10}; {solnu, solnv} = NDSolveValue[eqns, {u, v}, {x, 0, L}, {t, 0, tmax}]

By plotting the solution, we found that after $t>100$, the solutions begin to disappear partially (see red lines for $t=101$):

Plot[{solnu[x, 0], solnu[x, 50], solnu[x, 100], solnu[x, 101]}, {x, 0, L}, PlotRange -> {{0, L}, All}, ImageSize -> 400, PlotPoints -> 80, Frame -> True, Axes -> False, AspectRatio -> 0.4, PlotStyle -> {Black, Green, Blue, Red}]

enter image description here

Plot[{solnv[x, 0], solnv[x, 50], solnv[x, 100], solnv[x, 101]}, {x, 0, L}, PlotRange -> {{0, L}, All}, ImageSize -> 400, Frame -> True, Axes -> False, AspectRatio -> 0.4, PlotStyle -> {Black, Green, Blue, Red}]

enter image description here

My thought:

By evaluating the functions at a certain position, say, $x=4$, I can understand that the disappearance of the solutions is because the solutions become complex numbers as $t$ increases.

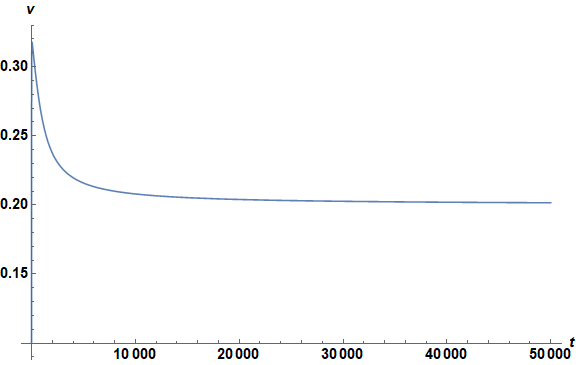
Table[solnu[4, tn], {tn, 0, tmax, 20}] (*{0.983661, 0.894927, 0.873114, 0.859587, 0.853879, 0.828441, 0.729746 - 0.0799211 I, 0.291994 + 0.0356712 I, 0.170041 - 0.089365 I, 0.166466 - 0.0930112 I, 0.166531 - 0.0929651 I}*) Table[solnv[4, tn], {tn, 0, tmax, 20}] (*{0.1, 0.313017, 0.316713, 0.316615, 0.315822, 0.432728, 0.999884 - 0.000152834 I, 0.781819 - 0.00317719 I, 0.999983 - 5.23657*10^-6 I, 1. - 1.08127*10^-7 I, 1. - 6.74084*10^-8 I}*)

In my problem, I need the solutions to be real over the entire domain. I suspected that the solutions with the imaginary parts result from the last term, Log[(1 - v0)/(1 - v[x, t])], of the 2nd equation, because the Log function itself has the domain of definition to be a real function. In addition, the function v[x, t] should not be larger than $1$, which is a physical constraint. See also the lower fig, the curves of solnv begin to vanish as the peak approaches to $1$).

My first question is:

Is it possible to add a physical constraint of 0<v[x, t]<=vlim[x,t] in the code to make the solution reasonable? Here, vlim[x, t] is determined by the solutions:

vlim[x_, t_] := Exp[4800*(1/350 - solnu[x, t]/((solnv[x, t] - 1/10)*solnu[x, t]))];

Or, is it acceptable if I only take the solutions before they vanish (i.e. $t\le 100$). In other words, is it equivalent to the constraint if one only takes the solutions from the current code, which still satisfy the constraint (e.g. by checking v[x, t])?

If you think there is something wrong with my idea, please also leave your comments and suggestion.

My second problem (solved by @Alx):

By defining a function based on the solutions, I need to numerically integrate the function at a given time, say, $t=50$. But NIntegrate runs for a very long time ... (aborted by myself). Please help me with defining such a function and then NIntegrate it correctly. Thank you in advance!

funcSol[x_, t_] := ((solnv[x, t] - 1/10)*(1 + solnu[x, t]) - solnu[x, t])/solnu[x, t]; NIntegrate[funcSol[x, 50], {x, 0, L}]
Improve this question
$\endgroup$
6
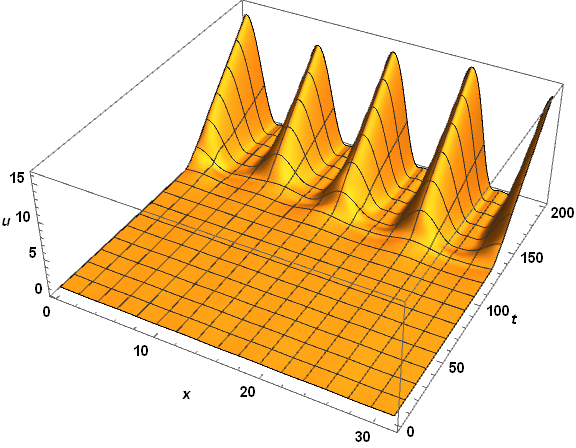
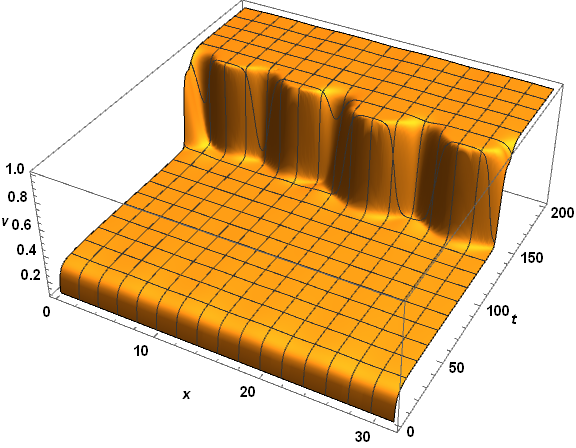
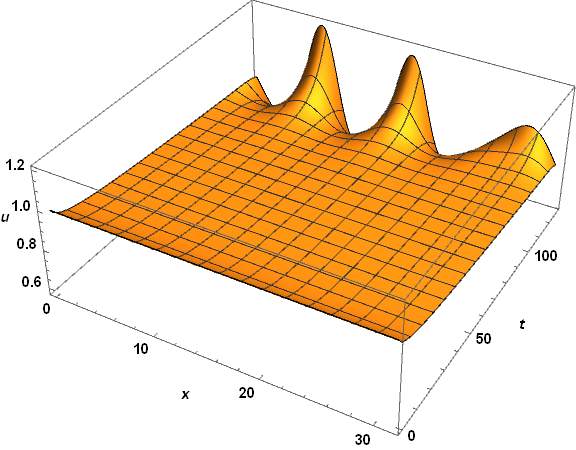
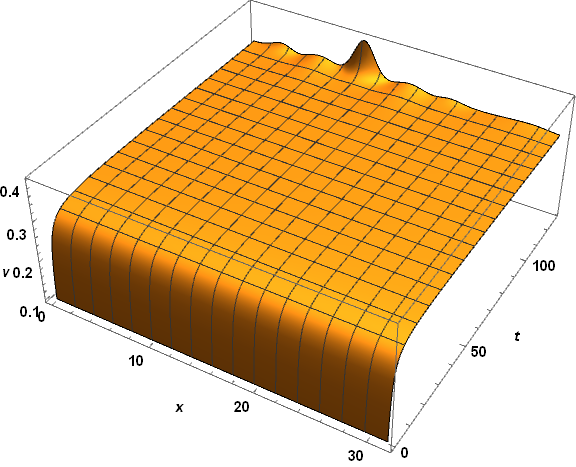
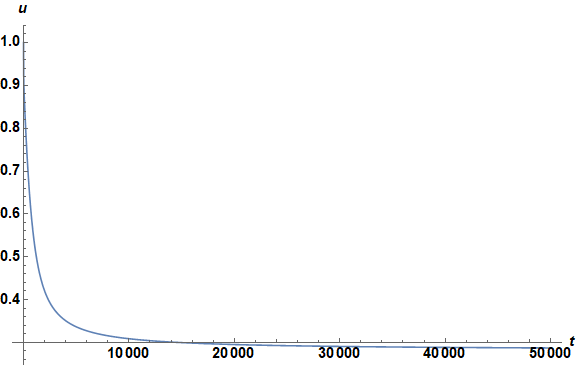
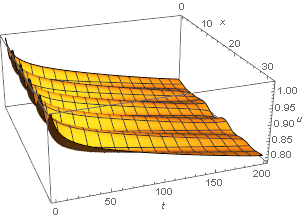
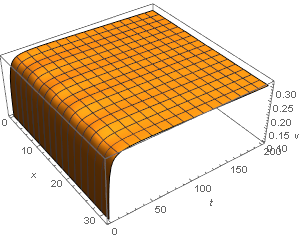
  • $\begingroup$ For the second problem use funcSol[x_?NumericQ, t_?NumericQ]:= ... so that NIntegrate will get numerical input as it expects. $\endgroup$ Commented Sep 9, 2019 at 15:24
  • $\begingroup$ Is there reason to believe that the exact solution actually is real over the entire domain? $\endgroup$ Commented Sep 10, 2019 at 2:58
  • $\begingroup$ @bbgodfrey yes, both solutions u and v should be real because they are for real physical quantities. The problem is how to add the constraint in my first question. Thank you. $\endgroup$ Commented Sep 10, 2019 at 3:01
  • $\begingroup$ Physically, how close to 1 can v become? $\endgroup$ Commented Sep 10, 2019 at 3:08
  • $\begingroup$ @user55777 From a physical point of view you should use Log[Abs[(1 - v0)/(1 - v[x, t])]] $\endgroup$ Commented Sep 10, 2019 at 4:05

3 Answers 3

Reset to default
5
$\begingroup$

As noted in the question, the computation fails when v[x, t] >= 1. This is easy to fix by replacing (1 - v[x, t]) by Max[1 - v[x, t], 10^-8] in the right side of eqv. (Results below do not change, if 10^-8 is replaced by 10^-6.) For completeness, here is a plot of the problem term. It is not large in value.

Plot[(1 - z)*(-(1/10*Log[(1 - v0)/(1 - z)])^2), {z, 0, 1}, AxesLabel -> {v, Null}, ImageSize -> Large, LabelStyle -> {Black, Bold, 15}]

enter image description here

However, the solution still behaves badly for t greater than about 100. Examining the details of these solutions suggests that the default value of MaxStepFraction is too large to resolve sharp variations in the solution. So, I steadily decreasedMaxStepFraction until the computations proceeded stably at least as far as t == tmax. This required MaxStepFraction -> 1/1000, which led to solution plots,

Plot3D[solnu[x, t], {x, 0, L}, {t, 0, tmax}, AxesLabel -> {x, t, u}, PlotRange -> All, ImageSize -> Large, LabelStyle -> {Black, Bold, 15}, PlotPoints -> 200] Plot3D[solnv[x, t], {x, 0, L}, {t, 0, tmax}, AxesLabel -> {x, t, v}, ImageSize -> Large, LabelStyle -> {Black, Bold, 15}, PlotPoints -> 200]

enter image description here

enter image description here

A phase transition appears to occur at about t == 140. A computation with MaxStepFraction -> 1/2000 produced similar plots, but with the transition at about t == 120.

Addendum: 1D solution

One might expect that setting c = 0 would yield a solution independent of x. 

L = 10 \[Pi]; c = 0; v0 = 1/5; tmax = 200; eqns = {equ, eqv, u[0, t] == u[L, t], v[0, t] == v[L, t], u[x, 0] == 1 + c*Cos[x], v[x, 0] == 1/10, WhenEvent[Max@Table[v[L (i - 1/2)/7, t], {i, 7}] > 2/5, tend = t; "StopIntegration"]}; {solnu, solnv} = NDSolveValue[eqns, {u, v}, {x, 0, L}, {t, 0, tmax}, MaxStepFraction -> 1/4000]

where WhenEvent is used to stop the integration when v[x, t] starts growing toward 1, as now requested in the question. Doing so saves a lot of run time too. The resulting plots, similar to those above but cut off at tend = 126.977, are

enter image description here

enter image description here

Evidently, these oscillations are growing from truncation errors and do not yield a 1D solution. A true 1D solution is obtained by explicitly eliminating x-dependence from the equations.

func[x_, t_] = (((v[x, t] - 9/100)*(1 + u[x, t]) - 1/2*u[x, t])/u[x, t]) /. {u[x, t] -> u[t], v[x, t] -> v[t]}; equ = Unevaluated[D[u[x, t], t] - 1/20*func[x, t] + D[u[x, t]^3*(D[u[x, t], x] + D[u[x, t], {x, 3}]), x] == 0] /. {u[x, t] -> u[t], v[x, t] -> v[t]}; eqv = Unevaluated[D[v[x, t], t] + u[x, t]^2/2*(3*D[u[x, t] + D[u[x, t], {x, 2}], x])* D[v[x, t], x] - 1/10*D[v[x, t], {x, 2}] == (1 - v[x, t])*(func[x, t]^2 - (1/10*Log[(1 - v0)/(1 - v[x, t])])^2)] /. {u[x, t] -> u[t], v[x, t] -> v[t]}; v0 = 1/5; tmax = 5 10^4; eqns = {equ, eqv, u[0] == 1, v[0] == 1/10}; {solnu, solnv} = NDSolveValue[eqns, {u, v}, {t, 0, tmax}, MaxStepSize -> 10^-2] Plot[solnu[t], {t, 0, tmax}, AxesLabel -> {t, u}, ImageSize -> Large, LabelStyle -> {Black, Bold, 15}, PlotPoints -> 200, PlotRange -> All] Plot[solnv[t], {t, 0, tmax}, AxesLabel -> {t, v}, ImageSize -> Large, LabelStyle -> {Black, Bold, 15}, PlotPoints -> 200, PlotRange -> All] {solnu[tmax], solnv[tmax]}

enter image description here

enter image description here

(* {0.287336, 0.201601} *)

which is very close to the symbolic asymptotic solution, {(9 - 100 v0)/(-59 + 100 v0), v0}. With v0 = 0.2, these are

(* {0.282051, 0.2} *)

We see from the last two plots that the asymptotic solution is not achieved for tmax less than about 10^4, much larger than tmax achievable for the 2D computations. The robustness and relatively long wavelength of the growing 2D oscillations cause me to wonder whether there is an error in the spatial derivative terms of the PDEs.

Improve this answer
$\endgroup$
19
  • $\begingroup$ Perhaps you can adjust temperal grid and spatial grid separately using e.g. MaxStepFraction -> {1/30, 1/1000}? (More discussion can be found here. ) $\endgroup$ Commented Sep 10, 2019 at 7:05
  • $\begingroup$ @xzczd I am aware of this capability, but the variation in x and in t both are extreme. $\endgroup$ Commented Sep 10, 2019 at 12:15
  • $\begingroup$ @user55777 The solution rapidly reaches a steady state but apparently becomes numerically unstable at much later time. $\endgroup$ Commented Sep 10, 2019 at 12:52
  • $\begingroup$ @bbgodfrey when observing u we can see its peaks increase in time near tmax, why did you say the solution reaches a steady state rapidly? Could you update by adding some descriptions? $\endgroup$ Commented Sep 10, 2019 at 13:18
  • $\begingroup$ @user55777 It reaches a steady state at around t == 50 but goes unstable at around t == 100. $\endgroup$ Commented Sep 10, 2019 at 13:32
1
$\begingroup$

For such a system of nonlinear equations it is necessary to use a special method of solution and a thin grid with a sufficiently large number of cells. Then the concentration function will be automatically limited and the solution will look completely different than on a coarse grid of 25 cells, which is used in the automatic solution method.

func[x_, t_] := ((v[x, t] - 9/100)*(1 + u[x, t]) - 1/2*u[x, t])/ u[x, t]; equ = D[u[x, t], t] - 1/20*func[x, t] + D[u[x, t]^3*(D[u[x, t], x] + D[u[x, t], {x, 3}]), x] == 0; eqv = D[v[x, t], t] + u[x, t]^2/2*(3*D[u[x, t] + D[u[x, t], {x, 2}], x])* D[v[x, t], x] - 1/10*D[v[x, t], {x, 2}] == (1 - v[x, t])*(func[x, t]^2 - (1/10*Log[Abs[(1 - v0)/(1 - v[x, t])]])^2); L = 10 \[Pi]; c = 1/40; v0 = 1/5; tmax = 200; eqns = {equ, eqv, u[0, t] == u[L, t], v[0, t] == v[L, t], u[x, 0] == 1 + c*Cos[x], v[x, 0] == 1/10}; {solnu, solnv} = NDSolveValue[eqns, {u, v}, {x, 0, L}, {t, 0, tmax}, Method -> {"MethodOfLines", "SpatialDiscretization" -> {"TensorProductGrid", "MinPoints" -> 137, "MaxPoints" -> 137, "DifferenceOrder" -> "Pseudospectral"}}, MaxSteps -> 10^6] Plot[{solnu[x, 0], solnu[x, 50], solnu[x, 100], solnu[x, 101]}, {x, 0, L}, PlotRange -> {{0, L}, All}, ImageSize -> 400, PlotPoints -> 80, Frame -> True, Axes -> False, AspectRatio -> 0.4, PlotStyle -> {Black, Green, Blue, Red}] Plot[{solnv[x, 0], solnv[x, 50], solnv[x, 100], solnv[x, 101]}, {x, 0, L}, PlotRange -> {{0, L}, All}, ImageSize -> 400, Frame -> True, Axes -> False, AspectRatio -> 0.4, PlotStyle -> {Black, Green, Blue, Red}]

Figure 1

{Plot3D[solnu[x, t], {x, 0, L}, {t, 0, tmax}, Mesh -> None, ColorFunction -> "Rainbow", AxesLabel -> Automatic], Plot3D[solnv[x, t], {x, 0, L}, {t, 0, tmax}, Mesh -> None, ColorFunction -> "Rainbow", AxesLabel -> Automatic, PlotRange -> All]}

Figure 2

This method can be used up to t=270 without loss of stability, but without violation of condition v<1 only up to t=230. The result is similar to what @bbgodfrey got.

Figure 3

Improve this answer
$\endgroup$
2
  • $\begingroup$ Using Pseudospectral does delay the onset of rapidly growing oscillations a bit but it does not eliminate them. In fact, to reach the steady state that the OP apparently wants would require tmax of order 10,000! The robustness and relatively long wavelength of these growing oscillations cause me to wonder whether there is an error in the spatial derivative terms of the PDEs. $\endgroup$ Commented Sep 10, 2019 at 16:51
  • $\begingroup$ I agree that in this case the instability is suppressed at t<200, but grows rapidly at t>250. Consequently we still need to limit the concentration. Obviously, the model is unsuitable for modeling real effects. $\endgroup$ Commented Sep 11, 2019 at 5:09
1
$\begingroup$

This problem seems to be 4th one I find in this site, on which the default spatial discretization of NDSolve doesn't work well even if nothing like shock wave involves in. (BTW here are 1st one, 2nd one and 3rd one. )

The following method gives stable solution up to tmax = 200. The key point is the discretization of D[u[x, t]^3 (D[u[x, t], x] + D[u[x, t], {x, 3}]), x] in equ. We need to discretize it before the automatic symbolic differentiation happens. In other words, terms like $\frac{\partial (f g)}{\partial x}$ should be discretized as

$$\frac{\partial (f g)}{\partial x}\Biggl|_{x=x_i} \approx \frac{f(x_i+h) g(x_i+h)-f(x_i-h)g(x_i-h)}{2h}$$

Notice this scheme is different from:

$$\frac{\partial (f g)}{\partial x}\Biggl|_{x=x_i}=\left(f\frac{\partial g}{\partial x}+g\frac{\partial f}{\partial x}\right)\Biggl|_{x=x_i}\approx f(x_i) \frac{g(x_i+h)-g(x_i-h)}{2h}+g(x_i)\frac{f(x_i+h)-f(x_i-h)}{2h}$$

I'll use pdetoode for discretization, notice the periodic b.c.s are set by 5th argument of pdetoode:

func[x_, t_] := ((v[x, t] - 9/100) (1 + u[x, t]) - 1/2 u[x, t])/u[x, t]; equ = D[u[x, t], t] - 1/20 func[x, t] + D[mid[x, t], x] == 0; midexpr = u[x, t]^3 (D[u[x, t], x] + D[u[x, t], {x, 3}]); eqv = D[v[x, t], t] + u[x, t]^2/2 (3 D[u[x, t] + D[u[x, t], {x, 2}], x]) D[v[x, t], x] - 1/10 D[v[x, t], {x, 2}] == (1 - v[x, t]) (func[x, t]^2 - (1/10 Log[(1 - v0)/(1 - v[x, t])])^2); L = 10 π; c = 1/40; v0 = 1/5; tmax = 200; ic = {u[x, 0] == 1 + c*Cos[x], v[x, 0] == 1/10}; points = 300; difforder = 2; domain = {0, L}; grid = Array[# &, points, domain]; (* Definition of pdetoode isn't included in this post, please find it in the link above. *) ptoofunc = pdetoode[{u, v, mid}[x, t], t, grid, difforder, True]; rule = Thread[ptoofunc@mid[x, t] -> ptoofunc@midexpr]; ode = ptoofunc@{equ, eqv} /. rule; odeic = ptoofunc@ic; sollst = NDSolveValue[{ode, odeic}, Outer[#@#2 &, {u, v}, grid], {t, 0, tmax}(*, Method->{"EquationSimplification"->"Solve"}*)]; // AbsoluteTiming (* {2.0083, Null} *) {solu, solv} = rebuild[#, grid, -1] & /@ sollst With[{solnu = solu, solnv = solv}, Plot3D[solnu[x, t], {x, 0, L}, {t, 0, tmax}, AxesLabel -> {x, t, u}, PlotRange -> All, PlotPoints -> 100]]

enter image description here

With[{solnu = solu, solnv = solv}, Plot3D[solnv[x, t], {x, 0, L}, {t, 0, tmax}, AxesLabel -> {x, t, v}, PlotPoints -> 100, PlotRange -> All]]

enter image description here

You may have noticed it's not necessary to modify the Log[…] term in eqv with this method.

Unfortunately, for larger tmax e.g. tmax = 300, the method still becomes unstable, perhaps a even better difference scheme helps, but I haven't found any so far.

Improve this answer
$\endgroup$
8
  • $\begingroup$ it seems that you never use the boundary conditions? $\endgroup$ Commented Sep 11, 2019 at 11:31
  • $\begingroup$ @user55777 Periodic b.c. is set by 5th argument of pdetoode. $\endgroup$ Commented Sep 11, 2019 at 11:32
  • $\begingroup$ thank you for the reply. I need time to understand the method. Btw, when using a spline ic: iniu[x_] = 1 + c*BSplineFunction[RandomReal[{-1, 1}, 20], SplineClosed -> True][x/L]; I got the error "Initial condition is not a number or a rectangular array of numbers", even I set its attribute with SetAttributes[iniu0, Listable]; and used iniu0[x_] = iniu[x]; in ic = {u[x, 0] == iniu0[x], v[x, 0]...};? Please give some suggestion. $\endgroup$ Commented Sep 11, 2019 at 12:10
  • $\begingroup$ @user55777 Just check what's inside your ic, and re-visit how I make use of Listable. $\endgroup$ Commented Sep 11, 2019 at 12:16
  • $\begingroup$ it is ic = {u[x, 0] == iniu[x], v[x, 0] == 1/10}, where iniu[x] is a spline function. Sorry, i cannot really understand your question. But I understood that we should add Listable to the list of attributes of the symbol iniu, as you did. $\endgroup$ Commented Sep 11, 2019 at 12:40

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.