For situations simular to those illustrated in your example, I wouldn't use Flatten. Rather, I would use Position and FlattenAt. This pair of functions will not only handle your example but also much more complicated ones. It is easy to use because Position finds the right level expresion for you.
Let's look at two examples:
example1 = {{a, {a1}}, {b, {b1}}, {c, {c1}}}; Position[example1, {_}] (* ==>{{1, 2}, {2, 2}, {3, 2}} *)
Now we know where to apply FlattenAt
FlattenAt[example1, {{1, 2}, {2, 2}, {3, 2}}] (* ==> {{a, a1}, {b, b1}, {c, c1}} *)
Of course, in everyday situations, we would compose Position and FlattenAt:
example2 = {{a, {a1, a2}}, {b, {b1, b2}}, {c, {c1, c2}}}; FlattenAt[example2, Position[example2, {_, _}]] (* ==>{a, a1, a2, b, b1, b2, c, c1, c2} *)


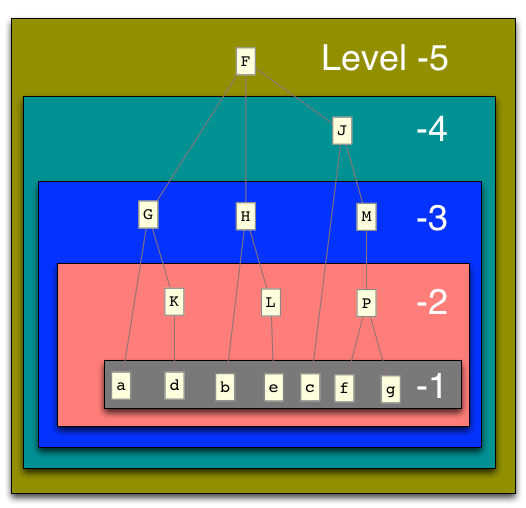

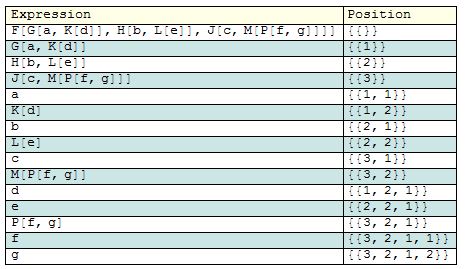
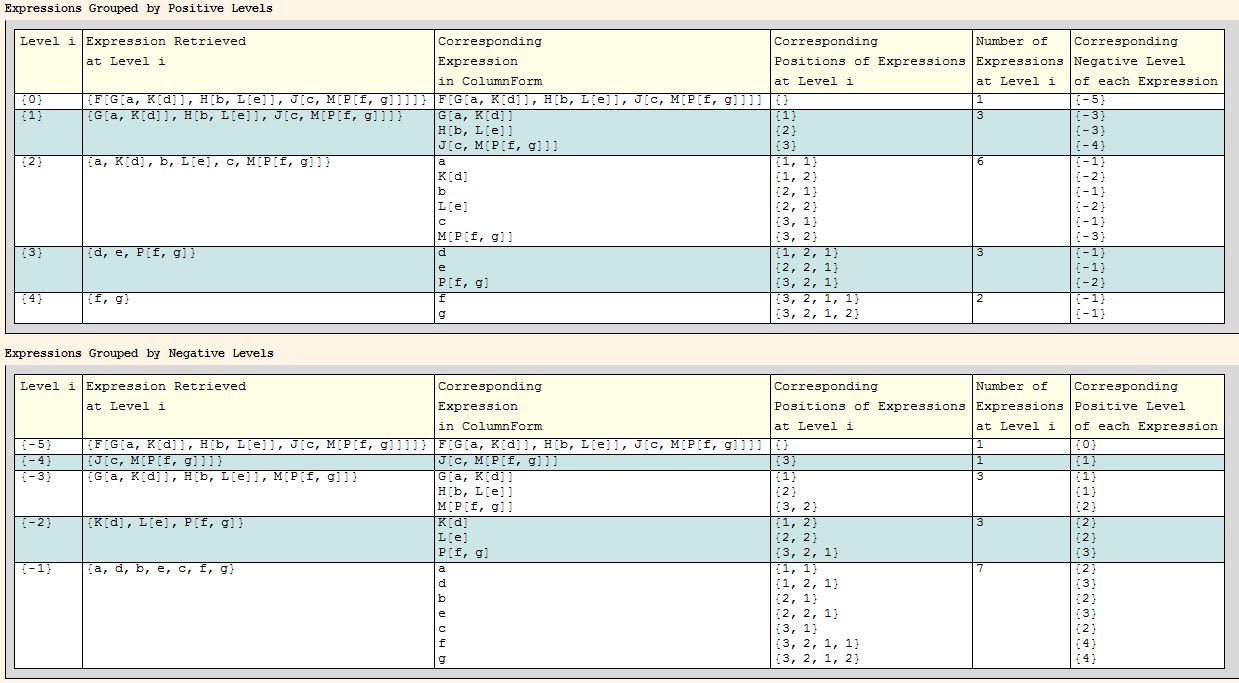
Flatten, likenor{n}$\endgroup$Map[Apply[Sequence], list, {2}]andMap[Apply[Sequence], list, {-2}]; you may useTraceto see how it works. $\endgroup$