###Math problem

vf = vi + a t /. {vi -> 0, a -> 10, t -> 60}

600

This is inconsistent with vf == 22

###Mathematica problem

Making assignments a simple variable and and an indexed variable of the same name (such as t = 60 and t[0] = 0.0) is asking for trouble. This is explained here, but may be too advanced for a beginner, so just accept that you shouldn't do it.

###Kinematics problem

For simple kinematics problems like yours, I believe it is better to express the motion as a function rather than as an expression. So

v[t_] := v0 + a t s[t_] := s0 + v0 t + a/2 t^2 

###My problem

I have no idea what you are trying to express with the reation

2 as = vf^2 + vi^2 

###Demonstrating the motion

Now let's see what I can do about making a demonstration of the kinematics. I choose to use Manipulate and Plot rather than Animate and ListPlot. Note that Manipulate supports animation. To run an animation, just click on the "+" on the right of the slider. I prefer Plot over ListPlot because motion is essentially continuous rather than discrete.

The velocity versus time plot

With[{tmax = 60}, Manipulate[ Block[{a = 10., v0 = 0.}, Plot[v[t], {t, 0, tt}, PlotRange -> {{0, tmax}, {v0, v[tmax]}}, PlotRangePadding -> Scaled[.05]]], {{tt, 1, "t"}, 1, tmax, 1, AppearanceElements -> All}]] 

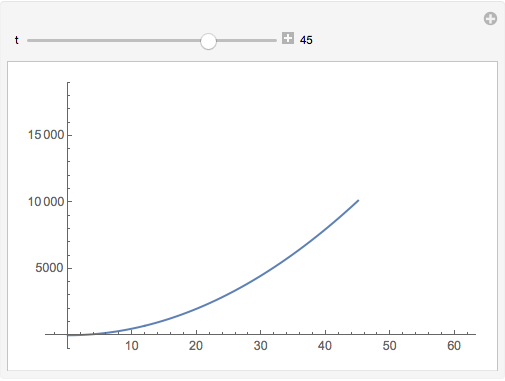
The distance versus time plot

With[{tmax = 60}, Manipulate[ Block[{a = 10., v0 = 0., s0 = 0.}, Plot[s[t], {t, 0, tt}, PlotRange -> {{0, tmax}, {s0, s[tmax]}}, PlotRangePadding -> Scaled[.05]]], {{tt, 1, "t"}, 1, tmax, 1, AppearanceElements -> All}]] 

If you insist on using Animate and ListPlot, you might do something like

With[{tmax = 20}, DynamicModule[{vData, sData}, Animate[ Block[{a = 10., v0 = 0., s0 = 0.}, vData = Table[{t, v[t]}, {t, 0, tt}]; sData = Table[{t, s[t]}, {t, 0, tt}]; ListPlot[{vData, sData}, PlotRange -> {{0, tmax}, {0., s[tmax]}}, PlotRangePadding -> Scaled[.05]]], {{tt, 0, "t"}, 0, tmax, 1}]]] 

but, in my opinion, it does not elucidate the kinematics a well as the two Manipulate expressions.