Note: this is fixed in version 10.
As I noticed in the documentation VertexConnectivity is defined as the following
The vertex connectivity of a graph $g$ is the smallest number of vertices whose deletion from $g$ disconnects $g$.
Now for a CycleGraph I expect one needs to delete at least two vertices to make the resulting graph disconnected. Please correct me if I am driven by a wrong intuition here.
opt = {VertexLabels -> "Name", ImagePadding -> 10}; graph1 = CycleGraph[8, opt]; graph2 = UndirectedGraph[Graph[{1 -> 3, 1 -> 7, 1 -> 10, 2 -> 5, 2 -> 6, 3 -> 6, 3 -> 10,4 -> 7, 4 -> 8, 4 -> 9, 5 -> 9, 6 -> 10, 7 -> 8, 8 -> 9}],opt]; Row[{graph1, graph2}] 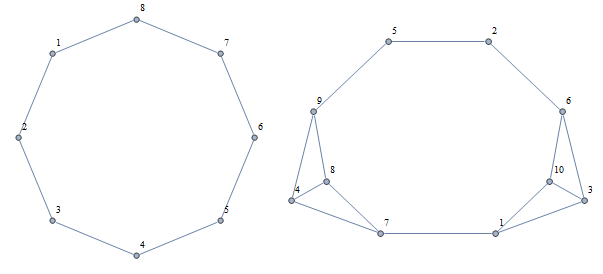
Strange!
Now Mathematica is returning this not so intuitive values for the graph1 and graph2.
VertexConnectivity /@ {graph1, graph2} {1,1}
How can one make any of these above graphs disconnected by deleting just one vertex? Can someone shade some light on this issue? EdgeConnectivity though gives understandable output for both the graphs.
