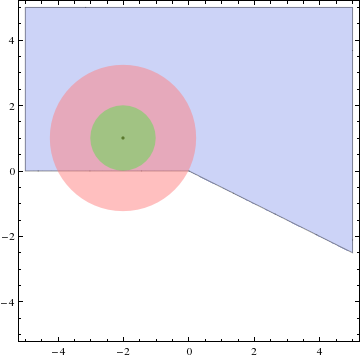
Maybe a graphical proof ?
Check your expansion by using SeriesCoefficient :
SeriesCoefficient[Log[z], {z, -2 + I, n}] // InputForm (* Piecewise[{{-((2/5 + I/5)^n/n), n >= 1}, {Log[-2 + I], n == 0}}, 0] *) Log[-2 + I] + Sum[-((2/5 + I/5)^n/n) (z - (-2 + I))^n, {n, 1, Infinity}] (* Log[-2 + I] + Log[(-(2/5) - I/5) z] *) diff = FullSimplify[ComplexExpand[f[x + I y] - Log[x + I y], TargetFunctions -> {Re, Im}], Assumptions :> {x \[Element]∈ Reals, y \[Element]∈ Reals}]; Show[RegionPlot[Abs[diff] < 10^-6, {x, -5, 5}, {y, -5, 5}], Graphics[{Black, PointSize[0.01], Point[{-2, 1}]}], Graphics[{Pink, Opacity[0.5], Disk[{-2, 1}, Sqrt[5]]}], Graphics[{Green, Opacity[0.3], Disk[{-2, 1}, 1]}]]