I try to solve this system with using NDSolve and method of iterations, and with additional bc for Cv2 consistent with initial condition. Numerical solution converges for a short time t=40. But for required T = 10000 code runs forever. It takes 5 iterations only to get solution:

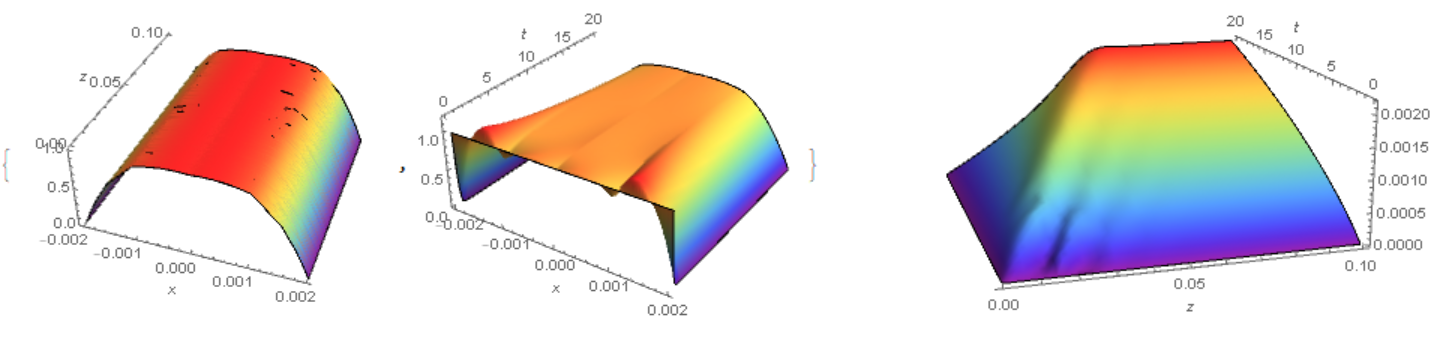
len = 0.1; l = 0.004; rad = 0.1; vz = 0.0024; kx = 8.6*10^-4; Deff = 8*10^-9; domainx = {-l/2, l/2}; domainz = {0, len}; reg = Rectangle[{-l/2, 0}, {l/2, len}]; T = 20; Cv2[0][z_, t_] := 0; a = 2*len*kx/(Pi*rad^2 - len*l); Do[C2 = NDSolveValue[{D[c[x, z, t], t] - Deff*D[c[x, z, t], {x, 2}] + Deff*D[c[x, z, t], {z, 2}] == NeumannValue[-kx*((c[x, z, t]) - Cv2[i - 1][z, t]), x == -l/2 || x == l/2], c[x, z, 0] == 1}, c, Element[{x, z}, reg], {t, 0, T}]; Cv2[i] = NDSolveValue[{ a ((C2[l/2, z, t]) - Cv[z, t]) - vz*D[Cv[z, t], {z, 1}] == D[Cv[z, t], {t, 1}], Cv[z, 0] == 0, Cv[0, t] == 0(*If[t>10^-2,C2[ l/2,0,t]-Deff/kx Derivative[1,0,0][C2][l/2,0,t],0]*)}, Cv, {z, 0, len}, {t, 0, T}];, {i, 1, 5}] 

Visualization of c and Cv

{Plot3D[C2[x, z, T], Element[{x, z}, reg], Mesh -> None, ColorFunction -> "Rainbow", PlotPoints -> 50, Boxed -> False, AxesLabel -> Automatic], Plot3D[C2[x, len/2, t], {x, -l/2, l/2}, {t, 0, T}, Mesh -> None, ColorFunction -> "Rainbow", PlotPoints -> 50, Boxed -> False, AxesLabel -> Automatic]} Plot3D[Cv2[5][z, t], {z, 0, len}, {t, 0, T}, Mesh -> None, ColorFunction -> "Rainbow", PlotPoints -> 50, Boxed -> False, AxesLabel -> Automatic]