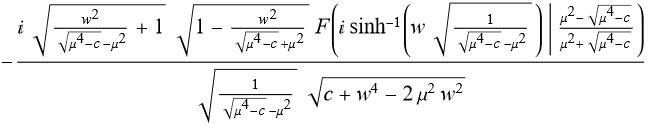In general our equation can be rewritten as a first order ODE if we multiply it by $\;\phi'(t)$ and integrate once: $$0=-\lambda \phi (t)^3 \phi'(t)+\mu ^2 \phi (t) \phi'()t+\phi ''(t) \phi'(t)$$ $$0=-\frac{c_1}{2}-\frac{\lambda}{4} \phi (t)^4 +\frac{\mu ^2}{2} \phi(t)^2 +\frac{\phi'(t)^2}{2}$$$$0=-\frac{c_1}{4}-\frac{\lambda}{4} \phi (t)^4 +\frac{\mu ^2}{2} \phi(t)^2 +\frac{\phi'(t)^2}{2}$$ This is a standard technique of recasting certain autonomusautonomous nonlinear second order ODEs to first order ones, usually used in case of elliptic functions underlying behind.
Now we can rewrite it in the following way: $$\int\frac{ dt}{\sqrt{2}}=\int \frac{d w}{\sqrt{w^4 -\mu ^2 w^2 +c}}$$$$\int\frac{ dt}{\sqrt{2}}=\int \frac{d w}{\sqrt{w^4 -2\mu ^2 w^2 +c}}$$ where $w =\sqrt{\lambda}\; \phi\;$ and $c_1 \lambda =c$. The rhs in general is an elliptic integral an cannot be calculated in terms of elementary functions (this Integrate[1/Sqrt[w^4 -2 \[Mu]^2 w^2 + c], w] // TraditionalForm yields
and an inverse function is an elliptic function expressed in terms of JacobiSN which we get when solving this ODE without initial conditions),
however for a special case when $c=\mu^4$ it reducesmight be reduced to $$\int \frac{d w}{w^2 -\mu ^2}=-\frac{arcth(\frac{w}{\mu})}{\mu}$$ and this is the case of the solution in the question.