We can generalize a solution using a function to define a square pyramidal frustum that's base-centered at the origin. The squareFrustum function computes coordinate points for Hexahedron from the prism's base and top widths, and its height. The advantage is that squareFrustum replaces the need to make manual assignments for the coordinates a, b, c, d, etc.
squareFrustum[wb_,wt_,h_] := With[{p1={-wb/2,-wb/2,0}, p5={-wt/2,-wt/2,h}}, Hexahedron[{p1, p1+{wb,0,0}, p1+{wb,wb,0}, p1+{0,wb,0}, p5, p5+{wt,0,0}, p5+{wt,wt,0}, p5+{0,wt,0}}]] We're given the slant length, but we need height so let's calculate it where b1 is the width of the base (AB=2), b2 is the width of the top (A1B1=1), and c is the slant length (AA1=$\sqrt{2}$).
height = Sqrt[c^2 - 1/2*(b1 - b2)^2] /. {b1->2, b2->1, c->Sqrt[2]}; Next, define a symbolic definition for the prism, where the base width is b1, the top width is b2, and height is h. Then, Volume gives the formula for volume, and substituting numeric values gives $\frac{7}{\sqrt{6}}$. SurfaceArea and RegionCentroid can also provide symbolic solutions.
spf = squareFrustum[b1, b2, h]; (* square pyramidal frustum *) Simplify[Volume@spf, {b1>0, b2>0, h>0}] %/.{b1->2, b2->1, h->height} ((b1^2 + b1*b2 + b2^2)*h)/3 7/Sqrt[6]
Use numeric values with squareFrustum for direct numeric solutions. First[sol] displays the coordinate points.
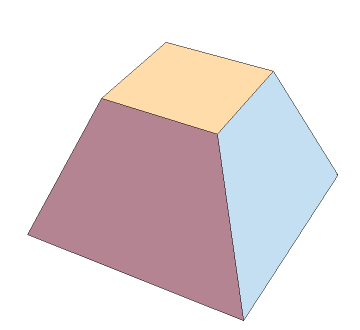
sol = squareFrustum[2, 1, height]; Volume[sol] SurfaceArea[sol] (* 7/Sqrt[6] *) (* 5 + 3*Sqrt[7] *) Graphically, we get:
Graphics3D[sol, Boxed->False]