Warning: It appears that in version 9 this tends to crash the kernel. Beware and save your work before trying!
Here's a starting point. It needs a lot more polish.
First, make a bottle:
{p1, p2, p3, p4} = Table[{i, 0.5}, {i, 4}]; if = Interpolation[{{0, 1/2}, p1, p2, p3, p4, {5, 1/2}}]; Column[{ LocatorPane[ Dynamic[{p1, p2, p3, p4}, ({p1, p2, p3, p4} = #; if = Interpolation[{{0, 1/2}, p1, p2, p3, p4, {5, 1/2}}]) &], Dynamic@Plot[if[x], {x, 0, 5}, PlotRange -> {{0, 5}, {0, 1}}]], Dynamic[ bottle = RevolutionPlot3D[{if[x], x}, {x, 0, 5}, PlotStyle -> Opacity[0.5], Mesh -> None]] }] 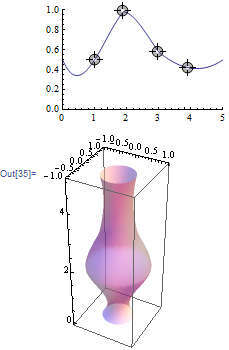
Then fill it and animate it:
volume = Derivative[-1]@FunctionInterpolation[if[x]^2, {x, 0, 5}] Table[Rasterize@ Show[bottle, RevolutionPlot3D[{0.95 if[x], x}, {x, 0, InverseFunction[volume][t]}, Mesh -> None, PlotStyle -> Blue]], {t, 0.1, volume[5], 0.1}] // ListAnimate