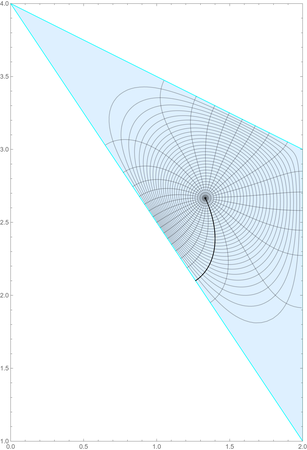
Clear["Global`*"]; a1 = 0; a2 = 1; a3 = ∞; {a, b, c} = {{2, 1}, {2, 3}, {0, 4}}; (*{a,b,c}=RandomPolygon[3][[1]];*) {w1, w2, w3} = {a, b, c} . {1, I}; center = Mean[{w1, w2, w3}]; tri = Triangle[{a, b, c}]; {α1, α2, α3} = {VectorAngle[b - a, c - a], VectorAngle[c - b, a - b], VectorAngle[a - c, b - c]}/π; f[z_] = A + B*Simplify[ Integrate[(ζ - a1)^(α1 - 1) (ζ - a2)^(α2 - 1), {ζ, 0, z}, Assumptions -> {Im[z] > 0}]]; sol = NSolve[{f[a1] == w1, f[a2] == w2}]; F[z_] = f[z] /. sol[[1]]; {F[a1], F[a2], Limit[F[t], t -> ∞]} == {w1, w2, w3}; (*True*) sol1 = z /. FindRoot[F[z] == center, {z, 1}][[1]] // ReIm; disk2upper[ w_] = (z /. Solve[(z - (u + I*v))/(z - (u - I*v)) == w, z][[1]]) /. Thread[{u, v} -> sol1]; (*ParametricPlot[ReIm[disk2upper[x+I*y]]//Evaluate,{x,y}∈\ Disk[{0,0},1 - 10^-10],Mesh->30]*) disk2triangle[x_, y_] = ReIm[F@disk2upper[x + I*y]]; g1 = {ParametricPlot[ disk2triangle[x, y], {x, y} ∈ BoundaryDiscretizeRegion@Disk[{0, 0}, 1 - 10^-10], PlotStyle -> None, BoundaryStyle -> None, MeshFunctions -> {Norm@{#3, #4} &, ArcTan @@ {#3, #4} &}, Mesh -> 30, PrologMeshShading -> {FaceForm[LightBlue]{White, EdgeForm[Cyan]Black}, tri{Black, White}}, PlotRange -> RegionBounds[tri], PlotPoints -> 60, MaxRecursion -> 2] 2, BoundaryStyle -> Black, (* the polar coordinate ofPlotRange triangle-> toAll, diskFrame *)-> False, Axes -> False], (* Graphics[{FaceForm[], EdgeForm[Black], tri}]} // Show g2 = {ParametricPlot[{x, y}, {x, y} ∈ Disk[ BoundaryDiscretizeRegion@Disk[{0, 0}, 1 - 10^-10], MeshFunctions PlotStyle -> {Function[{xNone, y}BoundaryStyle -> None, MeshFunctions -> {Norm@{Indexed[disk2triangle[x#3, y]#4} &, 1]ArcTan @@ {#3, #4} &}, Mesh Indexed[disk2triangle[x,-> y]30, 2]}],MeshShading -> {{White, Black}, Function[{xBlack, yWhite}}, ArcTan @@PlotPoints {Indexed[disk2triangle[x-> 60, y]MaxRecursion -> 2, 1]BoundaryStyle -> Black, Indexed[disk2triangle[x,PlotRange y],-> 2]}]}All, Frame -> False, Axes -> FalseFalse], Mesh -> Graphics[{30FaceForm[], 30EdgeForm[Black], Circle[]}]} // Show; *)GraphicsRow[{g1, g2}]