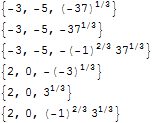It would be better to use the following :
{#[[1, 2]], #[[2, 2]]} & /@ Solve[x^2 + y == 4 && x - y == 2, {x, y}] {{-3, -5}, {2, 0}}
Since in general given a system of equations may have more than only one solution.
Another more general approach is to use Table, because of different number of variables. For example when we have 3 variables in a system :
x^2 + y == 4 && x - y == 2 && x^3 + y - z^3 == 5 We could write :
Table[ #[[a, 2]], {a, 3}] & /@ Solve[ x^2 + y == 4 && x - y == 2 && x^3 + y - z^3 == 5, {x, y, z}] Edit
Instead of specifying how many variables there are we can just use this :
Column@Apply[List, #, {2}] & @ Solve[ x^2 + y == 4 && x - y == 2 && x^3 + y - z^3 == 5, {x, y, z}] 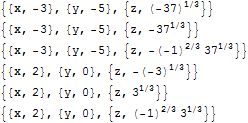
or
Column@ Apply[Composition[Part[#, 2] &, List], Solve[x^2 + y == 4 && x - y == 2 && x^3 + y - z^3 == 5, {x, y, z}], {2}]