ExpressionTreePlot (update, thanks to @Belisarius)
The GraphUtilities` package contains a function that will do the trick:
Needs["GraphUtilities`"] ExpressionTreePlot[1+Sin[x^2], Left] 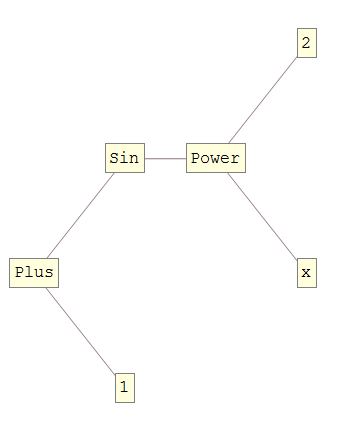
ExprTreePlot (my original response)
If you do not mind using an undocumented function, then Network`GraphPlot`ExprTreePlot can do the job:
Network`GraphPlot`ExprTreePlot[1+Sin[x^2], Left] 
The arguments to this function are:
ExprTreePlot[expr_, orientation_:Top, maxlevel_:Infinity, format_:StandardForm, options___] Of course, all the usual caveats apply: there is no official support, the feature may be removed from future versions, etc. But it gives us convenient access to all the usual choices for root node placement:
Table[ Network`GraphPlot`ExprTreePlot[1+Sin[x^2], orientation] , {orientation , {Left, Right, Top, Bottom, Center}} ] // GraphicsColumn[#, ImageSize -> {200, Automatic}, Frame -> All]& 
Recovering the TreePlot
As an alternative, we could extract the TreePlot generated by TreeForm. The complication is that TreeForm is an inert wrapper. The generation of the TreePlot happens when the front-end creates the box form. The good news is that we can use MakeBoxes to extract the TreePlot in held form:
Block[{TreePlot} , t_TreePlot := Throw @ Hold @ t ; Catch @ MakeBoxes @ TreeForm[1+Sin[x^2]] ] (* Hold[TreePlot[ {{"Plus","0"," 2\n1 + Sin[x ]"}->{"1","1","1"},...}, Top, {"Plus","0"," 2\n1 + Sin[x ]"}, AlignmentPoint->Center, AspectRatio->Automatic, ...]] *) Beware that the recovered TreePlot expression may use undocumented constructs that generate (harmless) warnings. Such warnings are normally muffled by the front-end's box generation process.
