This problem can be solved by disretizing the PDE to a set of ODEs. This approach was too cumbersome for me in 2015, but much easier nowadays because I've created pdetoode.
vdh = {x, t} \[Function] 1/(1 + h[x, t]) - h[x, t] + Log[h[x, t]/(1 + h[x, t])]; λ = t \[Function] -(1/L) int@t; eqn = D[h[x, t], t] == D[h[x, t], {x, 2}] - vdh[x, t] - λ[t]; ic = h[x, 0] == 1 + 1/Sqrt[2*π]*Exp[-((x - 10)^2/2)]; amp = 5787/1000; tmax = 1000; L = 20; points = 25; difforder = 4; domain = {0, L}; {nodes, weights} = Most[NIntegrate`GaussRuleData[points, MachinePrecision]]; midgrid = Rescale[nodes, {0, 1}, domain]; intrule = int@t -> -Subtract @@ domain weights.Map[Function[x, vdh[x, t]], midgrid] /. h[x_, t] :> h[x][t]; grid = Flatten[{0, midgrid, L}]; (*Definition of pdetoode isn't included in this post,please find it in the link above.*) ptoofunc = pdetoode[h[x, t], t, grid, difforder, True]; ode = ptoofunc[eqn] /. intrule; odeic = ptoofunc@ic; hmid = h@grid[[Length@grid/2 // Round]]; sollst = NDSolveValue[{ode, odeic, WhenEvent[hmid[t] >= amp // Evaluate, "StopIntegration"]}, h /@ grid, {t, 0, tmax}]; {{tmin, trealmax}} = sollst[[1]]["Domain"]; sol = rebuild[sollst, grid, -1]; (* Notice time is the 1st argument of sol. *) Plot3D[sol[x, t], {x, 0, L}, {t, tmin, trealmax}, PlotRange -> All] 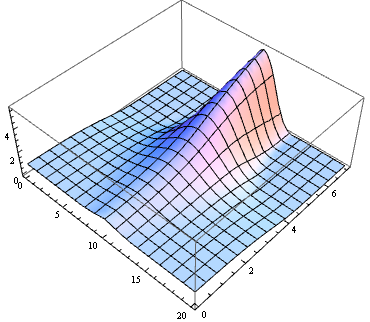
The code for numeric integration is modified from this answer.
