13
$\begingroup$

Bug introduced in 10.0 and fixed in 12.0

version 10 

$Version

"10.0 for Microsoft Windows (64-bit) (June 29, 2014)"

Consider three cases in LogLinearPlot's option Ticks:

findDivisions[{x1_, x2_}, n_] := FindDivisions[-Log[10, #] & /@ {x1, x2}, n] myTicks[x1_, x2_] := {10^-#, #} & /@ findDivisions[{x1, x2}, 10] p1 = LogLinearPlot[Log[10, x], {x, 10^-10, 10}, Ticks -> {myTicks[10^-10, 10], Automatic}]; p2 = LogLinearPlot[Log[10, x], {x, 10^-10, 10}, Ticks -> {myTicks, Automatic}]; p3 = LogLinearPlot[Log[10, x], {x, 10^-10, 10}, Ticks -> {Function[{x1, x2}, {10^-#, #} & /@ findDivisions[{x1, x2}, 10]], Automatic}]; Grid[{{"p1", "p2", "p3"}, {p1, p2, p3}}, Frame -> All]

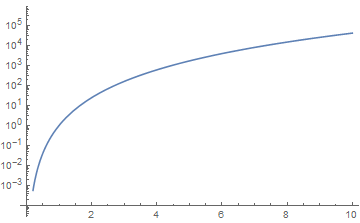
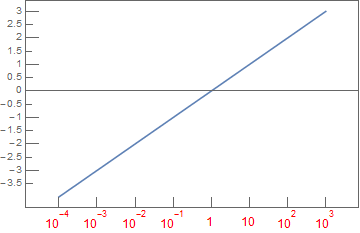
enter image description here

p1 is right.

p2 is wrong with message "Tick specification must be a list or a function".

p3 is wrong with FindDivisions's error.

this is related.

version 9

$Version

"9.0 for Microsoft Windows (32-bit) (January 24, 2013)"

All three cases well worked!

Blockquote

Improve this question
$\endgroup$
2
  • $\begingroup$ The same behavior in v.10.0.1. It is a bug: clear contradiction to the Documentation. $\endgroup$ Commented Oct 30, 2014 at 17:40
  • $\begingroup$ Somewhat related: (54578) $\endgroup$ Commented Feb 4, 2015 at 16:09

3 Answers 3

Reset to default
8
$\begingroup$

Let us see how LogPlot in Mathematica 10.0.1 handles the default and custom Ticks specifications for the log-axis:

Options[LogPlot[x^2, {x, 0, 10}], Ticks] Options[LogPlot[x^2, {x, 0, 10}, Ticks -> {Automatic, f}], Ticks] Options[LogPlot[x^2, {x, 0, 10}, Ticks -> {Automatic, f@## &}], Ticks] Options[LogPlot[x^2, {x, 0, 10}, Ticks -> {Automatic, Range[10]^2}], Ticks] 
{Ticks -> {Automatic, Charting`ScaledTicks[{Log, Exp}]}} {Ticks -> {Automatic, Visualization`Utilities`ScalingDump`scaleTicks[{Log, Exp}, f]}} {Ticks -> {Automatic, Charting`FindScaledTicks[(f[##1] &)[##1], {Log, Exp}] &}} {Ticks -> {Automatic, {{0, 1}, {Log[4], 4}, {Log[9], 9}, {Log[16], 16}, {Log[25], 25}, {Log[36], 36}, {Log[49], 49}, {Log[64], 64}, {Log[81], 81}, {Log[100], 100}}}}

According to the Documentation page for Ticks, when the functional form is used it must accept two arguments. This means that Visualization`Utilities`ScalingDump`scaleTicks must have SubValues in order to function properly:

SubValues[Visualization`Utilities`ScalingDump`scaleTicks] 
{}

There are no SubValues and the functional form returns unevaluated.

When pure function is used, we get evaluatable pure function Charting`FindScaledTicks[(f[##1] &)[##1], {Log, Exp}] &. Unfortunately, this function is implemented incorrectly - it must pass to f the plot range in the natural coordinate system (i.e. from 0.01 to 370) but instead it passes the actual plot range (i.e. from Log[0.01] to Log[370]):

Reap[Image@LogPlot[x^2, {x, 0, 10}, Ticks -> {Automatic, Sow[{##}] &}]][[2, 1]] Exp[%] 
{{-4.55639, 5.91396}} {{0.0104999, 370.171}}

One workaround is to avoid functional Ticks inside of the *Log*Plot functions and move them in the outer Show. It requires another implementation of ticks-generating function as it is already made in the CustomTicks` package which currently continues development as a part of the SciDraw package:

<< CustomTicks` Show[LogPlot[x^2, {x, 0, 10}], Ticks -> {Automatic, LogTicks}]

plot

Improve this answer
$\endgroup$
1
  • $\begingroup$ Thank a lot for your detailed explanation. $\endgroup$ Commented Nov 2, 2014 at 13:14
3
$\begingroup$

I agree this is an unfortunate situation. I guess you can pass x value range to plot and your desired division. For illustration only:

g[xmin_, xmax_] := Table[{j, Style[Superscript[10, Log10[j]], Red, 12, ScriptSizeMultipliers -> 0.7, ScriptBaselineShifts -> 1.5], {0.03, 0}}, {j, PowerRange[xmin, xmax, 10]}] /. Style[Superscript[x_, a : (0 | 1)], b__] :> Style[Superscript[x^a, ""], b] yt = Join[{#, #, {0.04, 0}} & /@ Range[-3, 3], {#, #, {0.02, 0}} & /@ Range[-3.5, 3.5, 1]];

then

LogLinearPlot[Log10[x], {x, ##}, Frame -> True, FrameTicks -> {{yt, None}, {g[##], None}}] & @@ {1/10000, 1000}

enter image description here

but agree would be nice if functioned as it does in Plot

Improve this answer
$\endgroup$
1
  • $\begingroup$ Thank you for an fine example about the Ticks $\endgroup$ Commented Nov 2, 2014 at 13:21
-3
$\begingroup$

In:

LogLinearPlot[Log[10, x], {x, 10^-10, 10},Ticks -> {myTicks, Automatic}];

myTicks is not evaluated to a list of anything; it's just a symbol. If you evaluate:

myTicks[10^-10, 10]

you get:

{{100, -2}, {1, 0}, {1/100, 2}, {1/10000, 4}, {1/1000000, 6}, {1/ 100000000, 8}, {1/10000000000, 10}}

which is a list. Don't know about Version 9, but The error message for p2 with Version 10 means exactly what it says. It seems that the code below supports my interpretation.

myTicks[x1_, x2_] := {10^-#, #} & /@ findDivisions[{x1, x2}, 10] Head[myTicks] Symbol

But, this does work:

myTicks[min_, max_] := Table[i, {i, Ceiling[min], Floor[max], 1}] LogPlot[x^2, {x, 0, 10}, Ticks -> {myTicks, Automatic}]
Improve this answer
$\endgroup$
7
  • $\begingroup$ myTicks is a function. p2 is exactly right syntax. $\endgroup$ Commented Oct 30, 2014 at 17:32
  • $\begingroup$ I don't think it's evaluated as a function without brackets and arguments. I tested it. But perhaps I made a mistake. $\endgroup$ Commented Oct 30, 2014 at 17:33
  • $\begingroup$ myTicks is just a Symbol and it is well-documented way to specify a ticks generating function. The generation of the Ticks specification is made Dynamically by a callback from the FrontEnd to the Kernel. $\endgroup$ Commented Oct 30, 2014 at 17:43
  • $\begingroup$ So, why doesn't p2 have the proper ticks? $\endgroup$ Commented Oct 30, 2014 at 17:45
  • $\begingroup$ @GeorgeWolfe It is a bug in the log-plotting code. See here the documented and expected behavior. $\endgroup$ Commented Oct 30, 2014 at 17:51

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.