4
$\begingroup$

I would like to remove facets from an octahedron 3-compound - like in the picture below.

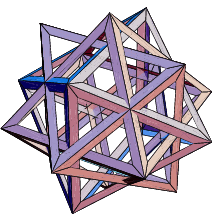
octahedron 3-compound with holes

I tried to combine these two graphics: 

PolyhedronData["OctahedronThreeCompound"]

and

Graphics3D[{Opacity[0], EdgeForm[Thickness[.03]], {PolyhedronData["OctahedronThreeCompound", "Faces"]}}]

but I failed - any tips on how to get the desired result?

Improve this question
$\endgroup$
2
  • 1
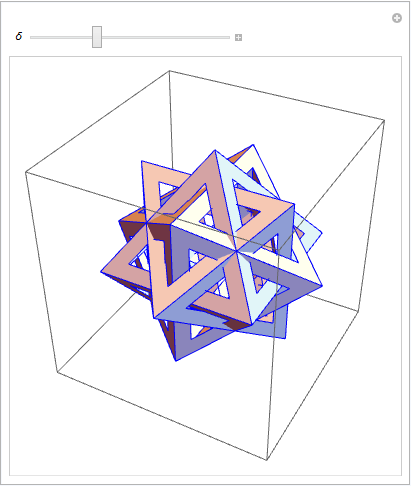
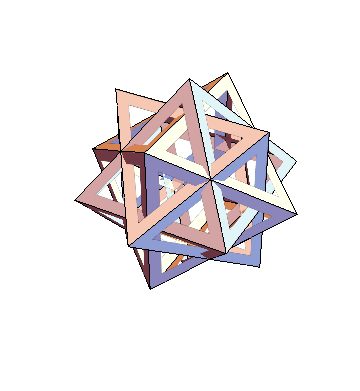
    $\begingroup$ Can you be a bit more specific? PolyhedronData gets you the image, and the documentation shows how one can extract vertices. What is it you want to do and please show what you have tried. $\endgroup$ Commented Nov 20, 2014 at 22:57
  • $\begingroup$ I was sure this was a duplicate of an older question, but it's actually not... $\endgroup$ Commented Nov 21, 2014 at 18:09

2 Answers 2

Reset to default
7
$\begingroup$

You can't get what you want with EdgeForm[Thickness[.03]], that's not what EdgeForm is meant for (that is, styles for the 1-dimensional edges).

Here is a quick solution based on post-processing:

Manipulate[ Normal[PolyhedronData["OctahedronThreeCompound", "Faces"]] /. p : Polygon[__] :> ( p /. pts : {{_?NumericQ, _, _}, __} :> Module[{cent, innervtx}, cent = Mean[pts]; innervtx = {1 - δ, δ}.{#, cent} & /@ pts; Join[pts, pts[[{1}]], innervtx, innervtx[[{1}]]] ] ) // Graphics3D[{FaceForm[White], EdgeForm[Blue], #}] &, {{δ, .1}, .01, .99}]

hollowed OctahedronThreeCompound

Improve this answer
$\endgroup$
2
  • $\begingroup$ so you are working on the next mse logo? :-) $\endgroup$ Commented Nov 22, 2014 at 8:39
  • $\begingroup$ @chris If one day we have 3D displays and 3D layout web fashion :) $\endgroup$ Commented Nov 22, 2014 at 8:43
3
$\begingroup$

Using Heike's reimplementation of the old routine PerforatePolygons[]:

PerforatePolygons[PolyhedronData["OctahedronThreeCompound"], 3/4]

octahedron 3-compound with hollowed-out faces

Now, here is a Texture[]-based dirty trick:

With[{r = 3/4 (* size of hole *)}, hole = First[ImageData[Image[Graphics[ {Polygon[CirclePoints[{1, -π/6}, 3]], {White, Polygon[CirclePoints[{r, -π/6}, 3]]}}, PlotRangePadding -> None]], Interleaving -> False]]]; tex = Transpose[ConstantArray[1 - hole, 4], {3, 1, 2}]; Graphics3D[Prepend[ Append[#, VertexTextureCoordinates -> {{0, 0}, {1, 0}, {1/2, 1}}] & /@ First[Normal[N[PolyhedronData["OctahedronThreeCompound", "Faces"]]]], Texture[tex]], Boxed -> False]

Look Ma, holes!

Improve this answer
$\endgroup$
1
  • 1
    $\begingroup$ The Texture based way is brilliant! $\endgroup$ Commented Oct 20, 2015 at 2:18

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.