7
$\begingroup$

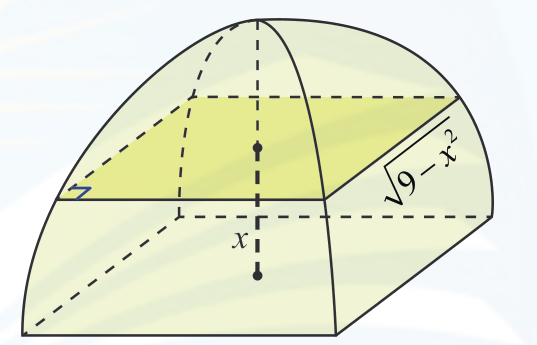
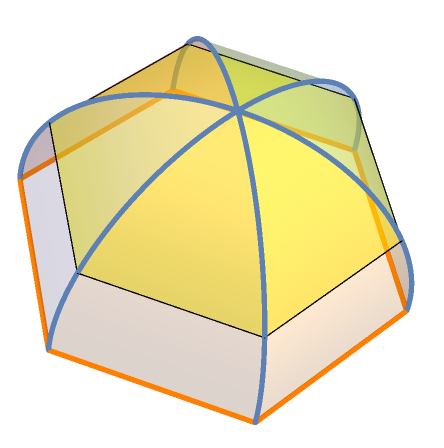
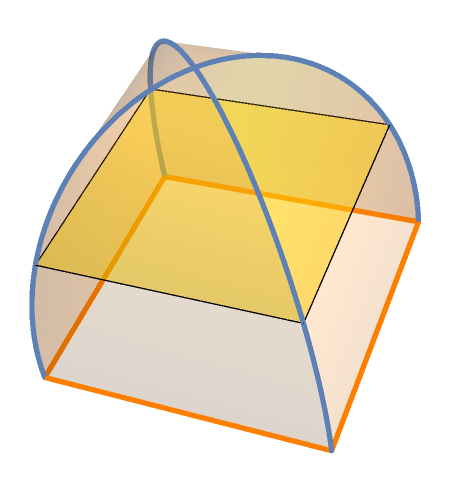
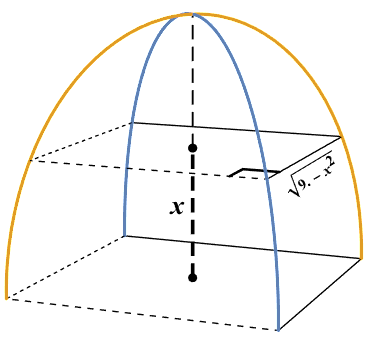
I am trying to draw this picture. I am sorry, I don't know how to start.

enter image description here

Improve this question
$\endgroup$

3 Answers 3

Reset to default
13
$\begingroup$

Edit

  • For k=6 etc.
Clear["Global`*"]; k = 6; L[θ_] := Sqrt[5^2 - θ^2]/(2 Sin[π/k]); range = FunctionDomain[L[θ], θ]; pts[θ_] := PadRight[#, 3, θ] & /@ CirclePoints[{L[θ], 0}, k]; lines = ParametricPlot3D[ pts[x], {x, Mean[{range[[1]], range[[-1]]}], range[[-1]]}, BoxRatios -> Automatic]; surface = ParametricPlot3D[{1 - s, s} . # & /@ Partition[pts[x], 2, 1, 1] // Evaluate, {x, Mean[{range[[1]], range[[-1]]}], range[[-1]]}, {s, 0, 1}, Boxed -> False, PlotStyle -> Opacity[.2], Axes -> False, PlotPoints -> 60, MaxRecursion -> 0, Mesh -> None]; Show[lines, surface, Graphics3D[{FaceForm[Directive@{Opacity[.5], Yellow}], Polygon[pts[1.5]], FaceForm[], EdgeForm[Directive@{Orange, Thick}], Polygon[pts[0]]}], Boxed -> False, Axes -> False, PlotRange -> All]

enter image description here

Edit

  • The length of the square is Sqrt[3^2 - x^2] means that it's 4 points are squares[x] as below.(the height x is the parameter).

  • For every 0<=x<=3, we join the 4 points squares[x] to build the surface.

Clear["Global`*"]; squares[x_] := {{-(Sqrt[3^2 - x^2]/2), -(Sqrt[3^2 - x^2]/2), x}, {Sqrt[3^2 - x^2]/2, -(Sqrt[3^2 - x^2]/2), x}, {(Sqrt[3^2 - x^2]/2), Sqrt[3^2 - x^2]/2, x}, {-Sqrt[3^2 - x^2]/2, Sqrt[3^2 - x^2]/2, x}}; lines = ParametricPlot3D[squares[x], {x, 0, 3}, BoxRatios -> Automatic]; surface = ParametricPlot3D[{1 - s, s} . # & /@ Partition[squares[x], 2, 1, 1], {x, 0, 3}, {s, 0, 1}, Boxed -> False, Mesh -> None, PlotStyle -> Opacity[.2], Axes -> False, PlotPoints -> 60, MaxRecursion -> 0]; Show[lines, surface, Graphics3D[{FaceForm[Directive@{Opacity[.5], Yellow}], Polygon[squares[1.5]], FaceForm[], EdgeForm[Directive@{Orange, Thick}], Polygon[squares[0]]}], Boxed -> False, Axes -> False]

enter image description here

  • To calculate the volume,one way is using Integrate to accumulate the square area which length is Sqrt[3^2 - x^2].
Integrate[(Sqrt[3^2 - x^2])^2, {x, 0, 3}]

18

or build the solid by BoundaryMeshRegion(compare with https://mathematica.stackexchange.com/a/243985/72111)

k = 4; ptss = Table[TranslationTransform[{0, 0, θ}]@* ScalingTransform[ Sqrt[3^2 - θ^2]/(2 Sin[π/k])*{1, 1, 1}]@* RotationTransform[0, {0, 0, 1}] /@ (PadRight[#, 3] & /@ CirclePoints[k]), {θ, Subdivide[3, 0, 10^3]}]; {m, n, p} = Dimensions[Rest@ptss]; bm = BoundaryMeshRegion[ Join[Flatten[Rest@ptss, 1], Union[First@ptss]], {Table[ Polygon[{{#1[[1]], #2[[1]], #2[[2]]}, {#1[[2]], #1[[1]], \ #2[[2]]}}] & @@@ Thread@{Partition[Range[1, n] + j*n, 2, 1, 1], Partition[Range[1, n] + (j + 1)*n, 2, 1, 1]}, {j, 0, m - 2}], Polygon[Range[1, n] + (m - 1)*n], Polygon /@ (Append[#, n + (m - 1)*n + 1] & /@ Partition[Range[1, n], 2, 1, 1])}] bm//Volume

18.

enter image description here

Clear["Global`*"]; k = 4; ptss = Table[ TranslationTransform[{0, 0, \[Theta]}]@* ScalingTransform[ Sqrt[3^2 - \[Theta]^2]/(2 Sin[\[Pi]/k])*{1, 1, 1}]@* RotationTransform[0, {0, 0, 1}] /@ (PadRight[#, 3] & /@ CirclePoints[k]), {\[Theta], Subdivide[3, 0, 600]}]; {m, n, p} = Dimensions[ptss]; indexes = Most@Partition[ ArrayReshape[Range[m*n], {m, n}], {2, 2}, {1, 1}, {1, 1}]; bm = BoundaryMeshRegion[ Flatten[ptss, 1], {Rest@ Map[Polygon[{#[[1, 1]], #[[1, 2]], #[[2, 2]]}] &, indexes, {2}], Map[Polygon[{#[[2, 1]], #[[2, 2]], #[[1, 1]]}] &, indexes, {2}], Polygon[Range[m*n - n + 1, m*n]]}]
Improve this answer
$\endgroup$
13
  • $\begingroup$ Your code lost at the end. How can I find volume of the solid? $\endgroup$ Commented Sep 27, 2024 at 0:14
  • $\begingroup$ @minhthien_2016 Integrate[(Sqrt[3^2 - x^2])^2, {x, 0, 3}] $\endgroup$ Commented Sep 27, 2024 at 0:49
  • $\begingroup$ Is there a picture (H) so that intersection of the plane and (H) is an quilateral triangle instead square like this question? $\endgroup$ Commented Sep 28, 2024 at 14:34
  • $\begingroup$ @minhthien_2016 set k=3. $\endgroup$ Commented Sep 28, 2024 at 23:40
  • $\begingroup$ PlotPoints -> 80, MaxRecursion -> 1, MeshFunctions -> {#5 &}, Mesh -> \ {{0, 1}}, BoundaryStyle -> None, MeshStyle -> Directive@{Thick, Blue} $\endgroup$ Commented Sep 29, 2024 at 0:08
11
$\begingroup$

A 1-1 copy:

dim = 1.5; \[Alpha] = 45 Degree; h = dim; SetOptions[Graphics3D, PlotRange -> {{-dim, dim}, {-dim, dim}, {-0.1, 2 dim}}, Boxed -> False, BoxRatios -> {1, 1, 1}, ViewPoint -> {-5, -2, 1}, ImageSize -> 220];

The graphics is a set of primitives, the data part of two ParametricPlot3D curves and a 2d-Epilog for directed Text. The elevated square is generated by a vertical lift mapped into the list of points on the floor.

Graphics3D[{ {Line[dim {{-1, -1, 0}, {1, -1, 0}, {1, 1, 0}}]}, {Dashed, Line[dim {{1, 1, 0}, {-1, 1, 0}, {-1, -1, 0}}]}, {ParametricPlot3D[{{dim Sqrt[2] Cos[\[Phi]] Cos[\[Alpha]], dim Sqrt[2] Cos[\[Phi]] Sin[\[Alpha]] , 3 Sin[\[Phi]]}, {dim Sqrt[2] Cos[\[Phi]] Cos[-\[Alpha]], dim Sqrt[2] Cos[\[Phi]] Sin[-\[Alpha]] , 3 Sin[\[Phi]]}}, {\[Phi], 0, \[Pi]}][[1]]}, {Line[(# + {0, 0, h} &) /@ (1/2 Sqrt[(2 dim)^2 - dim^2] {{-1, -1, 0}, {1, -1, 0}, {1, 1, 0}} )]}, {Dashed, Line[(# + {0, 0, h} &) /@ (1/ 2 Sqrt[(2 dim)^2 - dim^2] {{1, 1, 0}, {-1, 1, 0}, {-1, -1, 0}}) ]}, {Thickness[0.007], Line[(# + {0, 0, h} &) /@ (1/ 2 Sqrt[(2 dim)^2 - dim^2] {{-0.7, -1, 0}, {-0.7, -0.7, 0}, {-1, -0.7, 0}} )]}, {Thickness[0.01], Dashing[{0.04, 0.02}], Line[{{0, 0, 0}, {0, 0, h}}], Thickness[0.005], Dashing[{0.04, 0.02}], Line[{{0, 0, h}, {0, 0, 3}}]}, {Black, Ball[{0, 0, 0}, 0.05], Ball[{0, 0, h}, 0.05]}, {Style[{Text[x, {0.3, 0.3, 0.75}] }, Bold, 16, FontFamily -> "Times"]}}, Epilog -> {Style[ Text[Sqrt[(2 dim)^2 - x^2], Scaled[{0.85, 0.48}], Automatic, {1, 0.6}], Bold, 9, FontFamily -> "Times"]}]

Spanned Tent Skeleton

The dashing line parts could be aligned with the ViewPoint

Improve this answer
$\endgroup$
4
$\begingroup$

An approach:

f[s_, t_] := s {0, 3 Cos[t], 3 Sin[t]} + (1 - s) {3 Cos[t], 0, 3 Sin[t]} r = RotationMatrix[Pi/2, {0, 0, 1}] ParametricPlot3D[{f[0, t], f[1, t], f[s, t], r . f[s, t]}, {t, 0, Pi}, {s, 0, 1}, Mesh -> 5, MeshFunctions -> (#3 &), MeshStyle -> {Red, Thick}, PlotStyle -> {Directive[White, Thickness[0.1], Opacity[1]], Directive[White, Thickness[0.1], Opacity[1]], LightBlue, LightBlue}, Background -> Black, Boxed -> False, Axes -> False, BaseStyle -> Opacity[0.5]]

enter image description here

Improve this answer
$\endgroup$
2
  • $\begingroup$ (+1) Another good idea, but the original question is not about two half circles. I think it should be Clear[expr, r, F]; expr = Simplify[{(Sqrt[3^2 - x^2]/2), (Sqrt[3^2 - x^2]/2), x} /. x -> 3 Sin[t], Assumptions -> 0 <= t <= π/2]; r = RotationMatrix[π/2, {0, 0, 1}]; F[s_, t_] := {1 - s, s} . {expr, r . expr}; ParametricPlot3D[{F[s, t], r . F[s, t]}//Evaluate, {s, 0, 1}, {t, 0, π}] $\endgroup$ Commented Sep 27, 2024 at 12:50
  • $\begingroup$ Thanks. I should I have paid more attention $\endgroup$ Commented Sep 28, 2024 at 3:40

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.