so I wondered if there is a way to use histogram list such that it doesn't bin in quadrat mode, but given a set of 3D points, could bin over a tessellation of some regular tetrahedrons/hexagons/spheres?
3 Answers
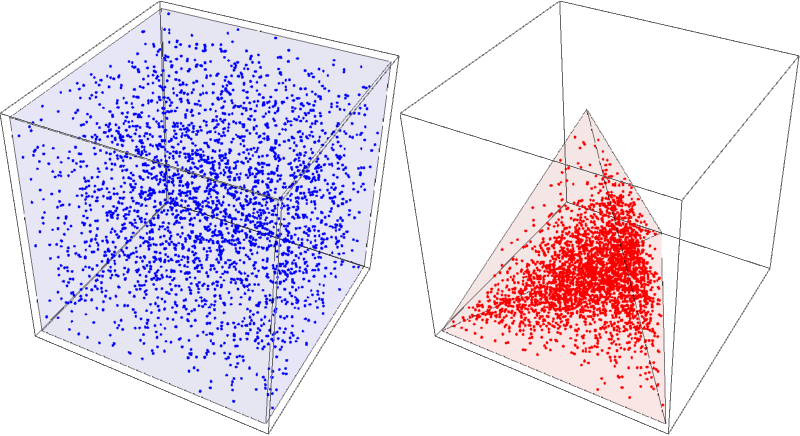
th = Tetrahedron[{{0, 0, 0}, {1, 0, 0}, {1/2, Sqrt[3]/2, 0}, {1/2, Sqrt[3]/6, Sqrt[6]/3}}]; bins = N @ NestedSymmetricSubdivision[th, 3]; centers = RegionCentroid /@ bins; nf = Nearest[centers -> "Index"]; SeedRandom[1] rp = RandomPoint[Cuboid[], 3000]; tF = FindGeometricTransform[th[[1]], Tetrahedron[][[1]]][[2]]; transformed = tF /@ (Normalize[#, Total[#]/Max[#] &] & /@ rp); Row[{Graphics3D[{Blue, Point@rp, Opacity[.05], Cuboid[]}, ImageSize -> 400], Graphics3D[{Red, Point@transformed, Opacity[.05], th}, BoxRatios -> 1, ImageSize -> 400]}] groups = GatherBy[transformed, nf[#, 1] &]; tallies = {Rescale[Length /@ groups], bins[[nf[#[[1]], 1]]] & /@ groups}; Show[Graphics3D[{FaceForm[], th, Transpose[{FaceForm[Opacity[Rescale[#, {0, 1}, {0.05, .25}], Blue]]&/@#, #2}&@@tallies]}, Boxed -> True, BoxRatios -> 1], ListPointPlot3D[groups, PlotStyle -> (ColorData[{"Rainbow", "Reversed"}]/@ tallies[[1]])], ImageSize -> Large] - $\begingroup$ Wow, your skills know no bounds, massive massive thanks for figuring these out! $\endgroup$MKF– MKF2019-03-10 13:23:32 +00:00Commented Mar 10, 2019 at 13:23
- $\begingroup$ Thank you @MKF for the kind words. $\endgroup$kglr– kglr2019-03-10 13:24:18 +00:00Commented Mar 10, 2019 at 13:24
- $\begingroup$ I feel I was little help that's all $\endgroup$MKF– MKF2019-03-10 13:24:37 +00:00Commented Mar 10, 2019 at 13:24
- 1$\begingroup$ In any case, truly amazing @kglr $\endgroup$MKF– MKF2019-03-10 13:31:11 +00:00Commented Mar 10, 2019 at 13:31
- 1$\begingroup$ @MKF, yes; thank you. Fixed now. $\endgroup$kglr– kglr2019-03-10 14:14:39 +00:00Commented Mar 10, 2019 at 14:14
This isn't an answer, just a response to the previous comment
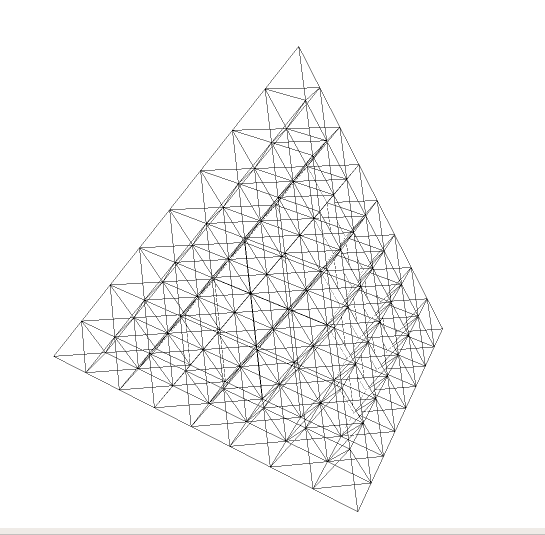
SymmetricSubdivision[Tetrahedron[pl_], k_] /; 0 <= k < 2^Length[pl] := Module[{n = Length[pl] - 1, i0, bl, pos}, i0 = DigitCount[k, 2, 1]; bl = IntegerDigits[k, 2, n]; pos = FoldList[If[#2 == 0, #1 + {0, 1}, #1 + {1, 0}] &, {0, i0}, Reverse[bl]]; Tetrahedron@Map[Mean, Extract[pl, #] & /@ Map[{#} &, pos + 1, {2}]]] NestedSymmetricSubdivision[Tetrahedron[pl_], level_Integer] /; level == 0 := Tetrahedron[pl] NestedSymmetricSubdivision[Tetrahedron[pl_], level_Integer] /; level > 0 := Flatten[NestedSymmetricSubdivision[ SymmetricSubdivision[Tetrahedron[pl], #], level - 1] & /@ Range[0, 7]] Graphics3D[ NestedSymmetricSubdivision[ Tetrahedron[{{0, 0, 0}, {1, 0, 0}, {1/2, Sqrt[3]/2, 0}, {1/2, Sqrt[ 3]/6, Sqrt[6]/3}}], 3], BaseStyle -> Opacity[0], Boxed -> False] - $\begingroup$ So the question is the following now, is there a way to convert this into a mesh, and tally all the points inside each mini tetrahedron, so that each tetrahedron has different opacity based on the number of points inside each region? $\endgroup$MKF– MKF2019-02-27 13:55:57 +00:00Commented Feb 27, 2019 at 13:55
- $\begingroup$ My guess is yes using
ListDensityPlot3D[HistogramList[pts, 10][[2]], DataRange -> the region of the tetrahedron]but with the above converted into a mesh somehow $\endgroup$MKF– MKF2019-02-27 13:56:39 +00:00Commented Feb 27, 2019 at 13:56 - 1$\begingroup$ You can easily find out if a point is in a tetrahedron using
RegionMember[Tetraherdon[{....}]][pointOfInterest]. This would be easy to repurpose for tallying the points in each tetrahedron, though it might be slow. $\endgroup$N.J.Evans– N.J.Evans2019-02-27 16:26:52 +00:00Commented Feb 27, 2019 at 16:26 - 2$\begingroup$ Taking your own code, look at
Graphics3D /@ NestedSymmetricSubdivision[ Tetrahedron[{{0, 0, 0}, {1, 0, 0}, {1/2, Sqrt[3]/2, 0}, {1/2, Sqrt[3]/6, Sqrt[6]/3}}], 1]. It's quite clear from simple visual inspection that the tetrahedra are not identical. We can verify that they have the sameVolume, but not the sameSurfaceAreaor the same shape. Of course we can still use them for binning if we want to. $\endgroup$Szabolcs– Szabolcs2019-02-28 14:49:26 +00:00Commented Feb 28, 2019 at 14:49 - 2$\begingroup$ If you can determine a center for each cell (tetrahedron or other) such that the cell would be a Voronoi cell, then you can use the same approach as in the code I linked: use Nearest to determine which cell each binned point belongs to. $\endgroup$Szabolcs– Szabolcs2019-02-28 14:50:09 +00:00Commented Feb 28, 2019 at 14:50
So I have some random points that lie in the tetrahedron, 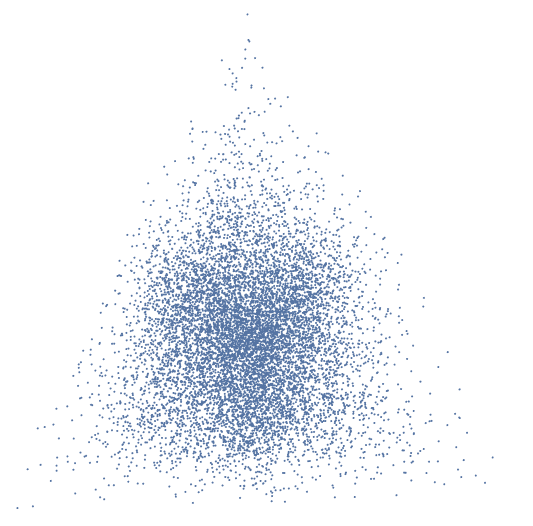 ,
,
and also calculate the centres of the tetraminos using Mean.
I apply indices = First /@ nf /@ cloud as in @Szabolcs code and now want to bin the points in each tetramino bin.
Here is histogram of the indices to check things are happening
I have tried
tally = Tally[indices]; ListDensityPlot3D[Join[cloud, List /@ Sort[tally][[All, 2]], 2], ColorFunction -> (ColorData["BeachColors"][1 - #] &)] To bin the points but to no avail.
As for @N.J.Evans response, I define RegionMemberFunctions as
Map[RegionMember, NestedSymmetricSubdivision[ Tetrahedron[{{0, 0, 0}, {1, 0, 0}, {1/2, Sqrt[3]/2, 0}, {1/2, Sqrt[ 3]/6, Sqrt[6]/3}}], 3]]; But if I try to now tally/bin the points with
Table[Map[regionmemberfunctions[[i]], cloud], {i, 1, Length[NestedSymmetricSubdivision[ Tetrahedron[{{0, 0, 0}, {1, 0, 0}, {1/2, Sqrt[3]/2, 0}, {1/2, Sqrt[ 3]/6, Sqrt[6]/3}}], 3]]}]; It takes forever... Any ideas greatly appreciated!
- $\begingroup$ I think perhaps binning over the tetraminos and using something like this is great mathematica.stackexchange.com/questions/17260/… $\endgroup$MKF– MKF2019-03-03 12:05:11 +00:00Commented Mar 3, 2019 at 12:05
- $\begingroup$ And maybe via
WhichorCountthere could be some success $\endgroup$MKF– MKF2019-03-03 13:47:09 +00:00Commented Mar 3, 2019 at 13:47

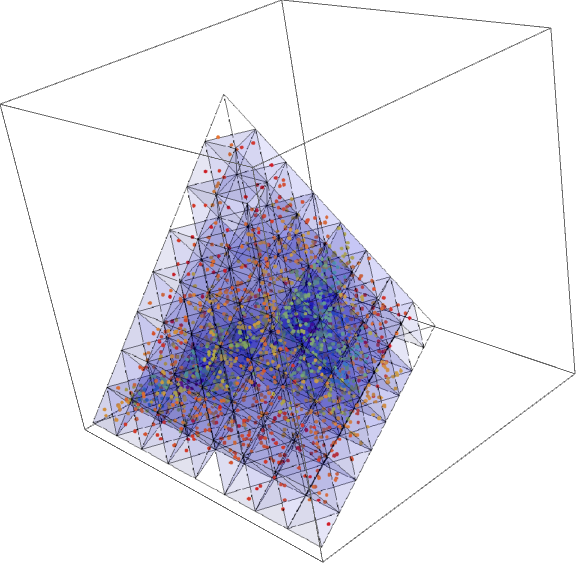
SmoothKernelDistribution. It works in all dimensions. $\endgroup$