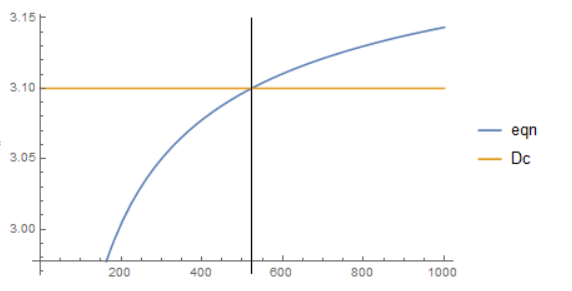
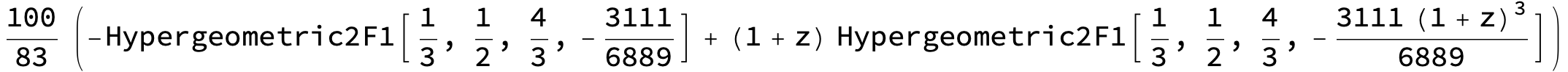We will demonstrate that the exact formula for $z$ reads: $$z=\wp\bigg(\frac{\sqrt{\Omega_M}}{2}D_c+\wp^{-1}\big(1;0,-\frac{4\Omega_\Lambda}{\Omega_M}\big);0,-\frac{4\Omega_\Lambda}{\Omega_M}\bigg)-1$$ where $\wp(x;g_2,g_3)$ is the Weierstrass elliptic function, which yields a value $w$ in the elliptic integral $$x=\int^{w}_{\infty}\frac{d t}{\sqrt{4t^3-g_2\;t-g_3}}$$ and so generalizing the answer to the original question for any integrand of the form $\frac{1}{\sqrt{R(t)}}$, where $R(t)$ is a fourth or a third order polynomial in $t$. This formula can be implemented in the following way:
z[ Dc_, OM_, OL_]:= WeierstrassP[ Sqrt[OM/4] Dc+ InverseWeierstrassP[ 1, { 0,-4OL/OM}], { 0, -4OL/OM}]-1
We rationalize numeric constants to play with the system seamlessly (although this step is not neccesary):
{ OM, OL} = Rationalize[{ OmegaM = 0.3111, OmegaLambda = 0.6889}];
Let's derive $z$: $$D_c=\int^{z}_{0}\frac{d s}{\sqrt{\Omega_M (s+1)^3+\Omega_{\Lambda}}}=\frac{2}{\sqrt{\Omega_M}}\int^{z+1}_{1}\frac{d s}{\sqrt{4 s^3+\frac{4\Omega_{\Lambda}}{\Omega_M}}}=\\=\frac{2}{\sqrt{\Omega_M}}\Bigg(\int^{\infty}_{1}\frac{d s}{\sqrt{4 s^3+\frac{4\Omega_{\Lambda}}{\Omega_M}}}-\int^{\infty}_{z+1}\frac{d s}{\sqrt{4 s^3+\frac{4\Omega_{\Lambda}}{\Omega_M}}}\Bigg)=\\=\frac{2}{\sqrt{\Omega_M}}\Bigg(-\wp^{-1}\big(1;0,-\frac{4\Omega_\Lambda}{\Omega_M}\big)+\wp^{-1}\big(z+1;0,-\frac{4\Omega_\Lambda}{\Omega_M}\big)\Bigg)$$ and this implies our formula for $z$.
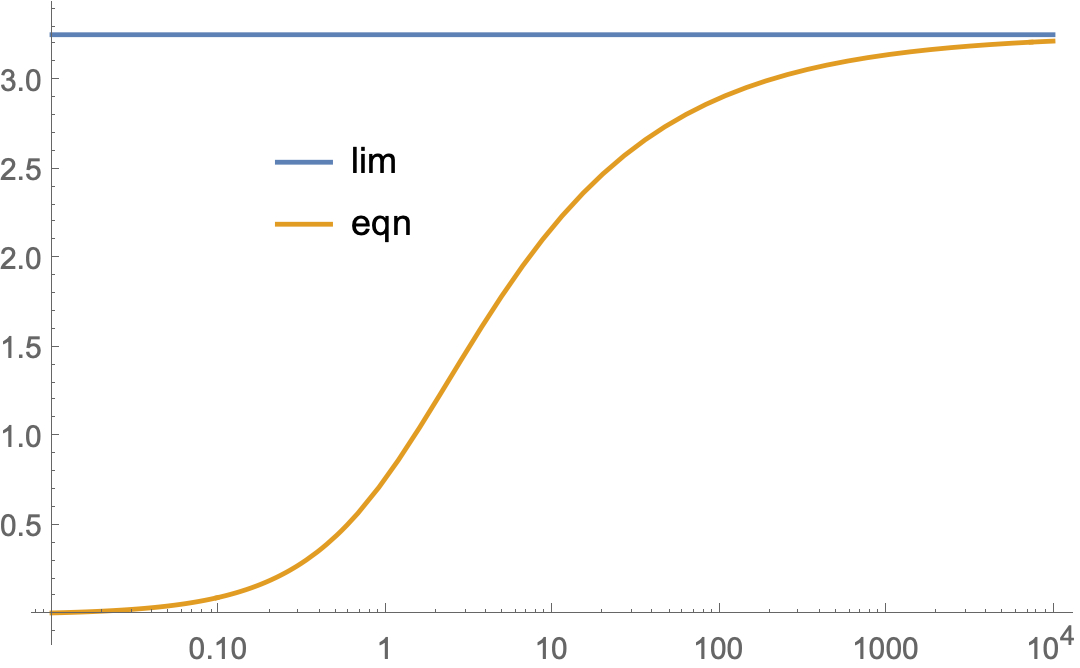
The formula for $z$ is valid in the range $0<D_c<D_{m}=3.25664$ and we can also derive an exact formula for $D_m$: $$D_m=\frac{2}{\sqrt{\Omega_M}} \Re\Big( 2\;\omega_{1}(0,g_3)-\wp^{-1}\big(1;0,g_3\big)\Big)$$ where $\Re$ is the real part, $\omega_{1}(0,g_3)$ is the Weierstrass half period and $g_3$ is the Weierstrass invariant, in our case $g_3=-\frac{4\Omega_{\Lambda}}{\Omega_M}$, implementing it:
g3=-4OL/OM; Dm = 2/Sqrt[OM]( 2WeierstrassHalfPeriodW1[{0, g3}]-InverseWeierstrassP[1,{0, g3}])//Re//N
3.25664
Dm been calculated in version 12.1, however in earlier versions one should evaluate simply Dm = -2/Sqrt[OM] InverseWeierstrassP[1,{0, g3}]. This is because InverseWeierstrassP[1,{0, g3}] is computed in a adjacent parallelogram (see e.g this discussion). One should also note better handling of symbolic input in WeierstrssHalfPeriodW1 etc. For the presentation of the structure of $z$ being an elliptic function (shifted and rescaled $\wp$) we define:
wHP = Through @ { WeierstrassHalfPeriodW1,WeierstrassHalfPeriodW2, WeierstrassHalfPeriodW3} @{ 0,-4OL/OM}//ReIm // FullSimplify; GraphicsRow @ Table[ ContourPlot[ Evaluate @ Table[p[z[x+I y,OM,OL]] ==k, {k, wHP[[#1,#2]]& @@@ {{2,1},{2,2},{3,1},{3,2}}}], {x, -8, 8}, {y, -8, 8}, ContourStyle ->Thread[ {Thick,{Red,Darker@Cyan,Darker@Green,Orange}}]], {p, {Re, Im}}]
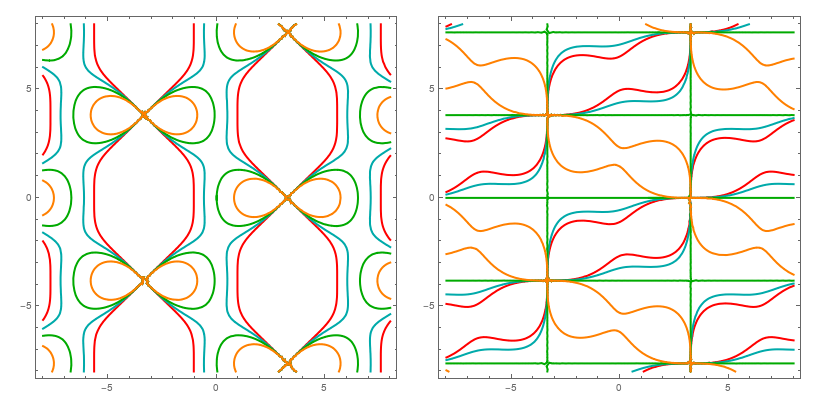
There was an assumption that $z>0$, however $D_c=500$ can be reached for negative $z$, e.g.
z[ 500,OM, OL]//N//Chop
-1.73134
and for $0< z<D_m$ e.g.
z[ 2, OM, OL]//N//Chop
7.13731