How to find the conformal mapping between two regions

We can use PI algorithm described in the paper Numerical Conformal Mapping with Rational Functions.The function for conformal mapping can be computed as follows

Needs["NDSolve`FEM`"]; reg1 = Triangle[{{2, 1}, {2, 3}, {0, 4}}]; reg2 = ImplicitRegion[x^2 + y^3 < 2 && y > x^2, {x, y}]; f[reg_, order_] := Module[{Z, A, B, eq, g, vec, mat, sol, R1, z1, bndedges, bndvertices, bpts, b, b0, aa, bb}, z1 = N@RegionCentroid[reg]; R1 = ToElementMesh[reg, "MaxBoundaryCellMeasure" -> .01, "MaxCellMeasure" -> .001]; bndedges = R1["BoundaryElements"][[1, 1]]; bndvertices = Sort@DeleteDuplicates[Flatten[bndedges]]; bpts = R1["Coordinates"][[bndvertices]]; b = ConstantArray[0., Length[R1["Coordinates"]]]; b0 = b[[ bndvertices]] = -0.5 Log[ Total[(bpts - ConstantArray[z1, Length[bpts]])^2, {2}]]; With[{nn = order}, Z = {x, y} |-> Table[ComplexExpand[(x + I y)^n], {n, 0, nn}]; A = Array[aa, {nn + 1}]; B = Array[bb, {nn + 1}]; g = {x, y} |-> ComplexExpand[(A + I B) . Z[x, y]]]; eq = -b0 + (g[#[[1]] - z1[[1]], #[[2]] - z1[[2]]] & /@ bpts) /. I -> 0; {vec, mat} = CoefficientArrays[Join[{bb[1]}, eq], Join[A, B]]; sol = LeastSquares[mat, -vec]; With[{nn = order}, Do[aa[i] = sol[[i]]; bb[i] = sol[[nn + 1 + i]];, {i, nn + 1}]]; {{x, y} |-> ReIm[Evaluate[ ComplexExpand[((x + I y) - (z1[[1]] + I z1[[2]])) Exp[ g[x - z1[[1]], y - z1[[2]]]]]]], {x, y} |-> ComplexExpand[(A + I B) . Z[x, y]], z1, R1}]; 

Example of usage

{f1, g1, z1, mesh1} = f[reg1, 32]; {Plot3D[Evaluate[g1[x - z1[[1]], y - z1[[2]]]] // Re, Element[{x, y}, reg1], ColorFunction -> Hue], Plot3D[Evaluate[g1[x - z1[[1]], y - z1[[2]]]] // Im, Element[{x, y}, reg1], ColorFunction -> Hue]} 

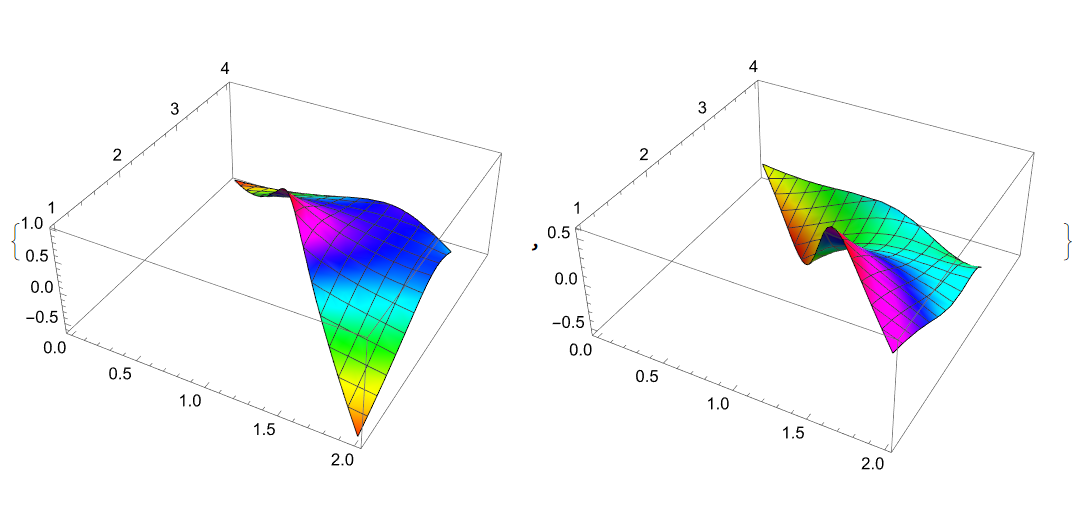
{f2, g2, z2, mesh2} = f[reg2, 32]; {Plot3D[Evaluate[g2[x - z2[[1]], y - z2[[2]]]] // Re, Element[{x, y}, reg2], ColorFunction -> Hue], Plot3D[Evaluate[g2[x - z2[[1]], y - z2[[2]]]] // Im, Element[{x, y}, reg2], ColorFunction -> Hue]} 

Mesh lines on reg2

rho2 = ContourPlot[Abs[f2[x, y]], Element[{x, y}, reg2], Contours -> Range[.1, .9, .1], ColorFunction -> Function[{x, y}, Hue[1/3, 1, 1, .5]], AspectRatio -> Automatic]; arg2 = ContourPlot[Arg[f2[x, y]], Element[{x, y}, reg2], Contours -> Pi Range[-.8, .8, .1], ColorFunction -> Function[{x, y}, Hue[1/3, 1, 1, .25]], AspectRatio -> Automatic, ExclusionsStyle -> Black]; Show[rho2, arg2] 

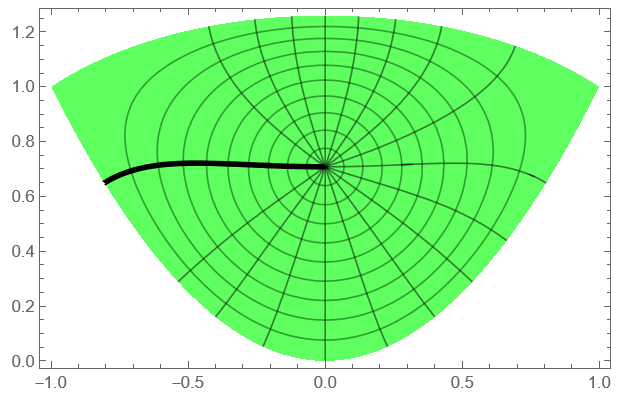
Mesh lines on reg1

rho1 = ContourPlot[Abs[f1[x, y]], Element[{x, y}, reg1], Contours -> Range[.1, .9, .1], ColorFunction -> Function[{x, y}, Hue[1/3, 1, 1, .5]], AspectRatio -> Automatic]; arg1 = ContourPlot[Arg[f1[x, y]], Element[{x, y}, reg1], ColorFunction -> Function[{x, y}, Hue[1/3, 1, 1, .25]], AspectRatio -> Automatic, Contours -> Pi Range[-.8, .8, .1], PlotPoints -> 50]; Show[rho1, arg1] 

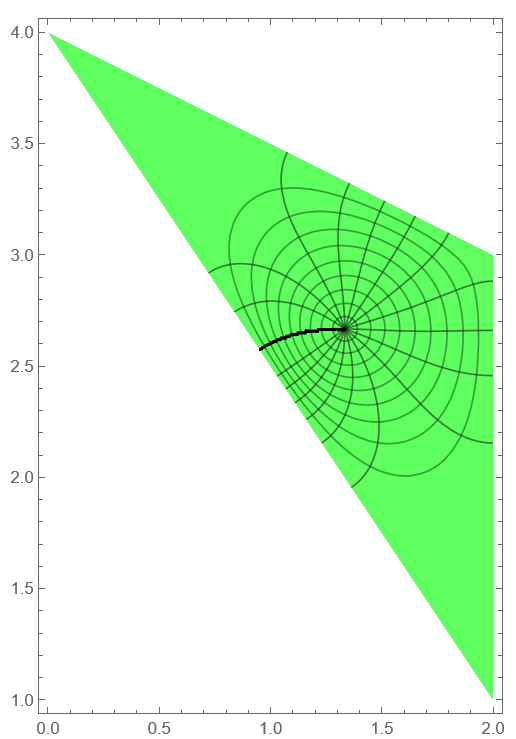
First attempt. We can try approach that recommended by yarchik and implemented by
Henrik Schumacher here. We have

Needs["NDSolve`FEM`"]; reg1 = Triangle[{{2, 1}, {2, 3}, {0, 4}}]; reg2 = ImplicitRegion[x^2 + y^3 < 2 && y > x^2, {x, y}]; f[reg_] := Module[{R, p, z0, ufun, vfun}, R = ToElementMesh[reg, "MeshOrder" -> 1, "MaxBoundaryCellMeasure" -> .01, "MaxCellMeasure" -> .001]; z0 = N@RegionCentroid[reg]; (*Initialization of Finite Element Method*) vd = NDSolve`VariableData[{"DependentVariables", "Space"} -> {{u}, {x, y}}]; sd = NDSolve`SolutionData[{"Space"} -> {R}]; cdata = InitializePDECoefficients[vd, sd, "DiffusionCoefficients" -> {{-IdentityMatrix[2]}}, "MassCoefficients" -> {{1}}]; bcdata = InitializeBoundaryConditions[vd, sd, {DirichletCondition[u[x, y] == 0., True]}]; mdata = InitializePDEMethodData[vd, sd]; (*Discretization*) dpde = DiscretizePDE[cdata, mdata, sd]; dbc = DiscretizeBoundaryConditions[bcdata, mdata, sd]; {load, stiffness, damping, mass} = dpde["All"]; DeployBoundaryConditions[{load, stiffness}, dbc]; (*Preparation of Dirichlet boundary conditions for u*) bndedges = R["BoundaryElements"][[1, 1]]; bndvertices = Sort@DeleteDuplicates[Flatten[bndedges]]; bpts = R["Coordinates"][[bndvertices]]; b = ConstantArray[0., Length[R["Coordinates"]]]; b[[bndvertices]] = -0.5 Log[ Total[(bpts - ConstantArray[z0, Length[bpts]])^2, {2}]]; (*Solving the system and creating an interpolating function*) solver = LinearSolve[stiffness, Method -> "Pardiso"]; uvals = solver[b]; ufun = ElementMeshInterpolation[{R}, uvals]; (*Preparation of Neumann boundary conditions for v*) gradu = {x, y} |-> Evaluate[D[ufun[x, y], {{x, y}, 1}]]; J = N@RotationMatrix[Pi/2]; p = R["Coordinates"]; {i, j} = Transpose[R["BoundaryElements"][[1, 1]]]; normalprojections = MapThreadDot[ R["BoundaryNormals"][[ 1]], (gradu @@@ (0.5 (p[[i]] + p[[j]]))) . (-J)]; boundaryedgelengts = Sqrt[Total[(p[[i]] - p[[j]])^2, {2}]]; {\[Alpha], \[Beta]} = Transpose[bndedges]; vertexbndedgeconnectivity = SparseArray[ Transpose[{Join[\[Alpha], \[Beta]], Join[Range[Length[\[Alpha]]], Range[Length[\[Beta]]]]}] -> 1, {Length[p], Length[bndedges]}]; (*Solving the system and creating an interpolating function*) b = vertexbndedgeconnectivity . (normalprojections \ boundaryedgelengts); vvals = solver[b]; vfun = ElementMeshInterpolation[{R}, vvals]; {x, y} |-> Evaluate[ ComplexExpand[ ReIm[((x + I y) - (z0[[1]] + I z0[[2]])) Exp[ ufun[x, y]] (Cos[vfun[x, y]] + I Sin[vfun[x, y]])]]]]; 

We use function f at reg1, reg2 as follows

f1 = f[reg1]; With[{R = ToElementMesh[reg1, "MeshOrder" -> 1, "MaxBoundaryCellMeasure" -> .01, "MaxCellMeasure" -> .001]}, p = R["Coordinates"]; tex = ColorData["BrightBands", "Image"]; texcoords = Transpose[{Total[(f1 @@@ p)^2, {2}], ConstantArray[0.5, Length[p]]}]; g1 = {Graphics[{Texture[tex], ElementMeshToGraphicsComplex[R, VertexTextureCoordinates -> texcoords]}, PlotRange -> All], Graphics[{Texture[tex], ElementMeshToGraphicsComplex[R, VertexTextureCoordinates -> texcoords, "CoordinateConversion" -> (f1 @@@ # &)]}]}] 

f2 = f[reg2]; With[{R = ToElementMesh[reg2, "MeshOrder" -> 1, "MaxBoundaryCellMeasure" -> .01, "MaxCellMeasure" -> .001]}, p = R["Coordinates"]; tex = ColorData["BrightBands", "Image"]; texcoords = Transpose[{Total[(f2 @@@ p)^2, {2}], ConstantArray[0.5, Length[p]]}]; g1 = {Graphics[{Texture[tex], ElementMeshToGraphicsComplex[R, VertexTextureCoordinates -> texcoords]}, PlotRange -> All], Graphics[{Texture[tex], ElementMeshToGraphicsComplex[R, VertexTextureCoordinates -> texcoords, "CoordinateConversion" -> (f2 @@@ # &)]}]}] 

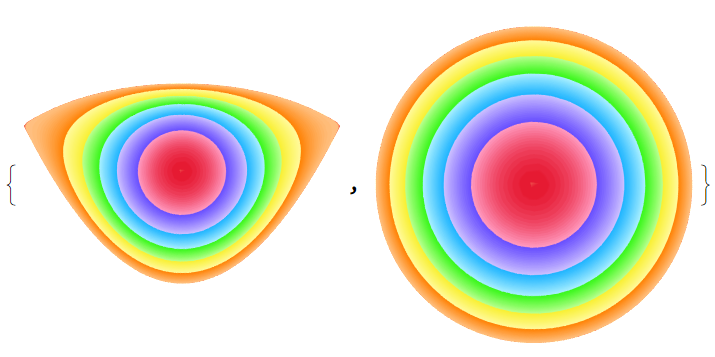
Nothing new above, but now we can map reg2 to reg1 using FindRoot

z0 = N@RegionCentroid[reg2]; ps = Sort[p, Norm[# - z0] &]; ds = f2[#[[1]], #[[2]]] & /@ ps; z1 = N@RegionCentroid[reg1]; ps1 = Table[{x, y} /. Quiet@FindRoot[ f1[x, y] == ds[[i]], {x, z1[[1]]}, {y, z1[[2]]}], {i, Length[ds]}]; 

Visualization

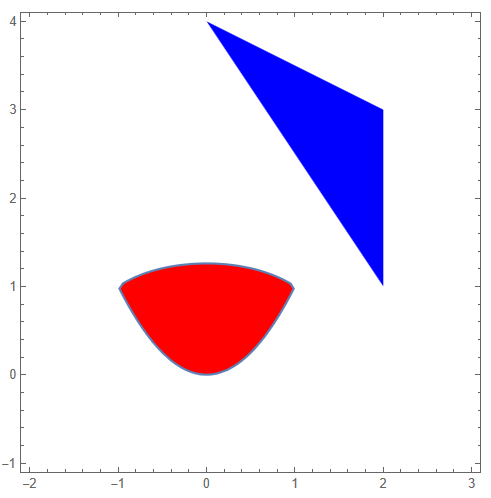
kmax = First[Last[Length[ps] // FactorInteger]]; nmax = Length[ps]/kmax; {ListPlot[ Table[Take[ps, {kmax i + 1, kmax (i + 1)}], {i, 0, nmax - 1}], PlotStyle -> cl], ListPlot[ Table[Take[ps1, {kmax i + 1, kmax (i + 1)}], {i, 0, nmax - 1}], AspectRatio -> 1, PlotStyle -> cl, PlotLegends -> Automatic]} 

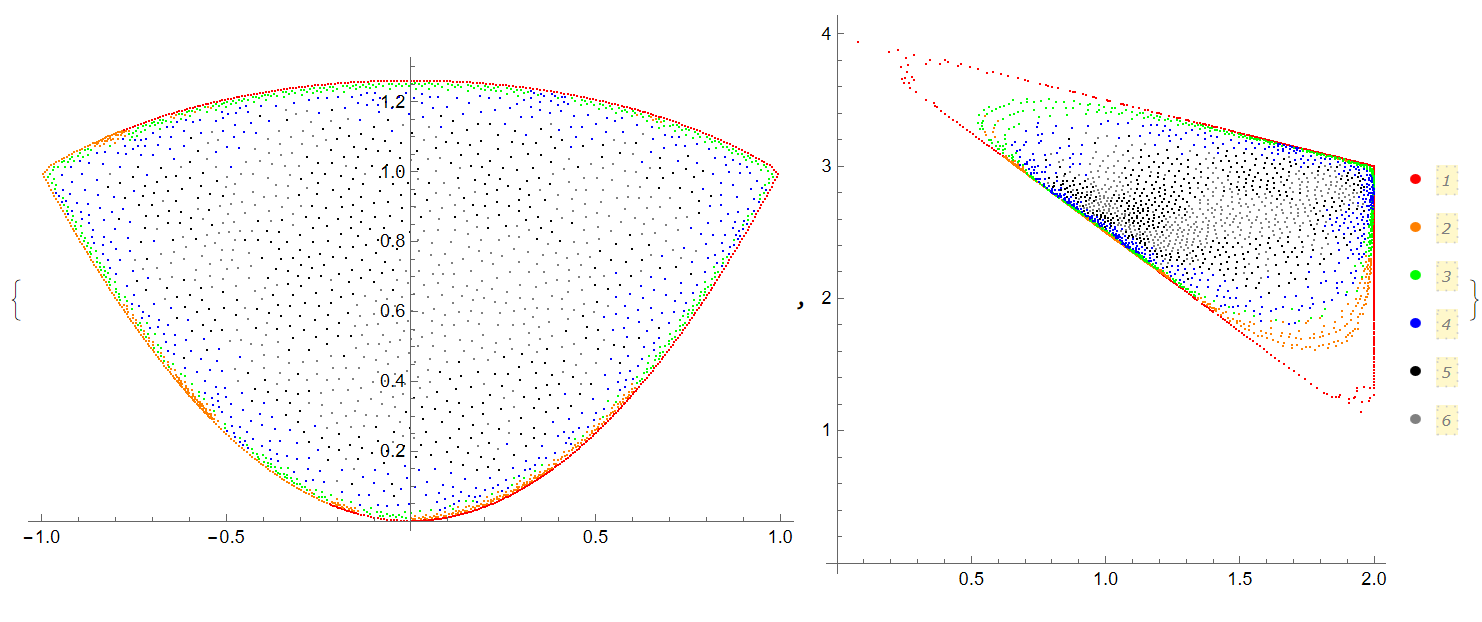
We also can check how parts of reg2 map at reg

cl = {Red, Orange, Green, Blue, Black, Gray}; Table[{ListPlot[Take[ps, {kmax i + 1, kmax (i + 1)}], PlotStyle -> cl[[i + 1]]], ListPlot[Take[ps1, {kmax i + 1, kmax (i + 1)}], AspectRatio -> 1, PlotStyle -> cl[[i + 1]]]}, {i, 0, nmax - 1}] 

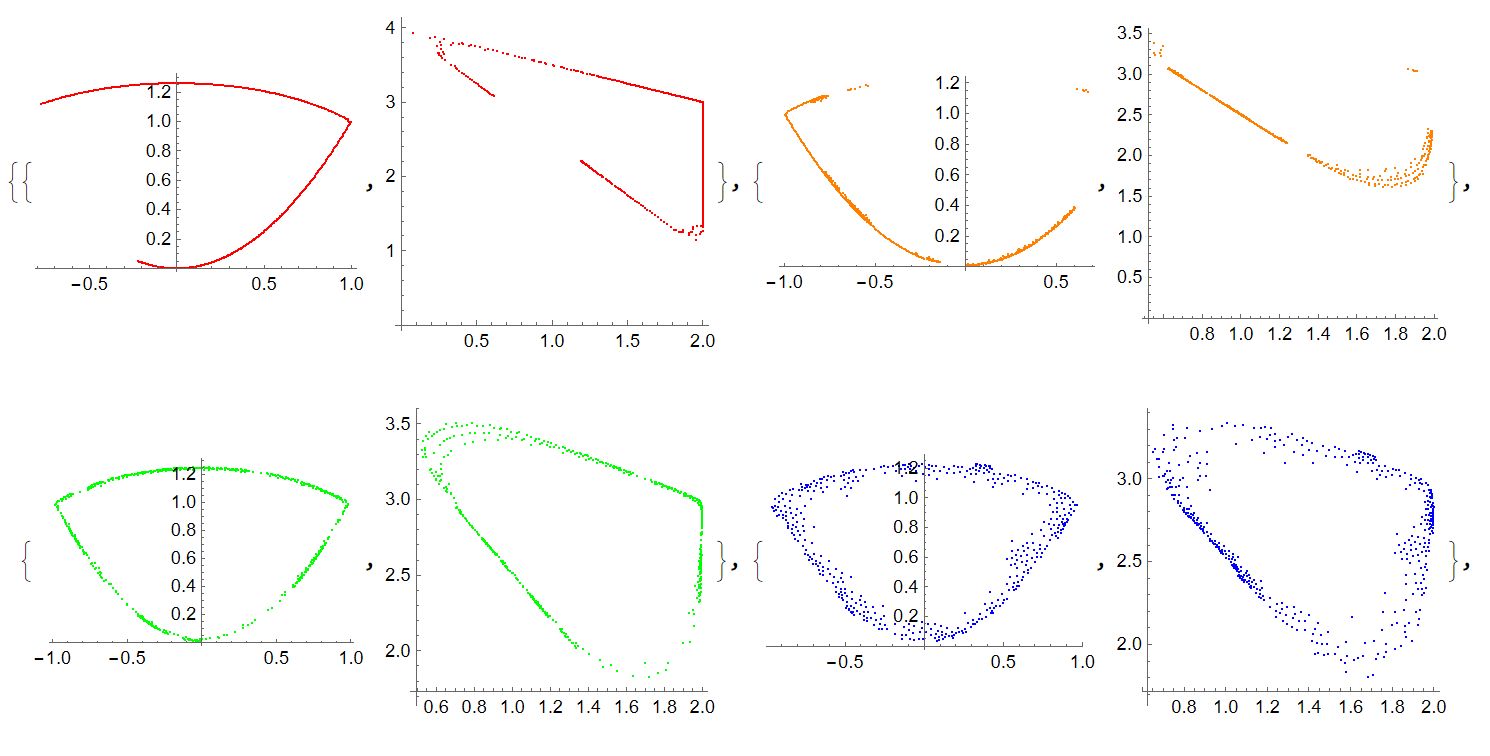
Update 1. Given the pictures that the user cvgmt provided us (thanks to him), we need to check how Schumacher's code calculates the functions ufun, vfun. For this we used NDSolve and our code with PI algorithm implemented in it - see paper Numerical Conformal Mapping with Rational Functions. NDSolve code is very simple

Needs["NDSolve`FEM`"]; reg1 = Triangle[{{2, 1}, {2, 3}, {0, 4}}]; reg2 = ImplicitRegion[x^2 + y^3 < 2 && y > x^2, {x, y}]; z1 = N@RegionCentroid[reg1]; R1 = ToElementMesh[reg1, "MaxBoundaryCellMeasure" -> .01, "MaxCellMeasure" -> .001]; U1 = NDSolveValue[{-Laplacian[u[x, y], {x, y}] == 0, DirichletCondition[ u[x, y] == -.5 Log[(x - z1[[1]])^2 + (y - z1[[2]])^2], True]}, u, Element[{x, y}, R1]]; Plot3D[U1[x, y], Element[{x, y}, reg1], ColorFunction -> Hue] 

The PI algorithm is based on the series expansion of a function $g(z)=u(z)+i v(z)$, where $\nabla^2 u=0$ with the Dirichlet condition $u=-\ln|z-z1|$. To compute $u,v$ we use mesh R1 generated above:

bndedges = R1["BoundaryElements"][[1, 1]]; bndvertices = Sort@DeleteDuplicates[Flatten[bndedges]]; bpts = R1["Coordinates"][[bndvertices]]; b = ConstantArray[0., Length[R1["Coordinates"]]]; b0 = b[[bndvertices]] = -0.5 Log[ Total[(bpts - ConstantArray[z1, Length[bpts]])^2, {2}]]; With[{nn = 32}, Z = {x, y} |-> Table[ComplexExpand[(x + I y)^n], {n, 0, nn}]; A = Array[aa, {nn + 1}]; B = Array[bb, {nn + 1}]; g = {x, y} |-> ComplexExpand[(A + I B) . Z[x, y]]]; eq = -b0 + (g[#[[1]] - z1[[1]], #[[2]] - z1[[2]]] & /@ bpts) /. I -> 0; {vec, mat} = CoefficientArrays[Join[{bb[1]}, eq], Join[A, B]]; sol = LeastSquares[mat, -vec]; With[{nn = 32}, Do[aa[i] = sol[[i]]; bb[i] = sol[[nn + 1 + i]];, {i, nn + 1}]]; 

Now we can compare U1 computed with NDSolve, ufun computed with Henrik Schumacher code (function f above), and function u=Re[g[z-z1]]

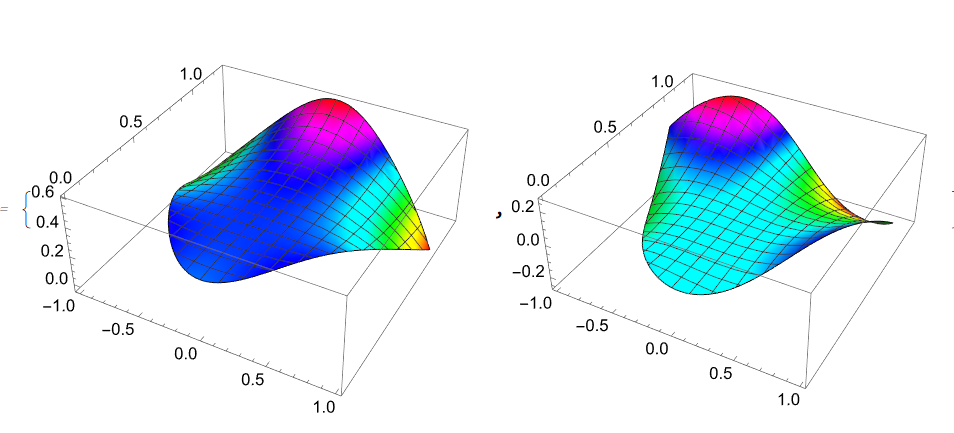
{Plot3D[U1[x, y], Element[{x, y}, reg1], ColorFunction -> Hue], Plot3D[ufun[x, y], Element[{x, y}, reg1], ColorFunction -> Hue], Plot3D[Evaluate[g[x - z1[[1]], y - z1[[2]]]] // Re, Element[{x, y}, reg1], ColorFunction -> Hue]} 

Fortunately all 3 functions look same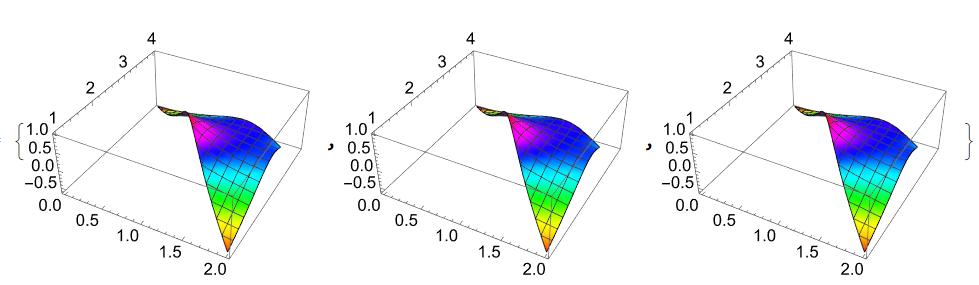

But unfortunately functions vfun and Im[g[z-z1]] are differ

{Plot3D[vfun[x, y], Element[{x, y}, reg1], ColorFunction -> Hue], Plot3D[Evaluate[g[x - z1[[1]], y - z1[[2]]]] // Im, Element[{x, y}, reg1], ColorFunction -> Hue]} 

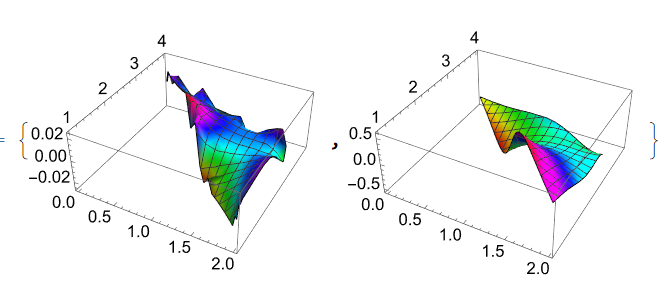Using g[z] computed above we can define conformal mapping reg1 on the unit disk as follows

f1p = {x, y} |-> ReIm[Evaluate[ ComplexExpand[((x + I y) - (z1[[1]] + I z1[[2]])) Exp[ g[x - z1[[1]], y - z1[[2]]]] ]]]; 

Finally we test f1p using code provided by cvgmt

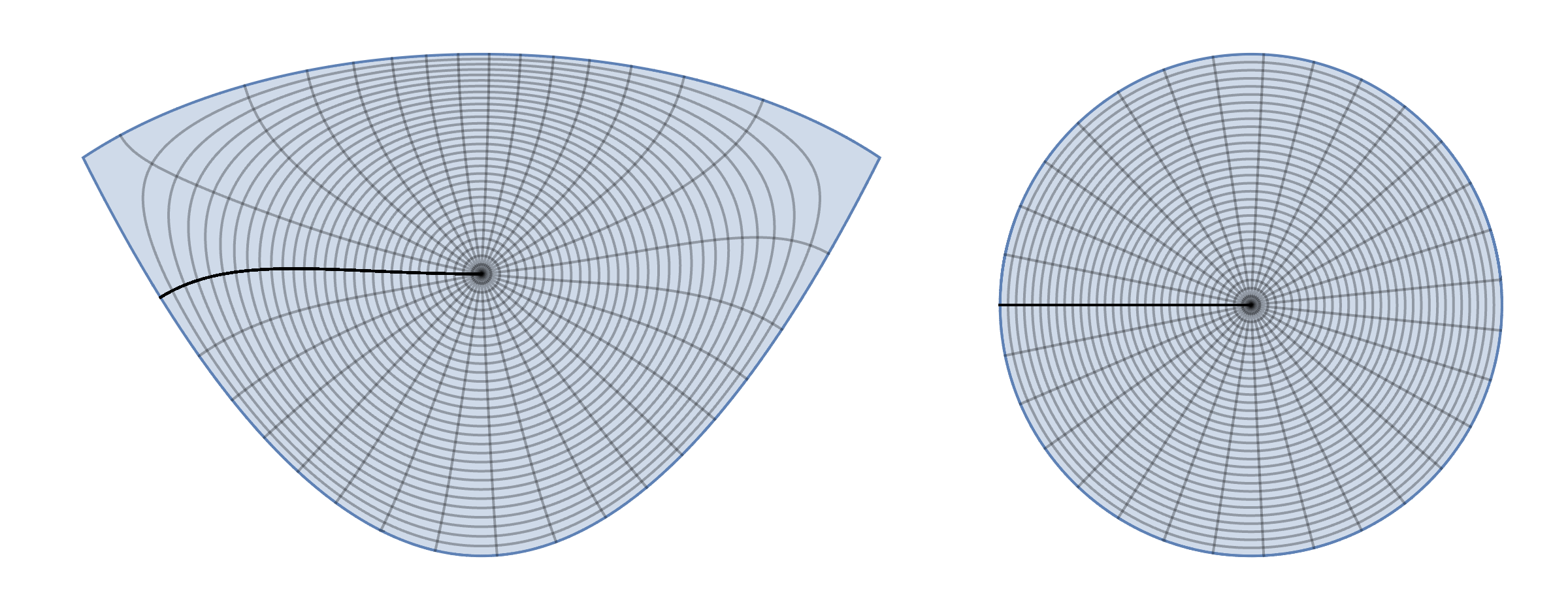
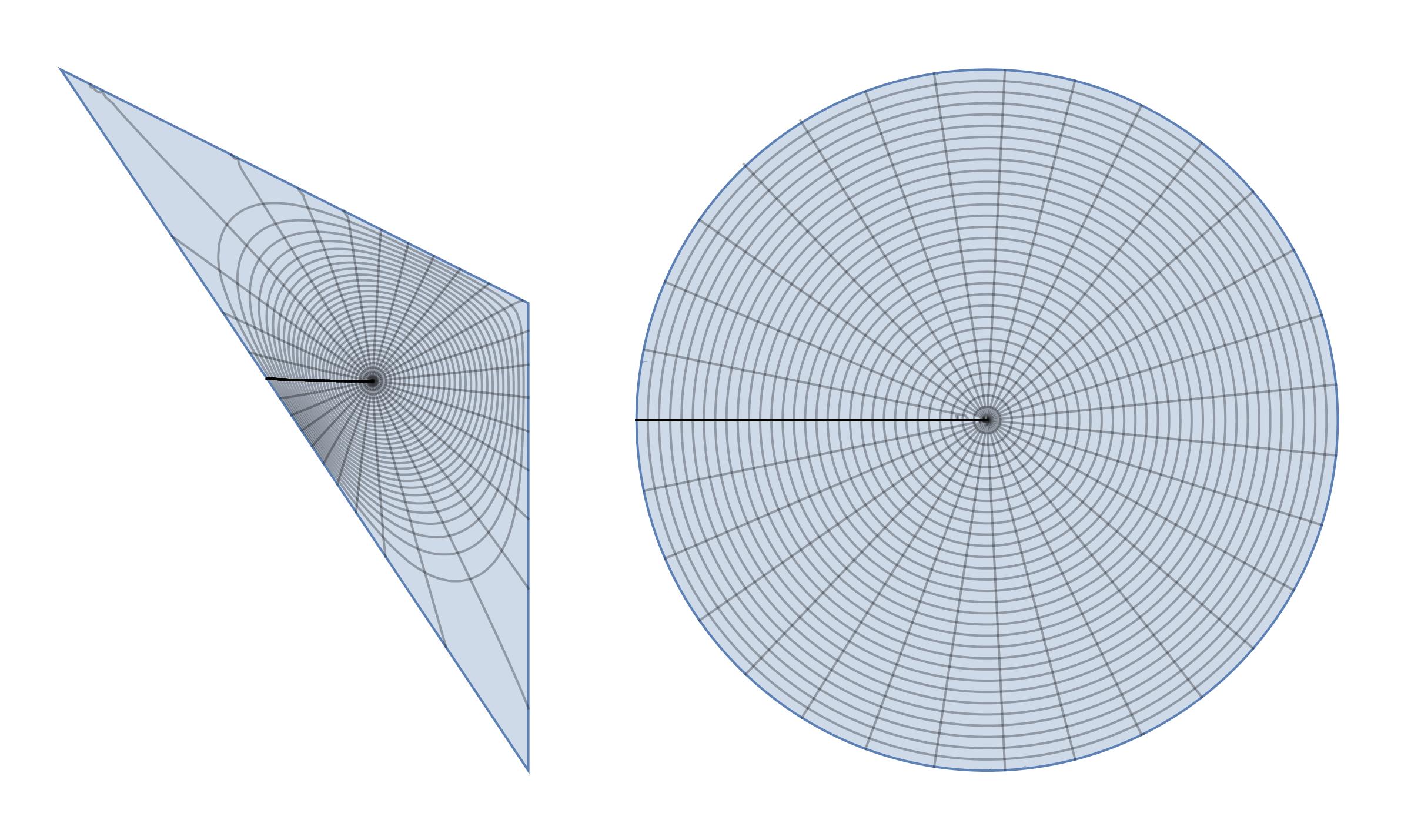
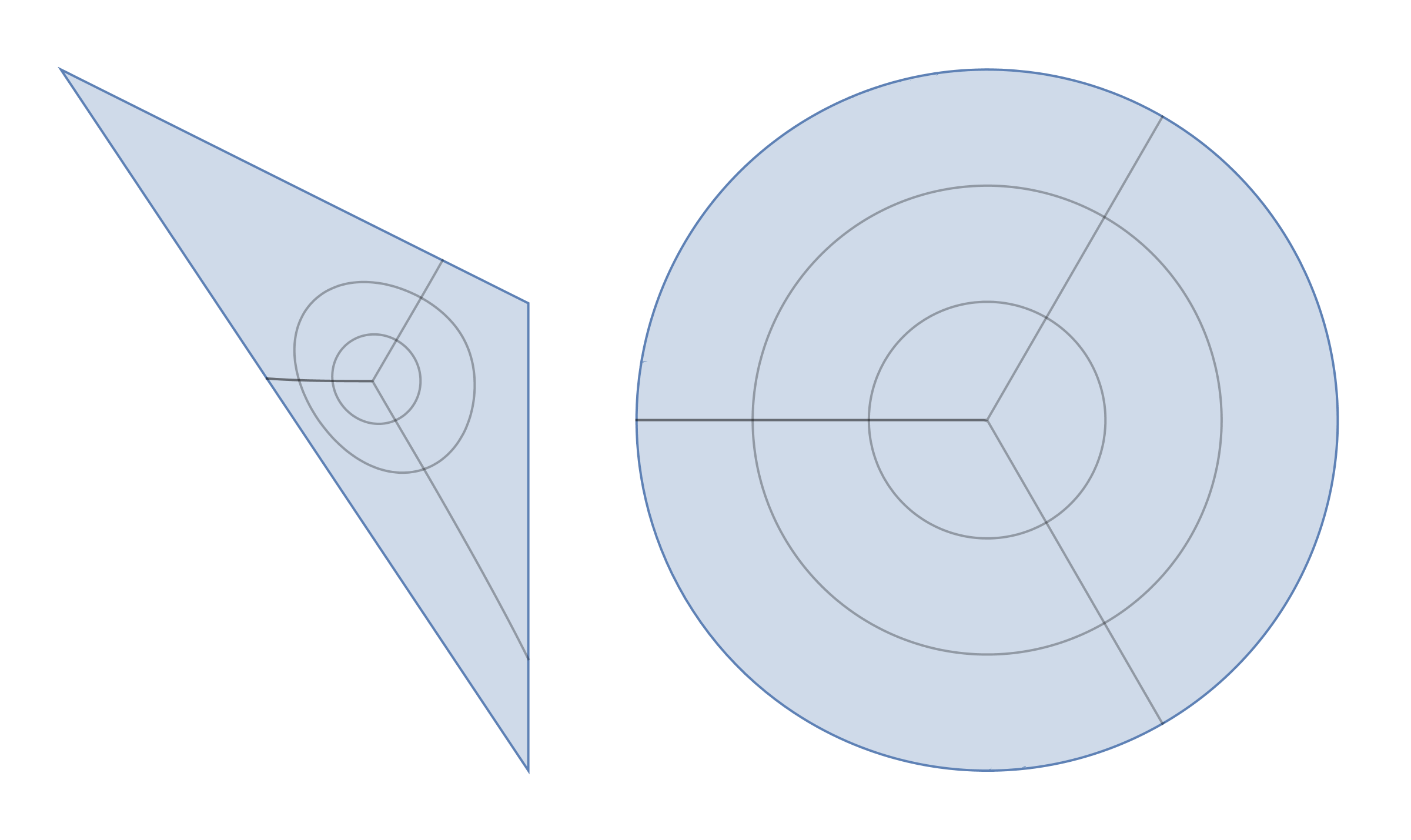
disktoreg1 = ParametricPlot[{x, y}, {x, y} \[Element] reg1, MeshFunctions -> {Function[{x, y}, Norm@{Indexed[f1p[x, y], 1], Indexed[f1p[x, y], 2]}], Function[{x, y}, ArcTan @@ {Indexed[f1p[x, y], 1], Indexed[f1p[x, y], 2]}]}, Frame -> False, Axes -> False, Mesh -> {30, 30}]; reg1todisk = ParametricPlot[f1p[x, y], {x, y} \[Element] reg1, MeshFunctions -> {Function[{x, y}, Norm@{x, y}], Function[{x, y}, ArcTan @@ {x, y}]}, Frame -> False, Axes -> False, Mesh -> {30, 30}]; GraphicsRow[{disktoreg1, reg1todisk}] 

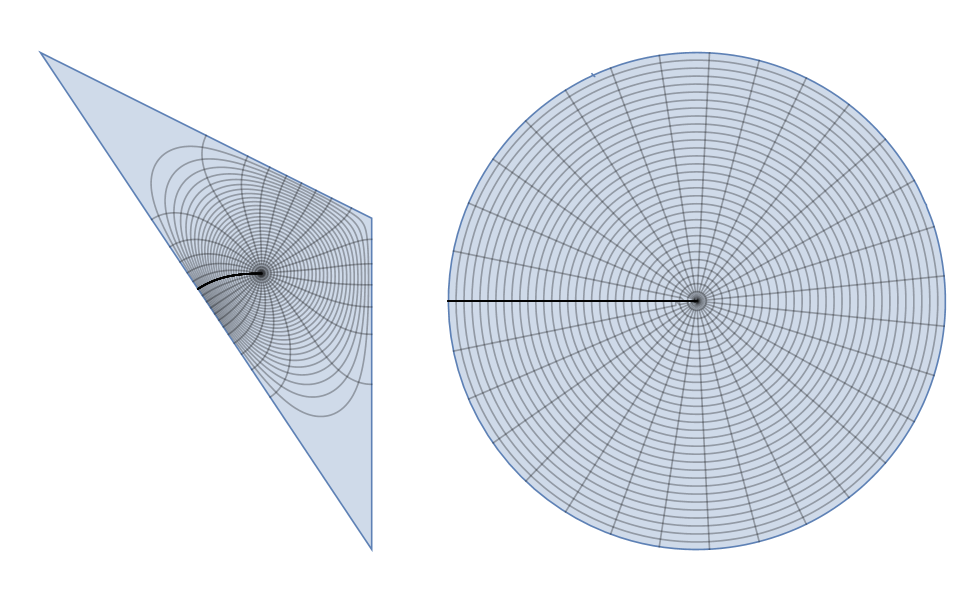
Now it looks like conformal map since all grid lines are orthogonal.
It is clear that function vfun computed with higher error and we need to improve code for f. On the other hand we can use more simple approach based on PI algorithm.

The result of the reg2.

Updated

• We use schwarz christoffel formula for triangle. $$ \int_{0}^{z} (\zeta-a_1)^{\alpha_1-1} (\zeta-a_1)^{\alpha_2-1}\,\mathrm{d}\zeta$$

• To integrate such integral, we set Assumptions -> {Im[z] > 0} since we mapping the upper plane to the triangle.

• And we use (z - (u + I*v))/(z - (u - I*v)) mapping the upper plane to the disk and find its inversion.

• The final mapping is the disk to triangle.

Clear["Global`*"]; a1 = 0; a2 = 1; a3 = ∞; {a, b, c} = {{2, 1}, {2, 3}, {0, 4}}; (*{a,b,c}=RandomPolygon[3][[1]];*) {w1, w2, w3} = {a, b, c} . {1, I}; center0 = Mean[{a, b, c}]; center = center0 . {1, I}; tri = Triangle[{a, b, c}]; {α1, α2, α3} = {VectorAngle[b - a, c - a], VectorAngle[c - b, a - b], VectorAngle[a - c, b - c]}/π; f[z_] = A + B*Simplify[ Integrate[(ζ - a1)^(α1 - 1) (ζ - a2)^(α2 - 1), {ζ, 0, z}, Assumptions -> {Im[z] > 0}]]; sol = NSolve[{f[a1] == w1, f[a2] == w2}]; F[z_] = f[z] /. sol[[1]]; {F[a1], F[a2], Limit[F[t], t -> ∞]} == {w1, w2, w3}; (*True*) sol1 = z /. FindRoot[F[z] == center, {z, 1}][[1]] // ReIm; disk2upper[ w_] = (z /. Solve[(z - (u + I*v))/(z - (u - I*v)) == w, z][[1]]) /. Thread[{u, v} -> sol1]; (*ParametricPlot[ReIm[disk2upper[x+I*y]]//Evaluate,{x,y}∈\ Disk[{0,0},1-10^-10],Mesh->30]*) disk2triangle[x_, y_] = ReIm[F@disk2upper[x + I*y]]; g1 = {ParametricPlot[ disk2triangle[x, y], {x, y} ∈ BoundaryDiscretizeRegion@Disk[{0, 0}, 1 - 10^-10], PlotStyle -> None, BoundaryStyle -> None, MeshFunctions -> {Norm@{#3, #4} &, ArcTan @@ {#3, #4} &}, Mesh -> 30, MeshShading -> {{White, Black}, {Black, White}}, PlotPoints -> 60, MaxRecursion -> 2, BoundaryStyle -> Black, PlotRange -> All, Frame -> False, Axes -> False], Graphics[{FaceForm[], EdgeForm[Black], tri}]} // Show; g2 = {ParametricPlot[{x, y}, {x, y} ∈ BoundaryDiscretizeRegion@Disk[{0, 0}, 1 - 10^-10], PlotStyle -> None, BoundaryStyle -> None, MeshFunctions -> {Norm@{#3, #4} &, ArcTan @@ {#3, #4} &}, Mesh -> 30, MeshShading -> {{White, Black}, {Black, White}}, PlotPoints -> 60, MaxRecursion -> 2, BoundaryStyle -> Black, PlotRange -> All, Frame -> False, Axes -> False], Graphics[{FaceForm[], EdgeForm[Black], Circle[]}]} // Show; GraphicsRow[{g1, g2}] 

• test the inverse, maybe not so corrected.

(* the polar coordinate of triangle to disk*) G2 = ParametricPlot[{x, y}, {x, y} ∈ Disk[{0, 0}, 1 - 10^-10], MeshFunctions -> {Function[{x, y}, Norm@{Indexed[disk2triangle[x, y], 1] - center0[[1]], Indexed[disk2triangle[x, y], 2] - center0[[2]]}], Function[{x, y}, ArcTan @@ {Indexed[disk2triangle[x, y], 1] - center0[[1]], Indexed[disk2triangle[x, y], 2] - center0[[2]]}]}, Frame -> False, Axes -> False, Mesh -> 30, MeshShading -> {{White, Black}, {Black, White}}]; G1 = ParametricPlot[{x, y}, {x, y} ∈ tri, PlotStyle -> None, BoundaryStyle -> None, MeshFunctions -> {Norm[{#3, #4} - center0] &, ArcTan @@ ({#3, #4} - center0) &}, Mesh -> 30, MeshShading -> {{White, Black}, {Black, White}}, PlotPoints -> 60, MaxRecursion -> 2, BoundaryStyle -> Black, PlotRange -> All, Frame -> False, Axes -> False]; GraphicsRow[{G1, G2}] 

Original

• Not an answer.
• Here we draw the polar coordinate orthogrnal lines on Disk[] and map to reg1. We found that the f1 seems not preserve the angle of orthogrnal lines. ( it means 90 Degree)
• The f1=f[reg1] where f in the answer of @AlexTrounev https://mathematica.stackexchange.com/a/297116/72111 or the f1 is equal to the f in the answer of @HenrikSchumacher https://mathematica.stackexchange.com/a/178333/72111 when we replace R with reg1.

f1 = f[reg1]; disktoreg1 = ParametricPlot[{x, y}, {x, y} ∈ reg1, MeshFunctions -> {Function[{x, y}, Norm@{Indexed[f1[x, y], 1], Indexed[f1[x, y], 2]}], Function[{x, y}, ArcTan @@ {Indexed[f1[x, y], 1], Indexed[f1[x, y], 2]}]}, Frame -> False, Axes -> False, Mesh -> {30, 30}]; reg1todisk = ParametricPlot[f1[x, y], {x, y} ∈ reg1, MeshFunctions -> {Function[{x, y}, Norm@{x, y}], Function[{x, y}, ArcTan @@ {x, y}]}, Frame -> False, Axes -> False, Mesh -> {30, 30}]; GraphicsRow[{disktoreg1, reg1todisk}] 

• We check two mesh lines Mesh -> 2.