4
$\begingroup$

Can you make the code for tangent line and normal line of implicit algebraic curve cu more concise than mine?

The code for tangent line at {x,y}={8,7} is:

D[cu, {{x, y}}] . {a - x, b - y} /. {x -> 8, y -> 7} /. {a -> x, b -> y} // Expand

The code for normal line at {x,y}={8,7} is:

D[cu, {{y, x}}] . {a - x, -b + y} /. {x -> 8, y -> 7} /. {a -> x, b -> y} // Expand

What I do not like about my code is that it uses two Rule's and two temporary and meaningless variables a, b.

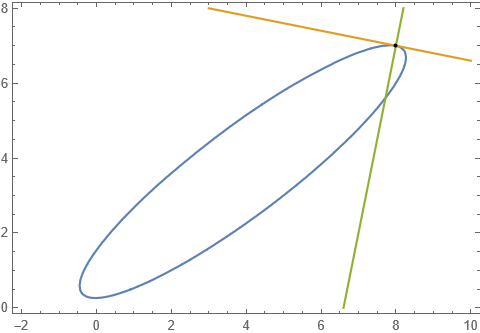
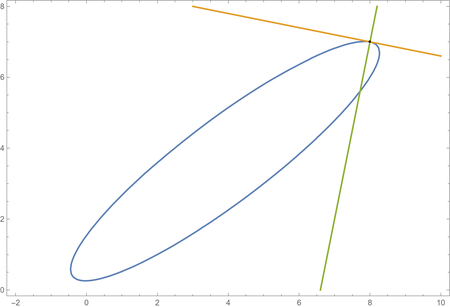
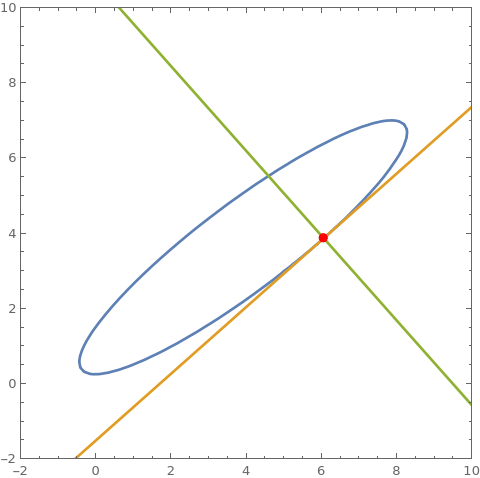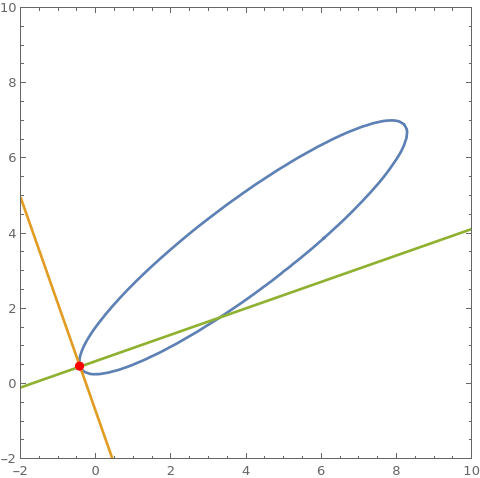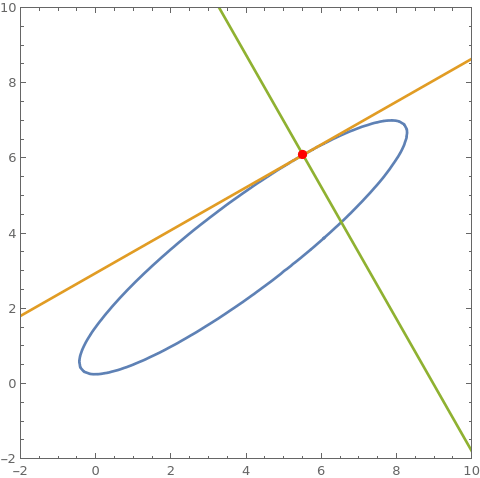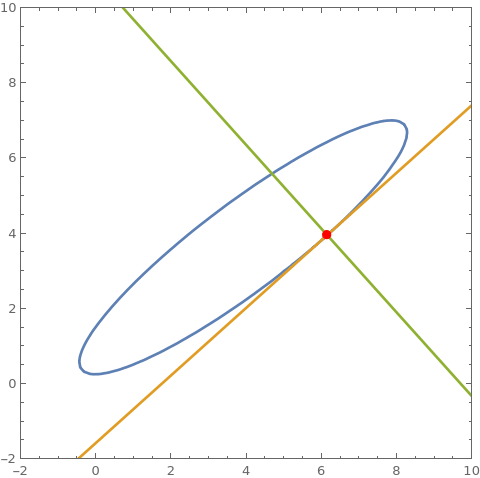
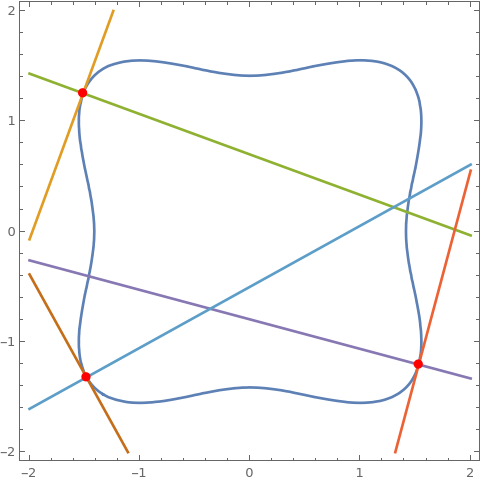
cu = 3 x^2 + 5 y^2 - 7 x y + 2 x - 9 y + 2; cu == 0 /. {x -> 8, y -> 7} D[cu, {{x, y}}] . {a - x, b - y} /. {x -> 8, y -> 7} /. {a -> x, b -> y} // Expand D[cu, {{y, x}}] . {a - x, -b + y} /. {x -> 8, y -> 7} /. {a -> x, b -> y} // Expand ContourPlot[{cu == 0, %% == 0, % == 0}, {x, -2, 10}, {y, 0, 8}, Epilog -> {Point[{8, 7}]}, AspectRatio -> Automatic] Clear[cu] (* True *) (* -43 + x + 5 y *) (* -33 + 5 x - y *)

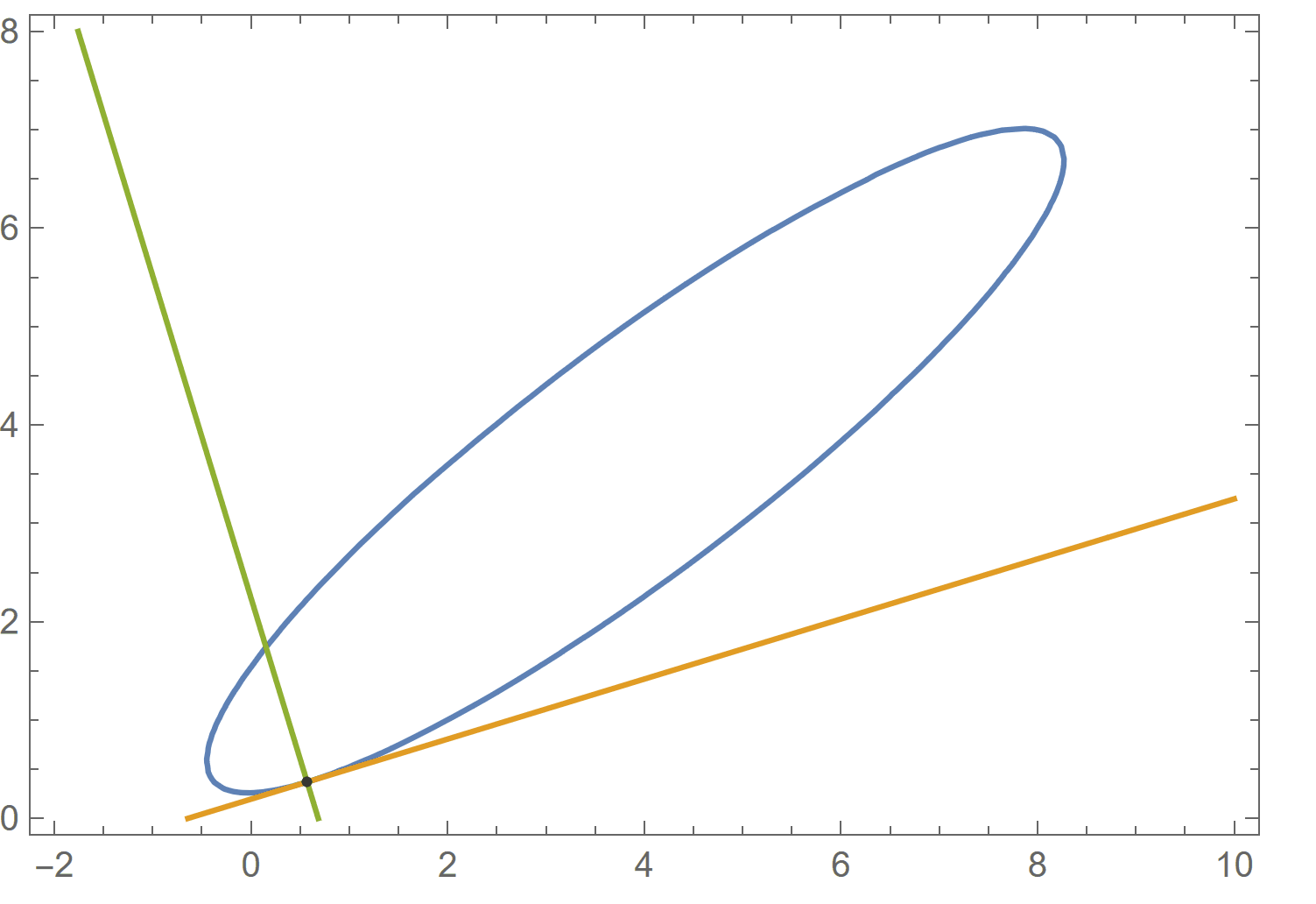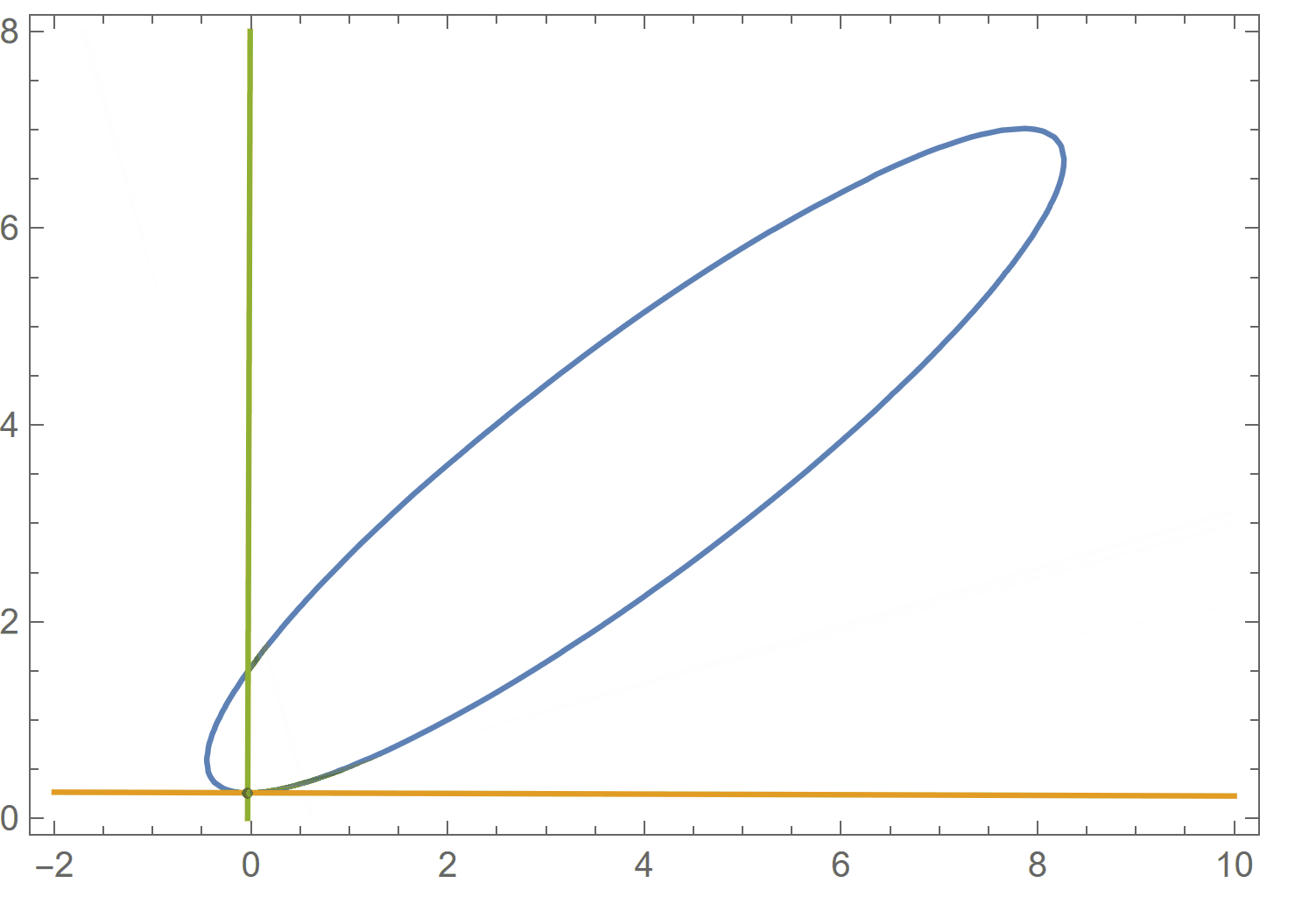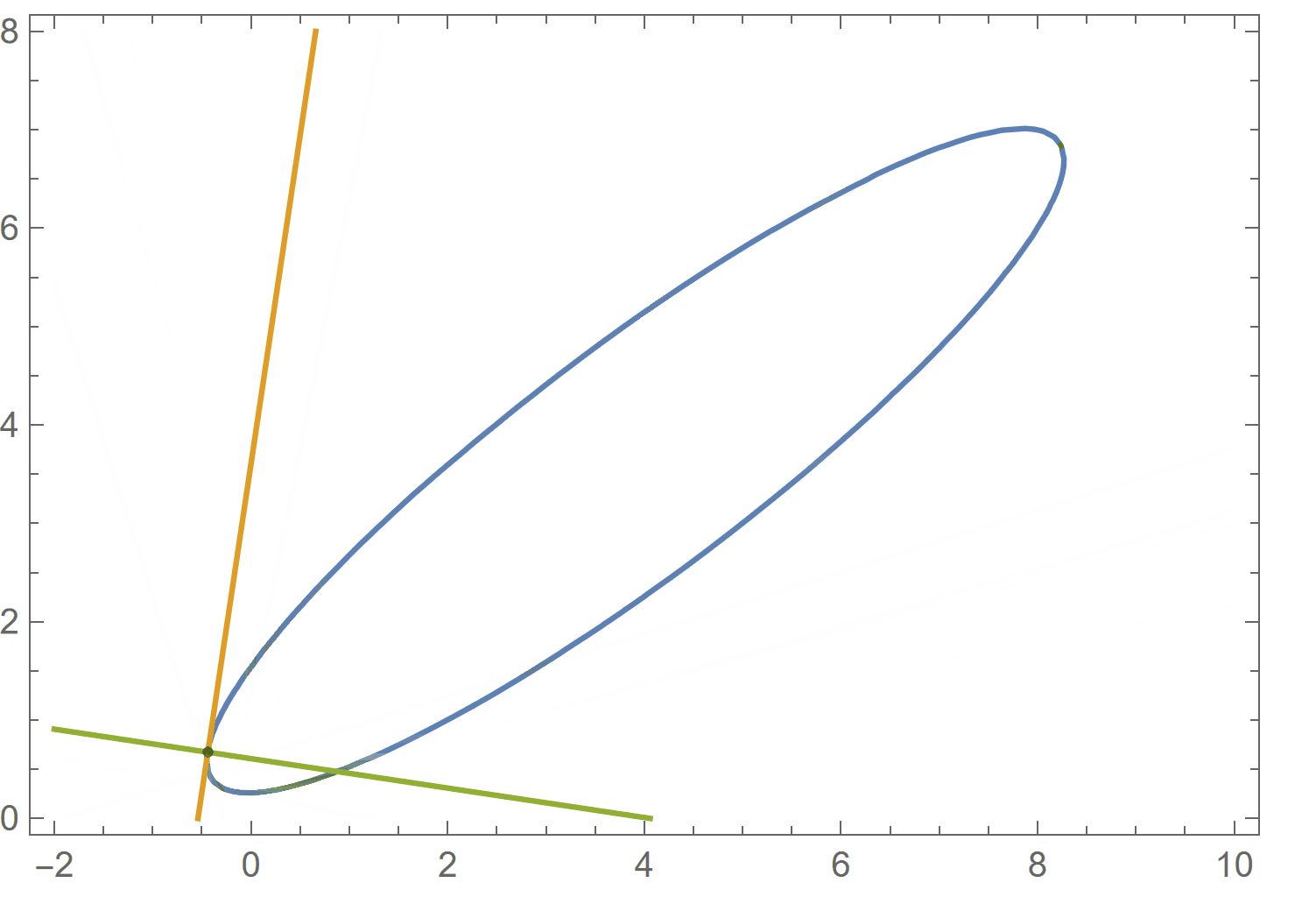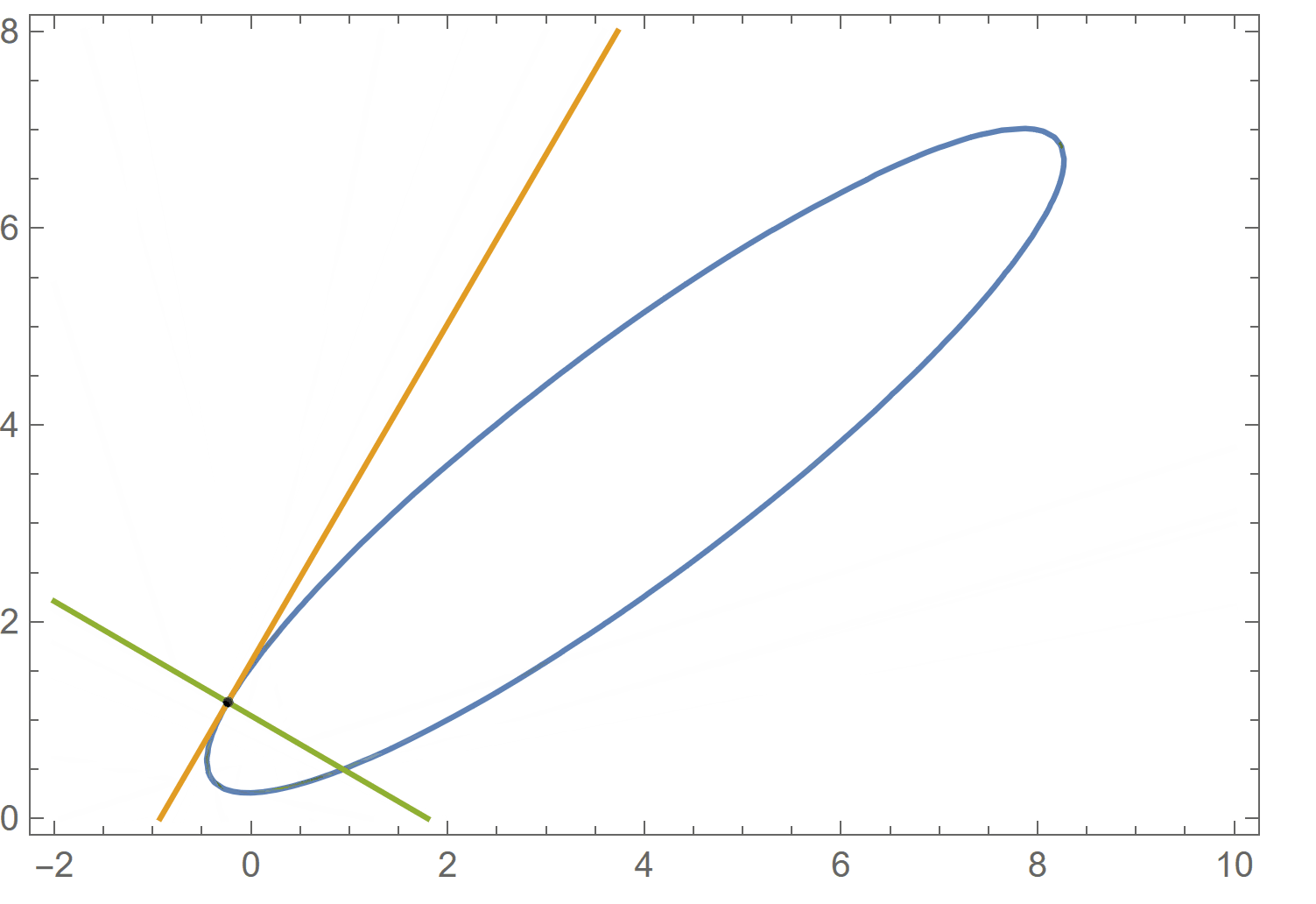
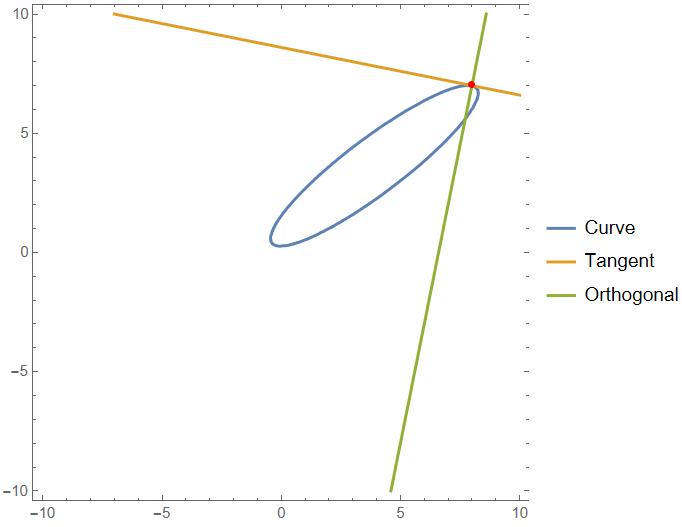
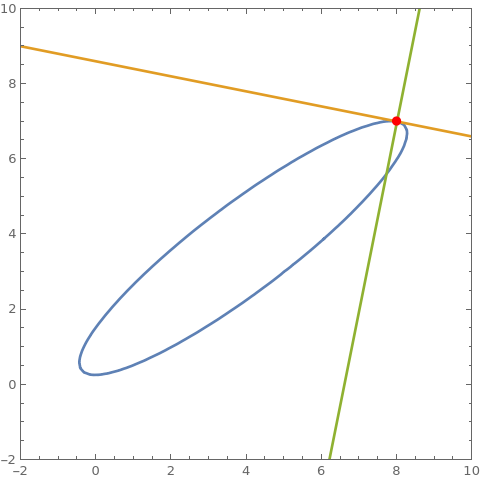
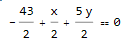
enter image description here

Improve this question
$\endgroup$
3
  • $\begingroup$ {x,y} is on the curve cu and {X,Y} is on the tangen line. D[cu, {{x, y}}] . ({X, Y} - {x, y}) /. {x -> 8, y -> 7} // Expand $\endgroup$ Commented Sep 30, 2023 at 15:45
  • $\begingroup$ It is the same as mine you just renamed variables and the result tangent is in X, Y which you have to replace by another rule to have it in desired x, y variables. $\endgroup$ Commented Sep 30, 2023 at 15:50
  • $\begingroup$ For example, I always use Y==((f[x]-f[x0])/(x-x0))*(X-x0)+f[x0] to express a line which passes through the point {x0,f[x0]} and {x,f[x]}. {x,y} is on the curve {x,f[x]} and {X,Y} is on the line. $\endgroup$ Commented Sep 30, 2023 at 15:59

5 Answers 5

Reset to default
6
$\begingroup$
  • For the curve f[x,y]==0, we use
grad = Through@*Apply[{Derivative[1, 0][f], Derivative[0, 1][f]}];

to define a Grad operator to calculus the normal of implicit curve f[x,y]==0 on the point pt={a,b}={8,7}.

Clear["Global`*"]; f[x_, y_] := 3 x^2 + 5 y^2 - 7 x y + 2 x - 9 y + 2; rotation = RotationTransform[π/2]; grad = Through@*Apply[{Derivative[1, 0][f], Derivative[0, 1][f]}]; pt = {8, 7}; ContourPlot[{f[x, y] == 0, grad@{a, b} . {x - a, y - b} == 0, rotation@grad@{a, b} . {x - a, y - b} == 0} /. Thread[{a, b} -> pt] // Evaluate, {x, -2, 10}, {y, 0, 8}, Epilog -> {Point[pt]}, AspectRatio -> Automatic]

enter image description here

  • animation.
plot = ContourPlot[f[x, y] == 0, {x, -2, 10}, {y, 0, 8}]; pts = Cases[plot, GraphicsComplex[pts_, data__] :> pts, -1] // First; data = Table[ ContourPlot[{f[x, y] == 0, grad@pt . ({x, y} - pt) == 0, rotation@grad@pt . ({x, y} - pt) == 0} // Evaluate, {x, -2, 10}, {y, 0, 8}, Epilog -> {Point[pt]}, AspectRatio -> Automatic], {pt, pts}]; ani = ListAnimate[data]

enter image description here

Improve this answer
$\endgroup$
5
$\begingroup$

You can useDt. For example for curve cu:

cu = 3 x^2 + 5 y^2 - 7 x y + 2 x - 9 y + 2;

you can do:

tn[f_, p_] := Module[{td = Dt[f], t, n, ex1, ex2}, t = td /. {Dt[x] -> {1, 0}, Dt[y] -> {0, 1}}; n = td /. {Dt[x] -> {0, 1}, Dt[y] -> {-1, 0}}; ex1 = (t /. Thread[{x, y} -> p]) . ({x, y} - p); ex2 = (n /. Thread[{x, y} -> p]) . ({x, y} - p); Column[{ContourPlot[{f == 0, ex1 == 0, ex2 == 0}, {x, -2, 10}, {y, -2, 10}, Epilog -> {Red, Point[p]}], Grid[{{"curve", f == 0}, {StringForm["tangent at ``", p], ex1 == 0}, {StringForm["normal at ``", p], ex2 == 0}}, Alignment -> Left, Frame -> All, ItemSize -> 30] }, Frame -> All]]

Note the first 4 lines are relevant. The rest is window dressing for visualization.

Using @cvgmt pts: pts = Cases[ContourPlot[cu == 0, {x, -2, 10}, {y, -2, 10}], GraphicsComplex[pts_, data__] :> pts, -1] // First;

and exporting as animated gif:

enter image description here

Improve this answer
$\endgroup$
4
$\begingroup$

One alternative:

curve = 3 x^2 + 5 y^2 - 7 x y + 2 x - 9 y + 2; {$x, $y} = {8, 7}; slope = D[curve, x]/D[curve, y] /. {x -> $x, y -> $y}; {tangent, orthogonal} = (y - $y) + # (x - $x) slope^# & /@ {1, -1}; ContourPlot[{curve == 0, tangent == 0, orthogonal == 0} , {x,-10,10}, {y, -10, 10} , PlotLegends -> {"Curve", "Tangent", "Orthogonal"} , Epilog -> {Red, PointSize -> Medium, Point[{$x, $y}]} , AspectRatio -> Automatic]

enter image description here

Improve this answer
$\endgroup$
4
$\begingroup$ 
{$tF, $nF} = Table[With[{i = i}, Module[{v = Variables[#]}, Dot[i @ Grad[#, v] /. Thread[v -> #2], v - #2]] &], {i, {Identity, Cross}}];

Examples:

cu = 2 + 2 x + 3 x^2 - 9 y - 7 x y + 5 y^2; pt = {8, 7}; ContourPlot[Evaluate @ {cu == 0, $tF[cu, pt] == 0, $nF[cu, pt]}, {x, -2, 10}, {y, -2, 10}, PlotRange -> {{-2, 10}, {-2, 10}}, Epilog -> {Red , PointSize @ Large, Point @ pt}]

enter image description here

cP[pt_] := ContourPlot[ Evaluate @ {cu == 0, tLF[cu, pt] == 0, nLF[cu, pt]}, {x, -2, 10}, {y, -2, 10}, PlotRange -> {{-2, 10}, {-2, 10}}, Epilog -> {Red , PointSize@Large, Point@pt}]; coords = First @ Cases[ContourPlot[cu == 0, {x, -2, 10}, {y, -2, 10}], GraphicsComplex[c_, ___] :> c, All]; frames = cP /@ coords; Export["tnframes.gif", frames[[;; ;; 2]], DisplayAllSteps -> True]

enter image description here

cu2 = x^4 - 2 x^2 + y^4 - 2 y^2; SeedRandom[1]; pts = RandomSample[{x, y} /. FindInstance[cu2 == 0, {x, y}, Reals, 20], 3]; ContourPlot[Evaluate @ {cu2 == 0, $tL[cu2, pts[[1]]] == 0, $nL[cu2, pts[[1]]] == 0, $tL[cu2, pts[[2]]] == 0, $nL[cu2, pts[[2]]] == 0, $tL[cu2, pts[[3]]] == 0, $nL[cu2, pts[[3]]] == 0}, {x, -2, 2}, {y, -2, 2}, Epilog -> {Red , PointSize@Large, Point /@ pts}]

enter image description here

Improve this answer
$\endgroup$
3
$\begingroup$

A concise form of the tangent line can be obtained with homogeneous coordinates (HC). In HC the ellipse is implicitly written:

m = {{2, 1, -9/2}, {1, 3, -7/2}, {-9/2, -7/2, 5}}; p = {1, x, y}; p.m.p==0 2 + 2 x + 3 x^2 - 9 y - 7 x y + 5 y^2 ==0

This is the same formula as your cu==0

Now the formula for the tangent at {8,7} can be written very simply:

p0={1,8,7}; p0.m.p == 0

enter image description here

As this are homogeneous coordinates, this is the same line as:

-43 + x + 5 y == 0

The normal to a line given by: {a0,a1,a2} through the point {1,b1,b2} on a is:

 {-a1 b2+a2 b1,- a2,a1}

and the equation of this line:

-a1 b2+a2 b1 - a2 x + a1 y ==0

Therefore for your case:

{-1 7 + 5 8, -5, 1} -> {3,-5,1}

resulting in the normal equation:

33 - 5 x + y == 0
Improve this answer
$\endgroup$

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.