5
$\begingroup$

I have tried to create a map using GeoGraphics, and I have not been able to get one with the same quality as the result Wolfram|Alpha gave me.

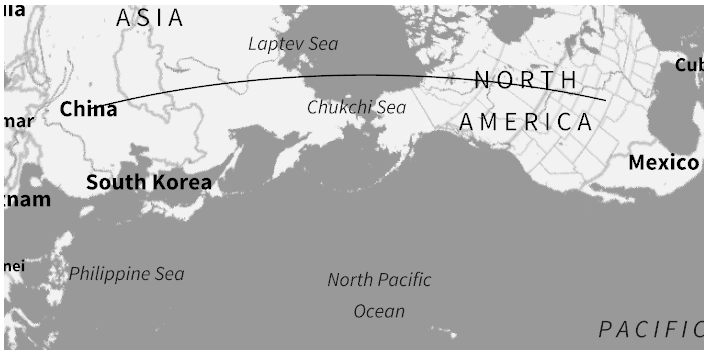
WolframAlpha["distance between eeuu and north korea", {{"Map", 1}, "Content"}]

enter image description here

GeoGraphics[ GeoPath[{Entity["Country", "UnitedStates"], Entity["Country", "China"]}], GeoBackground -> "VectorMonochrome", GeoProjection -> "AzimuthalEquidistant"]

enter image description here

Can I create a similar map with the same quality (the Wolfram|Alpha image is, for example, vectorized) to the one Wolfram|Alpha gave me using GeoGraphics directly?

In fact, this question is related to others that I've seen some people ask on other sites and never got an answer: If I get a result from Wolfram|Alpha, is there any way to, from that result, get the code I can write in Mathematica to generate it? That is, given the image map, how do I get Mathematica to give me the code for that image?

Improve this question
$\endgroup$
2
  • 1
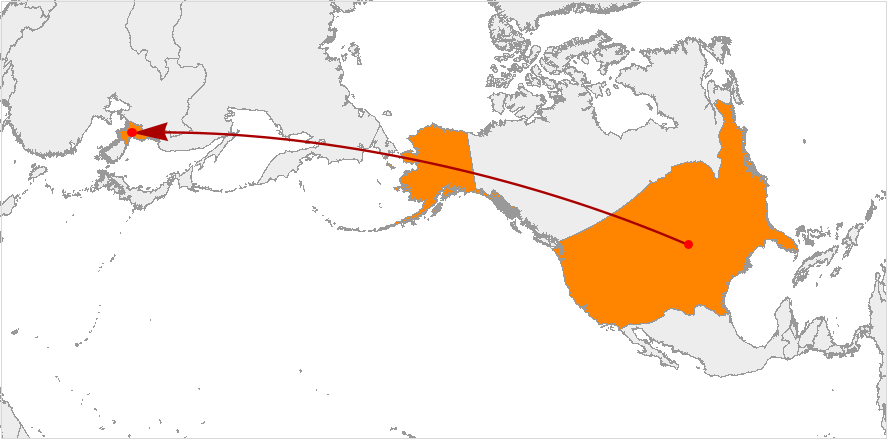
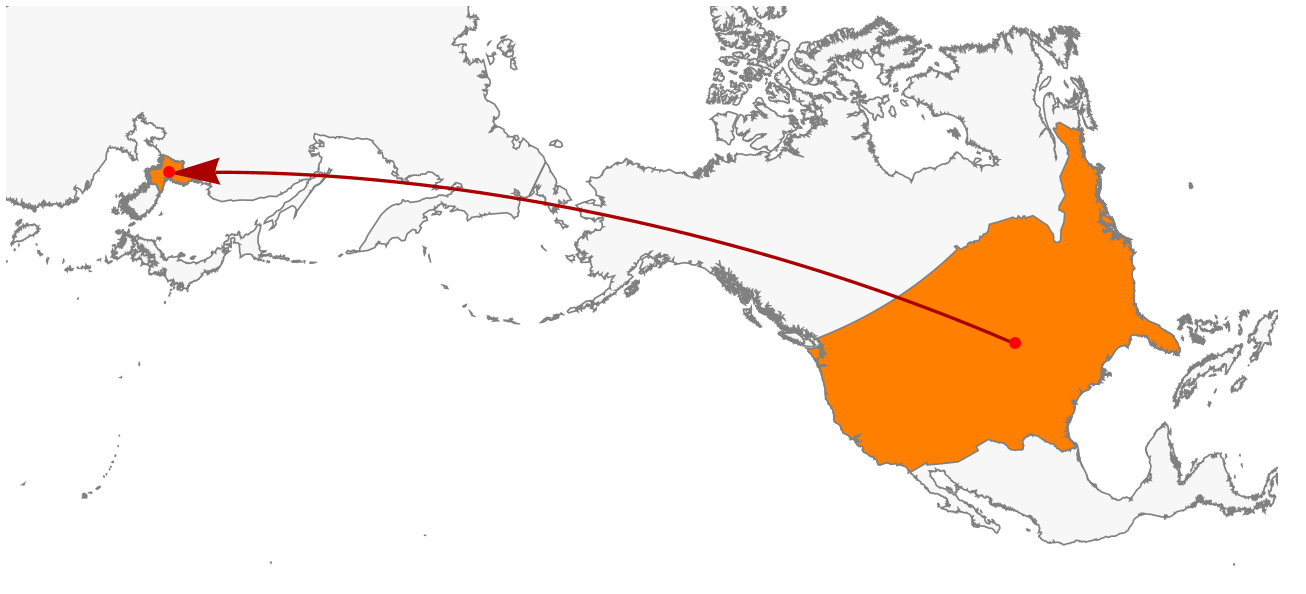
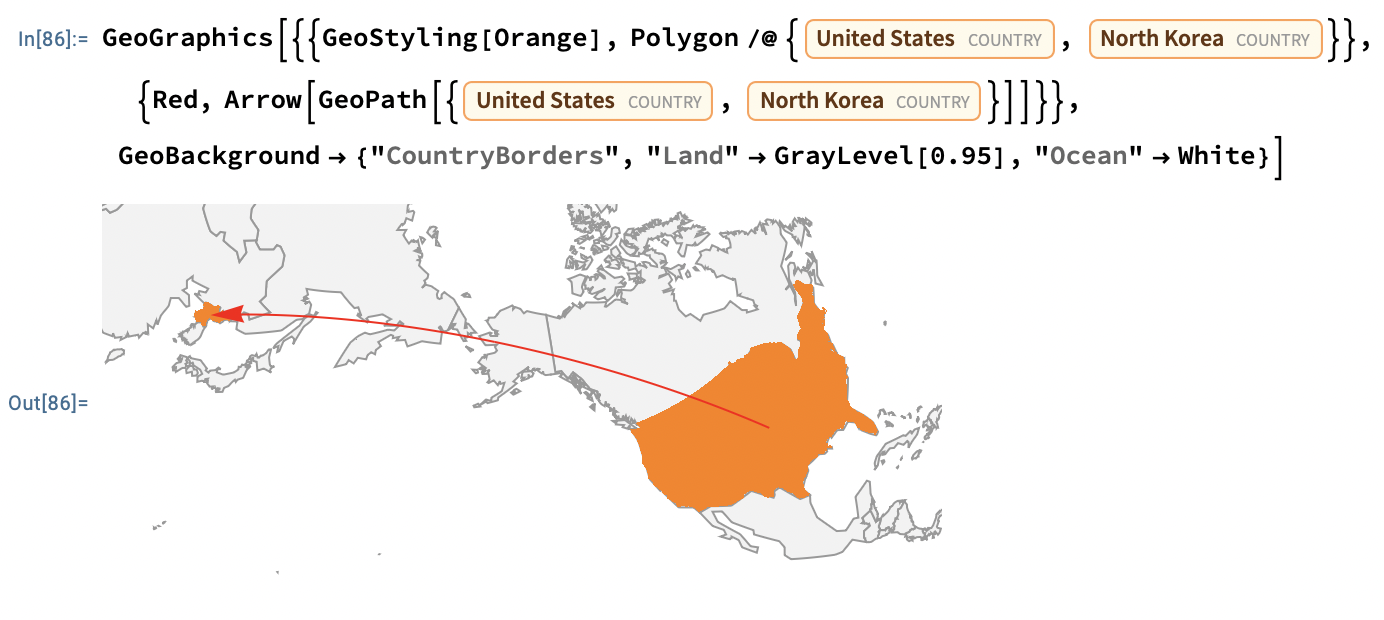
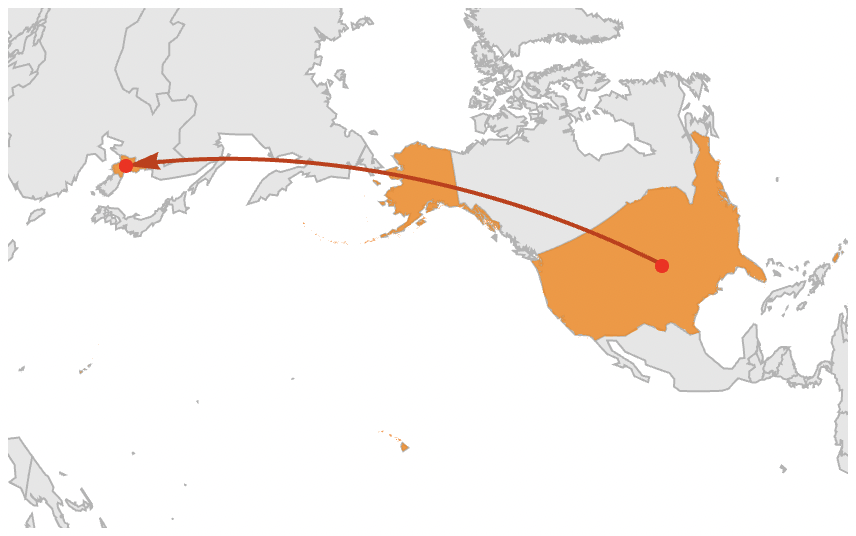
    $\begingroup$ No, I don't think it is possible to get the "raw" code which is used internally in Wolfram|Alpha to generate such plots. However, I don't think it's that difficult to recreate the map. Can you please show us what you've tried so far? For example: even a simple loc1 = Entity["Country", "UnitedStates"];loc2 = Entity["Country", "NorthKorea"]; GeoGraphics[{{FaceForm[Orange], Polygon[loc1], Polygon[loc2]}, Red, Darker@Red, Arrow[GeoPath[{loc1, loc2}]]}, GeoBackground -> "CountryBorders"] comes very close. $\endgroup$ Commented Feb 29, 2024 at 16:51
  • $\begingroup$ Thanks. This is the code I wrote and noticed that the vectorized graphic lost quality when using GeoProjection: GeoGraphics[ GeoPath[{Entity["Country", "UnitedStates"], Entity["Country", "China"]}], GeoBackground -> "VectorMonochrome", GeoProjection -> "AzimuthalEquidistant"] $\endgroup$ Commented Feb 29, 2024 at 16:58

3 Answers 3

Reset to default
7
$\begingroup$

Here is a rough approximation. First, you generate a temporary GeoGraphics just to get correct positioning (GeoCenter, GeoRange ...). Then, you can get a high quality world map from Polygon[Entity["GeographicRegion", "World"]].

loc1 = Entity["Country", "UnitedStates"]; loc2 = Entity["Country", "NorthKorea"]; (* Temporary GeoGraphics *) geo = GeoGraphics[{Polygon[loc1], Polygon[loc2], Arrow[GeoPath[{loc1, loc2}]]}]; GeoGraphics[{{EdgeForm[Gray], FaceForm[LightGray], Polygon[Entity["GeographicRegion", "World"]], GeoStyling[Orange], Polygon[loc1], Polygon[loc2]}, Darker@Red, Thick, Arrow[GeoPath[{loc1, loc2}]], Red, PointSize[Large], Point[{loc1, loc2}]}, GeoBackground -> None, Sequence @@ Options[geo]]

enter image description here

Improve this answer
$\endgroup$
9
$\begingroup$

This is pretty close, I think:

GeoGraphics[{{GeoStyling[Orange], Polygon /@ {Entity["Country", "UnitedStates"], Entity["Country", "NorthKorea"]}}, {Red, Arrow[GeoPath[{Entity["Country", "UnitedStates"], Entity["Country", "NorthKorea"]}]]}}, GeoBackground -> {"CountryBorders", "Land" -> GrayLevel[0.95], "Ocean" -> White}]

enter image description here

Improve this answer
$\endgroup$
1
  • 2
    $\begingroup$ Ah, GeoStyling instead of FaceForm for vivid colors, thanks! $\endgroup$ Commented Feb 29, 2024 at 17:13
7
$\begingroup$

Perhaps something like this:

usa = Entity["Country", "UnitedStates"]; korea = Entity["Country", "NorthKorea"]; GeoGraphics[{ {GeoStyling[Append[Orange, 0.8]], Polygon[GeoVariant[usa, "AllAreas"]], Polygon[korea]}, {ColorData[112, 1], AbsoluteThickness[2], Arrow[GeoPath[{usa, korea}]]}, {Red, PointSize[Large], Point[{usa, korea}]} }, GeoBackground -> {{"CountryBorders", "Land" -> GrayLevel[0.9], "Ocean" -> None, "Border" -> GrayLevel[0.7]}}, GeoProjection -> "LambertAzimuthal", GeoRange -> GeoBounds[GeoGroup[{usa, korea}]], PlotRangePadding -> Scaled[.06], AspectRatio -> 1/GoldenRatio ]
Improve this answer
$\endgroup$

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.