15
$\begingroup$

I wish to produce an image with more than one composite graphics objects which have been modified using Rotate. I feel this should not be difficult, but haven't yet found a solution.

A simple example using only Disk illustrates the problem.

e1 = Rotate[Graphics[Disk[{0, 0}, {1/3, 1/4}]], \[Pi]/3]; e2 = Rotate[Graphics[Disk[{0, 0}, {1/3, 1/4}]], \[Pi]/7];

The following attempt fails:

Show[e1,e2]

Show::gcomb: Could not combine the graphics objects in Show[]

How should this best be achieved ?

Improve this question
$\endgroup$
3
  • 3
    $\begingroup$ I think this is a reasonable question and ought not be closed. $\endgroup$ Commented Aug 20, 2014 at 18:27
  • $\begingroup$ Perhaps you can also make use of this: How to create custom Graphics primitive? $\endgroup$ Commented Aug 20, 2014 at 18:50
  • $\begingroup$ Would'nt be easier to just change the order of Graphics and Rotate? Like this: e1 = Graphics[Rotate[{Blue, Opacity[.75], Disk[{0, 0}, {1/3, 1/4}]}, \[Pi]/3]]; e2 = Graphics[Rotate[{Red, Opacity[.75], Disk[{0, 0}, {1/3, 1/4}]}, \[Pi]/7]]; Show[{e1, e2}] !Mathematica graphics $\endgroup$ Commented Aug 21, 2014 at 2:09

5 Answers 5

Reset to default
17
$\begingroup$

The trick is just to get rid of the internal Graphics heads and then wrap the full expression in Graphics:

{e1, e2} /. Graphics -> Identity // Graphics

enter image description here

Improve this answer
$\endgroup$
6
  • $\begingroup$ A very simple and surprising trick. Of course +1. $\endgroup$ Commented Aug 20, 2014 at 18:42
  • 1
    $\begingroup$ Hopefully master @kguler is proud of his padawan's use of Identity :) $\endgroup$ Commented Aug 20, 2014 at 18:49
  • $\begingroup$ @mfvonh, nice... +1 of course :) $\endgroup$ Commented Aug 20, 2014 at 18:56
  • 6
    $\begingroup$ this works when Graphics has a single argument (e.g. no graphics options in e1 and e2). Otherwise, if, say e2 has the option ImageSize->300, we need something less clean -- like {e1, e2} /. Rotate[Graphics[x_, y_], r_] :> Graphics[Rotate[x, r], y] // Show $\endgroup$ Commented Aug 20, 2014 at 19:03
  • $\begingroup$ @kguler I think that should be y___, otherwise that seems like the best solution yet. $\endgroup$ Commented Aug 21, 2014 at 10:06
9
$\begingroup$

Update

As noted in the comments by @pickett, the function showF in the original post does not preserve the relative positions of the inset graphics. I am not sure if it is possible to fix showF to address this issue. So, instead, I suggest an alternative approach using

show2F := Show[# /. Rotate[Graphics[x_, y___], r__] :> Graphics[Rotate[x, r], y], PlotRange -> All, ImagePadding -> Scaled[.025]] & show2F@{e1, e2, e3}

enter image description here

Original post

An alternative approach similar to @mfvonh's replacement trick: Wrap inner graphics with Inset and the whole thing with Graphics

showF := Graphics[# /. Graphics -> Composition[Inset, Graphics]] &

or using the new Version10 syntax (thanks: @rojo)

Graphics@*ReplaceAll[Graphics->Inset@*Graphics]

Examples:

g1 = Graphics[{Red, Disk[{0, 0}, {1/3, 1/4}]}, ImageSize -> 250]; g2 = Graphics[{Blue, Opacity[.5], Disk[{0, 0}, {1/3, 1/4}]}, ImageSize -> 200]; g3 = Graphics[{Thickness[.03], Line[{{0, -1/2}, {0, 1}}], {Blue, Line[{{0, -1/2}, {1, 1}}]}, First@Plot[x Sin[6 x + 4], {x, -1, 1}, Axes -> False, PlotStyle -> {Thickness[.02], Orange}]}, ImageSize -> 250]; Row[{g1, g2, g3}]

enter image description here

e1 = Rotate[g1, Pi / 3]; e2 = Rotate[g2, Pi / 7]; e3 = Rotate[g3, Pi / 2]; Row[{e1, e2, e3}]

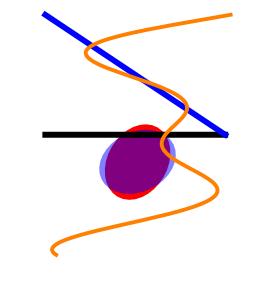
enter image description here

showF @ {e1, e2, e3}

enter image description here

Improve this answer
$\endgroup$
5
  • $\begingroup$ My first upvote "just for laughs" - a brilliant late coup :) $\endgroup$ Commented Aug 20, 2014 at 20:28
  • $\begingroup$ ... and @mfvonh for the key idea. $\endgroup$ Commented Aug 20, 2014 at 20:35
  • $\begingroup$ No cows this time? ;) $\endgroup$ Commented Aug 20, 2014 at 22:11
  • $\begingroup$ @rm-rf, Inset and cows don't mix in v9 -- yet another reason to upgrade to V10 :) $\endgroup$ Commented Aug 20, 2014 at 22:17
  • 1
    $\begingroup$ +1. Similarly, Graphics@*ReplaceAll[Graphics->Inset@*Graphics] $\endgroup$ Commented Aug 21, 2014 at 7:38
7
$\begingroup$

mfvonh's trick is nice, but I think it should be said that the normal approach is to rotate graphics primitives inside the Graphics wrapper.

Graphics[{ Rotate[Disk[{0, 0}, {1/3, 1/4}], π/3], Rotate[Disk[{0, 0}, {1/3, 1/4}], π/7]}, ImageSize -> Small]

graphics

Improve this answer
$\endgroup$
2
  • $\begingroup$ Isn't that what mfvonn does when he changes Graphics to Identity? $\endgroup$ Commented Aug 21, 2014 at 7:41
  • $\begingroup$ @Rojo. Yes, but it's rather the long way around the barn (as we say in the US), don't you think. This post is to make sure beginners see the way it normally done when they read this questions and its answers. $\endgroup$ Commented Aug 21, 2014 at 12:15
6
$\begingroup$

As with some of the other approaches, the following does not maintain relative positions.

e1 = Rotate[Graphics[{Blue, Opacity[.75], Disk[{0, 0}, {1/3, 1/4}]}], \[Pi]/3]; e2 = Rotate[Graphics[{Red, Opacity[.75], Disk[{0, 0}, {1/3, 1/4}]}], \[Pi]/7]; Show[ Rasterize[#, Background -> None] & /@ {e1, e2}]

enter image description here

Improve this answer
$\endgroup$
3
$\begingroup$

Yet another method is to use Overlay. Borrowing Bob Hanlon's example:

e1 = Rotate[Graphics[{Blue, Opacity[.75], Disk[{0, 0}, {1/3, 1/4}]}], π/3]; e2 = Rotate[Graphics[{Red, Opacity[.75], Disk[{0, 0}, {1/3, 1/4}]}], π/7]; Overlay[{e1, e2}]

enter image description here

Improve this answer
$\endgroup$
2
  • 2
    $\begingroup$ With the caveat, as was noted in the comments to my deleted answer that at once point included Overlay, that the objects lose their relative positions. $\endgroup$ Commented Aug 21, 2014 at 9:22
  • $\begingroup$ @Pickett True, but kguler's Inset solution has the same problem as currently written. I still think this is useful. $\endgroup$ Commented Aug 21, 2014 at 10:05

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.