I want to export an animation(gif type) for polar plot $r=\cos 2\theta$ like to the following gif. how can I do it?
$\begingroup$ $\endgroup$
Add a comment |
3 Answers
$\begingroup$ $\endgroup$
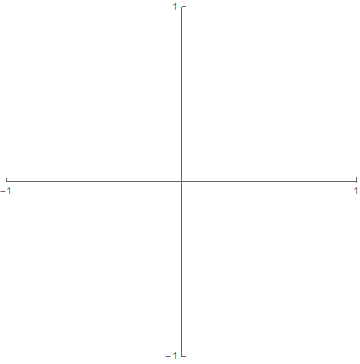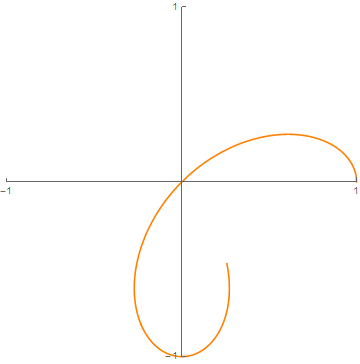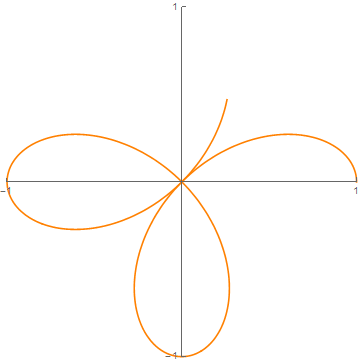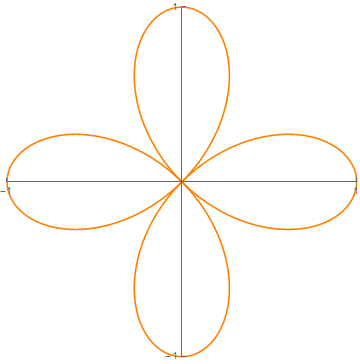
rose = Table[PolarPlot[Cos[x i], {i, 0, Pi}, PlotRange -> 1], {x, 0, 10, .1}];
Followed by:
Export["rose.gif", rose]
Which gives you the following beautiful animation:
You can change the final number of petals by changing the number 10. You can change the speed of the animation by making the increments smaller than .1.
$\begingroup$ $\endgroup$
2 To realize the constant-speed drawing, you'll need to re-parameterize the equation to use the arc-length parameter:
$$ \mathrm{d}s = \left\| \frac{\mathrm{d}\,\boldsymbol{\mathrm{r}}(\theta)}{\mathrm{d}\theta}\right\|\mathrm{d}\theta $$
r = Cos[2 θ] {Cos[θ], Sin[θ]} reParaEq = θ'[s] == 1/FullSimplify[Sqrt[#.#] &@D[r, θ] /. θ -> θ[s]] θFunc = DSolveValue[{reParaEq, θ[0] == 0}, θ, s][s] (* And the max value of the arc-length: *) {sMax} = s /. Solve[θFunc == 2 π, s] To actually plotting the expected result, we need to turn off MaxRecursion:
wholePlot = ParametricPlot[Evaluate[r /. θ -> θFunc], {s, 0, sMax}, PlotPoints -> 200, MaxRecursion -> 0 ] frames = wholePlot /. ({Line[pts_] :> Line[pts[[;; #]]]} & /@ Range[200]); To show the animation in Mathematica, we can use ListAnimate:
ListAnimate[frames, 60] To export it as GIF:
Export["FourLeaveRose.gif", frames, "GIF", "DisplayDurations" -> 1/60, AnimationRepetitions -> ∞]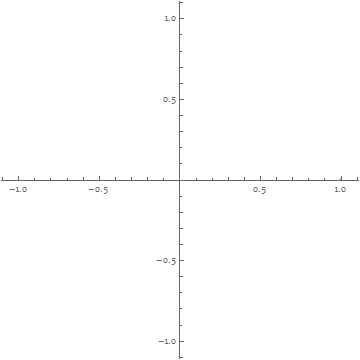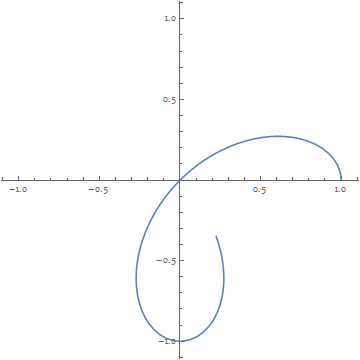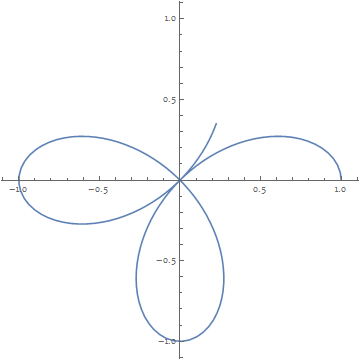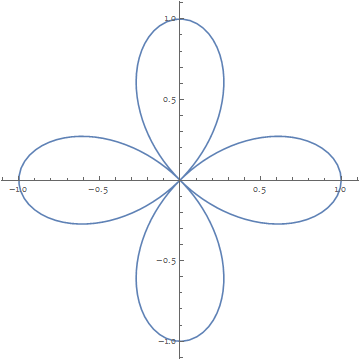 
- $\begingroup$ To @Silvia Why is your code hard and exotic?!!! Please look at my code in my answer. $\endgroup$Nimbigli– Nimbigli2014-12-01 14:34:03 +00:00Commented Dec 1, 2014 at 14:34
- $\begingroup$ @bigli It's not exotic at all... just normal differential geometry -- Basically, the so-called natural parameterization walks along the curve with speed proportionally to arc-length $s$, so will force
Plotusing equally distributed sampled points. (But yes, this effect may not be what you required.) The second benefit of my method would be only invokingPlotonce, which is more efficient. Also, I would like to point out the"DisplayDurations"option of GIF export, in case it might be handy for you. $\endgroup$Silvia– Silvia2014-12-01 15:26:17 +00:00Commented Dec 1, 2014 at 15:26
$\begingroup$ $\endgroup$
2 BE HAPPY!! The easiest code is:
a:= Show[PolarPlot[Cos[2 \[Theta]], {\[Theta], 0, t}], PlotRange -> {{-1, 1}, {-1, 1}}] b= ParallelTable[a, {t, 0.001, 2 Pi, (2 Pi - 0.001)/100}]; Export["4-leaved-rose.gif",b ] and the result is:
- $\begingroup$ Look at both of them. you should find out difference of them. My answer is just answer of the principal question. $\endgroup$Nimbigli– Nimbigli2014-12-01 14:41:18 +00:00Commented Dec 1, 2014 at 14:41
- 1$\begingroup$ You should read Aron's answer more carefully, he shows you how you can write a better code which is even simpler. Another simple one-liner:
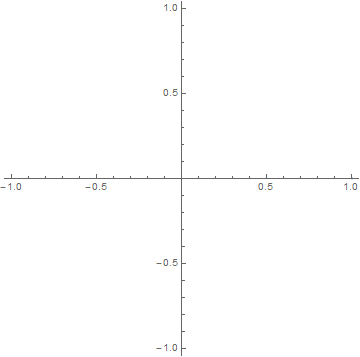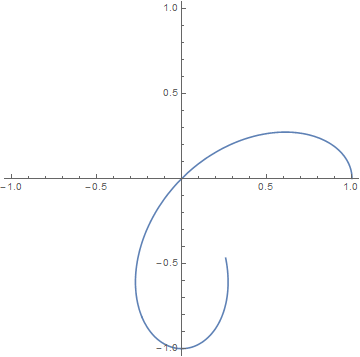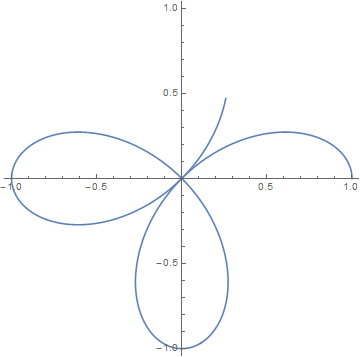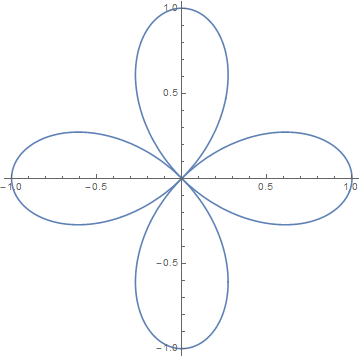
b = PolarPlot[Cos[2 [Theta]], {\[Theta], $MachineEpsilon, #}, PlotRange -> 1] & /@ Range[0, 2 Pi, 0.02 Pi];$\endgroup$2014-12-02 02:39:52 +00:00Commented Dec 2, 2014 at 2:39