41
$\begingroup$

Does anyone know if there are any plans to develop an MCMC capability in Mathematica?

My reasoning for asking is that as it stands, I can't seem to find any 'out-of-the-box' functions/capabilities for doing computational Bayesian statistics. For the simple case, coding an MCMC algorithm is easy, but for hierarchical models, this is more complex, and others have implemented various efficient algorithms in BUGS, STAN or JAGS.

It seems like it would be a good addition to future versions of the software, and was just wondering whether anyone knew whether this is being considered.

Improve this question
$\endgroup$
2
  • 10
    $\begingroup$ I don't know whether WRI has any plans for developing MCMC. However, Phil Gregory has developed a MCMC package in Mathematica. You can download it at bit.ly/1tdaYhG under "Resources". BTW, I can recommend his book "Bayesian Logical Data Analysis for the Physical Sciences" in which he explains MCMC at length. $\endgroup$ Commented Feb 14, 2015 at 11:39
  • 2
    $\begingroup$ There is some hidden MCMC code in Mathematica you can use. See mathematica.stackexchange.com/a/212930/43522 $\endgroup$ Commented Oct 6, 2020 at 10:24

3 Answers 3

Reset to default
31
$\begingroup$

Update: 2/7/2019 I have just released a new version of the package: MathematicaStan v2.0

I just have released a beta version of MathematicaStan, a package to interact with CmdStan.

https://github.com/vincent-picaud/MathematicaStan

Usage example:

(* Defines the working directory and loads CmdStan.m *) SetDirectory["~/GitHub/MathematicaStan/Examples/Bernoulli"] Needs["CmdStan`"] (* Generates the Bernoulli Stan code and compiles it *) stanCode="data { int<lower=0> N; int<lower=0,upper=1> y[N]; } parameters { real<lower=0,upper=1> theta; } model { theta ~ beta(1,1); for (n in 1:N) y[n] ~ bernoulli(theta); }"; Export["bernoulli.stan",stanCode,"Text"] (* Compile your code. * Caveat: this can take some time *) StanCompile["bernoulli"]

--- Translating Stan model to C++ code --- bin/stanc \ /home/pix/GitHub/MathematicaStan/Examples/Bernoulli/bernoulli.stan \ --o=/home/pix/GitHub/MathematicaStan/Examples/Bernoulli/bernoulli.hpp Model name=bernoulli_model Input file=/home/pix/GitHub/MathematicaStan/Examples/Bernoulli/\ bernoulli.stan Output file=/home/pix/GitHub/MathematicaStan/Examples/Bernoulli/\ bernoulli.hpp

--- Linking C++ model --- g++ -I src -I stan/src -isystem stan/lib/stan_math/ -isystem \ stan/lib/stan_math/lib/eigen_3.2.8 -isystem \ stan/lib/stan_math/lib/boost_1.60.0 -isystem \ stan/lib/stan_math/lib/cvodes_2.8.2/include -Wall -DEIGEN_NO_DEBUG \ -DBOOST_RESULT_OF_USE_TR1 -DBOOST_NO_DECLTYPE -DBOOST_DISABLE_ASSERTS \ -DFUSION_MAX_VECTOR_SIZE=12 -DNO_FPRINTF_OUTPUT -pipe -lpthread \ -O3 -o /home/pix/GitHub/MathematicaStan/Examples/Bernoulli/bernoulli \ src/cmdstan/main.cpp -include \ /home/pix/GitHub/MathematicaStan/Examples/Bernoulli/bernoulli.hpp \ stan/lib/stan_math/lib/cvodes_2.8.2/lib/libsundials_nvecserial.a \ stan/lib/stan_math/lib/cvodes_2.8.2/lib/libsundials_cvodes.a

(* Generates some data and saves them (RDump file) *) n=1000; y=Table[Random[BernoulliDistribution[0.2016]],{i,1,n}]; RDumpExport["bernoulli",{{"N",n},{"y",y}}]; (* Runs Stan and gets result *) StanRunSample["bernoulli"] output=StanImport["output.csv"];

(Not shown because too long, CmdStan output: MCMC sampling)

(* You can access to output: variable names, data matrix... *) StanImportHeader[output] Dimensions[StanImportData[output]] Take[StanImportData[output],3]

{{"lp__", 1}, {"accept_stat__", 2}, {"stepsize__", 3}, {"treedepth__", 4}, {"n_leapfrog__", 5}, {"divergent__", 6}, {"energy__", 7}, {"theta", 8}}

{1000, 8}

{{-532.463, 0.693148, 1.47886, 1., 1., 0., 533.321, 0.226882}, {-532.563, 0.974395, 1.47886, 1., 1., 0., 532.581, 0.230357}, {-532.629, 0.982728, 1.47886, 1., 1., 0., 532.7, 0.231909}}

(* Plots theta 1000 sample and associated histogram *) ListLinePlot[Flatten[StanVariableColumn["theta", output]],PlotLabel->"\[Theta]"] Histogram[Flatten[StanVariableColumn["theta", output]],PlotLabel->"\[Theta]"]

enter image description here

enter image description here

Feedback are welcome, especially for Windows as I only use Linux.

Improve this answer
$\endgroup$
2
  • 3
    $\begingroup$ Could you give a small usage example within your answer? It's not mandatory, but it would immediately give a clearer picture of what the package can do. $\endgroup$ Commented Sep 16, 2016 at 10:03
  • $\begingroup$ Sure, I tried to cut/copy one example and hope the result is not too ugly. $\endgroup$ Commented Sep 16, 2016 at 13:29
28
$\begingroup$

For the sake of completeness let me advertise someone else's code which implements MCMC in mathematica.

Josh Burkart has implemented Mathematica Markov Chain Monte Carlo which is available on github.

His read-me reads:

Mathematica Markov Chain Monte Carlo

Mathematica package containing a general-purpose Markov chain Monte Carlo routine Josh Burkart wrote. Includes various examples and documentation.

Features:

  • Convenience wrapper for fitting models to arbitrary-dimensional data with Gaussian errors
  • Handles both real-valued and discrete-valued model parameters
  • Uses Metropolis algorithm with decaying exponential proposal distribution
  • Progress monitor; support for auto save/resume

Files:

  • mcmc.m: Package file
  • mcmc_demonst.nb: Demonstrations and documentation

For a good Python MCMC implementation, check out emcee.

?MCMC

 MCMC[plogexpr, paramspec, numsteps]

Perform MCMC sampling of the supplied probability distribution.

  1. plogexpr should be an expression that gives the unnormalized log probability for a particular choice of parameter values.

  2. paramspec either gives the results of a previous MCMC run (w/ same plogexpr--just to add on more iterations), or lists the model \ parameters like so: {{param1, ival1, spread1, domain1}, ...} a) Each param should be symbolic. b) ival is the initial parameter value. c) spread is roughly how far to try to change the parameter each step \ in the Markov chain. In this routine we select new parameters values based on an exponential distribution of the form \ Exp[[CapitalDelta]param/spread]. My Numerical Recipes book advises setting these spreads so that the \ average candidate acceptance is 10-40%. d) Each domain is either Reals or a list of all possible values the parameter can take on (needs to be a uniform grid).

  3. numsteps is the number of Markov chain steps to perform.

In his demonstration, the simplest example reads

{μ1, μ2} = {1, -2}; {σ1, σ2} = {1.2, 3.4}; plogexpr = Log[PDF[NormalDistribution[μ1, σ1], x1] PDF[NormalDistribution[μ2, σ2], x2]]; mcmc = MCMC[plogexpr, {{x1, 0, 2, Reals}, {x2, 0, 2, Reals}}, 100000]

Mathematica graphics

The result provides

mcmc["Properties"]

{"BestFitParameters", "ParameterErrors", "AverageAcceptance", "TimeSpent", "NumSteps", "Parameters", "ProposalSpreads", "ParameterDomains", "BurnFraction", "BurnEnd", "CorrelationMatrix", "ParameterRun", "ParametersLogPRun", "TransitionLogPRun", "ParameterRunPlots", "ParameterHistograms"}

For instance,

mcmc["ParameterHistograms"]

Mathematica graphics

mcmc["ParameterRun"] // SmoothDensityHistogram[#, "Oversmooth", "PDF", ColorFunction -> ColorData["Rainbow"], Mesh -> 3, MeshStyle -> Directive[White, Dashed]] &

Mathematica graphics

The package provides MCMCModelFit.

MCMCModelFit[data, errors, model, paramspec, ivars, numsteps] Perform MCMC samping of the probability distribution resulting from modeling data with model, assuming Gaussian errors.

For instance 

error = 1.5; dattab = Table[{x, 1.3 x - 2 Sin[2 x] + 7 + RandomVariate[NormalDistribution[0, error]]}, {x, 0, 10, .1}]; errors = Table[error, {x, 0, 10, .1}]; spr = .04; mcmc = MCMCModelFit[dattab, errors, a x + b Sin[c x] + d, {{a, 1.3, spr, Real}, {b, -2, spr, Real}, {c, 2, spr, Real}, {d, 7, spr, Real}}, {x}, 100000];

produces

 Show[ListPlot[dattab, Joined -> False], Plot[{7 + 1.3 x - 2 Sin[2 x], a x + b Sin[c x] + d /. mcmc["BestFitParameters"]}, {x, 0, 10}, PlotStyle -> {Directive[Red, Dashed, Opacity[1]], Blue}]]

Mathematica graphics

More generally, the author of this package gives a sequence of examples of increasing complexity  in his demonstration notebook. 

It involves things like radial velocity  curves such as this:

Mathematica graphics

Needless to say all the credit is his.

Complementary worked example

As a complement, let us consider the problem of estimating the parameters of a MultinormalDistribution from a dataset drawn from it.

dat = RandomVariate[ MultinormalDistribution[{1, 0.5}, {{1, 0.95}, {0.95, 1}}], 100]; dat // Histogram3D

Mathematica graphics

Let us define the corresponding proposition PDF

Clear[logpdf]; logpdf[a_, b_, c_] := LogLikelihood[MultinormalDistribution[{a, b}, {{1, c}, {c, 1}}], dat];

and apply MCMC to estimate the corresponding most likely parameters

mcmc = MCMC[logpdf[a, b, c], { {a, 0.9, 0.3, Reals}, {b, 0.4, 0.2, Reals}, {c, 0.9, 0.2, Reals} }, 150000]; mcmc[{"BestFitParameters", "ParameterErrors", "ProposalSpreads", "ParameterHistograms"}]

Mathematica graphics

As expected the first two parameters are strongly correlated:

 mcmc["CorrelationMatrix"]

Mathematica graphics

which we can check by looking at the histogram of sampled points:

Most /@ mcmc["ParameterRun"] // SmoothDensityHistogram[#, "Oversmooth", "PDF", ColorFunction -> ColorData["Rainbow"], Mesh -> 5, MeshStyle -> Directive[White, Dashed]] &,

Mathematica graphics

Finally see this question on how to use it in parallel.

Improve this answer
$\endgroup$
10
  • $\begingroup$ Have you used this yourself? If yes, what do you think? When you come across a good package, please do add it to packagedata.net You can log in with your SE account and your reputation gives you full access (no need to wait for moderation). $\endgroup$ Commented Feb 12, 2017 at 17:02
  • 1
    $\begingroup$ It seems to be pure Mathematica. I wonder how that affects performance. I think LibraryLink, and in particular the features made easy to use by LTemplate, would be an excellent candidate for a high performance implementation. $\endgroup$ Commented Feb 12, 2017 at 17:04
  • $\begingroup$ The Metropolis algorithm does not parallelize trivially (although multiple parallel runs are often useful for sampling). What I meant was a full rewrite in C++. The algorithm itself is easy and quick to implement. After a quick look, I like the package design, it's made to be consistent and easy to use. $\endgroup$ Commented Feb 12, 2017 at 17:20
  • $\begingroup$ @Szabolcs would you happen to have a simple implementation of the Metropolis algorithm? I would like to run different draws in // and the above code is not parallel friendly (calls to Monitor etc..)? cf my question here mathematica.stackexchange.com/q/139133/1089 $\endgroup$ Commented Mar 3, 2017 at 14:19
  • 1
    $\begingroup$ Here's a quick and dirty Metropolis sampler. $\endgroup$ Commented Mar 3, 2017 at 14:43
15
$\begingroup$

This answer gives explicitly a (parallel) MCMC implementation in mathematica following closely this Wolfram Demonstrations Project. This basically involves only a few lines: 

mcmcfunComp = Compile[{{s, _Real, 1}}, Module[{xm, ym, proposal, xp, yp, p2, p1, proposalSigma = 0.2}, {xm, ym} = s; xp = RandomReal[NormalDistribution[xm, proposalSigma]]; yp = RandomReal[NormalDistribution[ym, proposalSigma]]; p2 = pdf[xp, yp]; p1 = pdf[xm, ym]; proposal = p2/p1; If[RandomReal[] <= proposal, {xp, yp}, {xm, ym}]], (* THIS IS THE MCMC STEP *) CompilationOptions -> {"InlineExternalDefinitions" -> True}, Parallelization -> True, CompilationTarget -> "C"]; sim = NestList[mcmcfunComp[#] &, {-4, 9}, 1000000];

and is quite fast!

Illustration

As an illustration (so as to actually contribute something other than a link) let us implement it on a 4D PDF

Let us first define the 4D PDF as a simple sum of Gaussians

Clear[pdf0, pdf1, pdf2, pdf, pdfN]; pdf0 = MultinormalDistribution[{1, 0, -1, 1}, 1/8 {{1, 0, 0, 0}, {0, 1, 0, 0}, {0, 0, 1, 0}, {0, 0, 0, 1}}]; pdf1 = MultinormalDistribution[{1, 1, 0, 1}, 1/8 {{1, 0, 0, 0}, {0, 1, 0, 0}, {0, 0, 1, 0}, {0, 0, 0, 1}}]; pdf2 = MultinormalDistribution[{0, -1, 1, 0}, 1/8 {{1, 0, 0, 0}, {0, 1, 0, 0}, {0, 0, 1, 0}, {0, 0, 0, 1}}]; pdf[x_, y_, z_, t_] = PDF[pdf0, {x, y, z, t}] + 1/2. PDF[pdf1, {x, y, z, t}] + 1/4. PDF[pdf2, {x, y, z, t}];

Then Compile the function

pdfN = Compile[{{x, _Real}, {y, _Real}, {z, _Real}, {t, _Real}}, pdf[x, y, z, t] // Evaluate, Parallelization -> True, CompilationTarget -> "C"];

Now the mcmc function itself obeys

mcmcfun = Compile[{{s, _Real, 1}}, Module[{xm, ym, zm, tm, proposal, xp, yp, zp, tp, p2, p1, proposalSigma = 1}, {xm, ym, zm, tm} = s; xp = RandomReal[NormalDistribution[xm, proposalSigma]]; yp = RandomReal[NormalDistribution[ym, proposalSigma]]; zp = RandomReal[NormalDistribution[zm, proposalSigma]]; tp = RandomReal[NormalDistribution[tm, proposalSigma]]; p2 = pdfN[xp, yp, zp, tp]; p1 = pdfN[xm, ym, zm, tm]; proposal = p2/p1; If[RandomReal[] <= proposal, {xp, yp, zp, tp}, {xm, ym, zm, tm}]], CompilationOptions -> {"InlineExternalDefinitions" -> True}, Parallelization -> True, CompilationTarget -> "C"];

and is indeed fast and straightforward to iterate.

sim = Drop[NestList[mcmcfun[#] &, {0, 0, 0, 0}, 1000000], {1, 1000}];

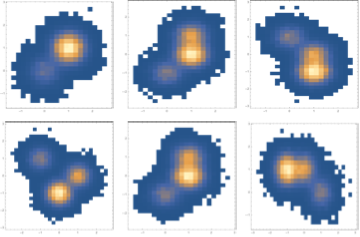
We can see by looking at different projections that it has indeed sampled the PDF

{{{First[#], Last[#]} & /@ sim // DensityHistogram // Image, {First[#], #[[2]]} & /@ sim // DensityHistogram // Image, {First[#], #[[3]]} & /@ sim // DensityHistogram // Image}, {{#[[2]], #[[3]]} & /@ sim // DensityHistogram // Image, {#[[4]], #[[2]]} & /@ sim // DensityHistogram // Image, {#[[3]], #[[4]]} & /@ sim // DensityHistogram // Image}} // GraphicsGrid

Mathematica graphics

Improve this answer
$\endgroup$

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.