{$tF, $nF} = Table[With[{i = i}, Module[{v = Variables[#]}, Dot[i @ Grad[#, v] /. Thread[v -> #2], v - #2]] &], {i, {Identity, Cross}}]; Examples:
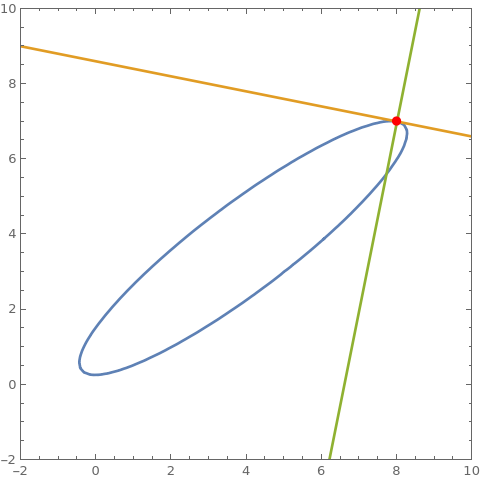
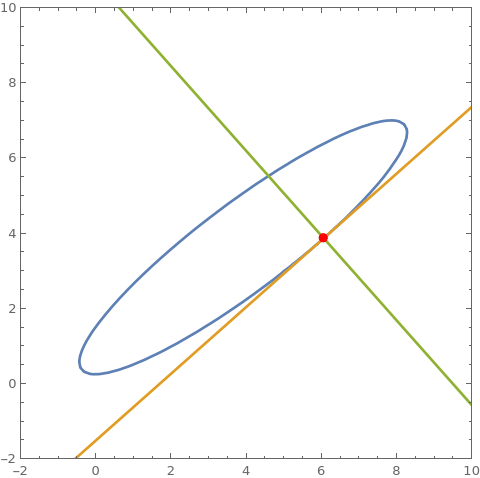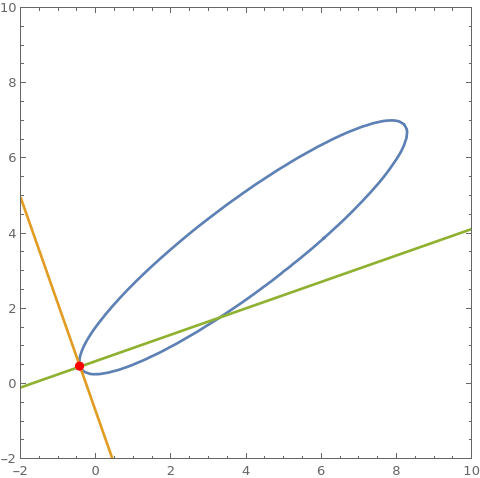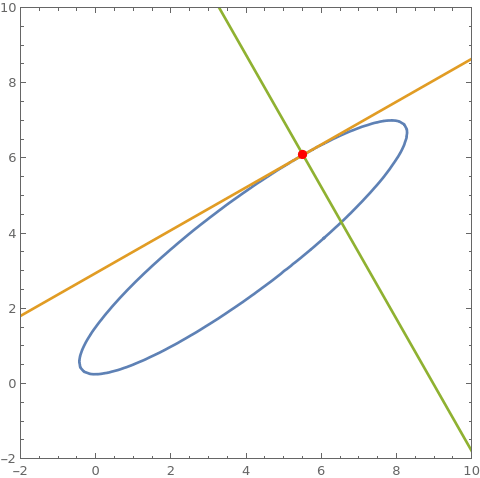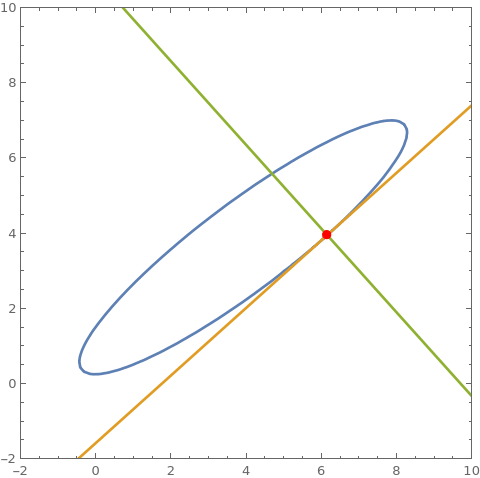
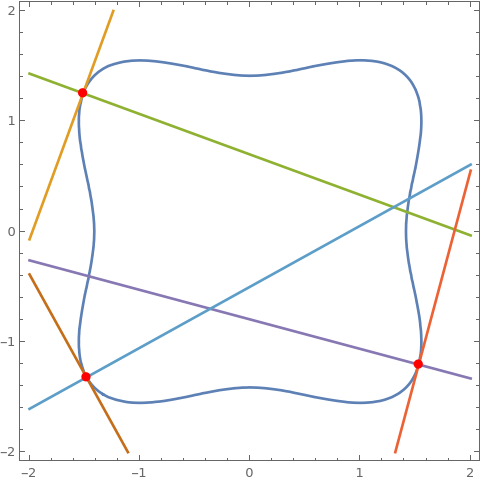
cu = 2 + 2 x + 3 x^2 - 9 y - 7 x y + 5 y^2; pt = {8, 7}; ContourPlot[Evaluate @ {cu == 0, $tF[cu, pt] == 0, $nF[cu, pt]}, {x, -2, 10}, {y, -2, 10}, PlotRange -> {{-2, 10}, {-2, 10}}, Epilog -> {Red , PointSize @ Large, Point @ pt}] cP[pt_] := ContourPlot[ Evaluate @ {cu == 0, tLF[cu, pt] == 0, nLF[cu, pt]}, {x, -2, 10}, {y, -2, 10}, PlotRange -> {{-2, 10}, {-2, 10}}, Epilog -> {Red , PointSize@Large, Point@pt}]; coords = First @ Cases[ContourPlot[cu == 0, {x, -2, 10}, {y, -2, 10}], GraphicsComplex[c_, ___] :> c, All]; frames = cP /@ coords; Export["tnframes.gif", frames[[;; ;; 2]], DisplayAllSteps -> True] cu2 = x^4 - 2 x^2 + y^4 - 2 y^2; SeedRandom[1]; pts = RandomSample[{x, y} /. FindInstance[cu2 == 0, {x, y}, Reals, 20], 3]; ContourPlot[Evaluate @ {cu2 == 0, $tL[cu2, pts[[1]]] == 0, $nL[cu2, pts[[1]]] == 0, $tL[cu2, pts[[2]]] == 0, $nL[cu2, pts[[2]]] == 0, $tL[cu2, pts[[3]]] == 0, $nL[cu2, pts[[3]]] == 0}, {x, -2, 2}, {y, -2, 2}, Epilog -> {Red , PointSize@Large, Point /@ pts}]