Return to Revisions

Edit

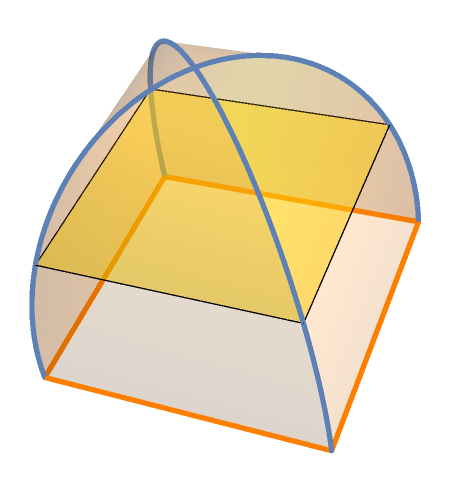
• The length of the square is Sqrt[3^2 - x^2] means that it's 4 points are squares[x] as below.(the height x is the parameter).

• For every 0<=x<=3, we join the 4 points squares[x] to build the surface.

Clear["Global`*"]; squares[x_] := {{-(Sqrt[3^2 - x^2]/2), -(Sqrt[3^2 - x^2]/2), x}, {Sqrt[3^2 - x^2]/2, -(Sqrt[3^2 - x^2]/2), x}, {(Sqrt[3^2 - x^2]/2), Sqrt[3^2 - x^2]/2, x}, {-Sqrt[3^2 - x^2]/2, Sqrt[3^2 - x^2]/2, x}}; lines = ParametricPlot3D[squares[x], {x, 0, 3}, BoxRatios -> Automatic]; surface = ParametricPlot3D[{1 - s, s} . # & /@ Partition[squares[x], 2, 1, 1], {x, 0, 3}, {s, 0, 1}, Boxed -> False, Mesh -> None, PlotStyle -> Opacity[.2], Axes -> False, PlotPoints -> 60, MaxRecursion -> 0]; Show[lines, surface, Graphics3D[{FaceForm[Directive@{Opacity[.5], Yellow}], Polygon[squares[1.5]], FaceForm[], EdgeForm[Directive@{Orange, Thick}], Polygon[squares[0]]}], Boxed -> False, Axes -> False] 

• To calculate the volume,one way is using Integrate to accumulate the square area which length is Sqrt[3^2 - x^2].

Integrate[(Sqrt[3^2 - x^2])^2, {x, 0, 3}] 

18 or build the BoundaryMeshRegion

Clear[ptss, bm]; squares[x_] := {{-(Sqrt[3^2 - x^2]/2), -(Sqrt[3^2 - x^2]/2), x}, {Sqrt[3^2 - x^2]/2, -(Sqrt[3^2 - x^2]/2), x}, {(Sqrt[3^2 - x^2]/2), Sqrt[3^2 - x^2]/2, x}, {-Sqrt[3^2 - x^2]/2, Sqrt[3^2 - x^2]/2, x}}; ptss = Table[squares[x], {x, Most@Subdivide[0, 3, 10^3]}]; {m, n, p} = Dimensions[ptss]; bm = BoundaryMeshRegion[ Catenate[ ptss], {Table[ Polygon[{{#1[[1]], #2[[1]], #2[[2]]}, {#1[[2]], #1[[1]], \ #2[[2]]}}] & @@@ Thread@{Partition[Range[1, n] + j*n, 2, 1, 1], Partition[Range[1, n] + (j + 1)*n, 2, 1, 1]}, {j, 0, m - 2}], Polygon[Range[1, n]], Polygon[Range[1, n] + (m - 1)*n]}] bm // Volume 

18.

Original

• A staring point.
• We draw the intersection line of two cylinders.

ContourPlot3D[{x^2 + z^2 == 3^2, y^2 + z^2 == 3^2}, {x, -3, 3}, {y, -3, 3}, {z, -3, 3}] 

Clear["Global`*"]; plot = Plot3D[z = Sqrt[3^2 - y^2], {x, -3, 3}, {y, -3, 3}, Mesh -> {{0}}, MeshFunctions -> Function[{x, y, z}, z - Sqrt[3^2 - x^2]], MeshStyle -> Directive@{Thick, Red}, PlotPoints -> 150, MaxRecursion -> 4, PlotStyle -> None, BoundaryStyle -> None, Boxed -> False, Axes -> False, BoxRatios -> Automatic]; square[x_] := Graphics3D[{FaceForm[], EdgeForm[Blue], GeometricTransformation[ Polygon[{{-1, -1, 0}, {1, -1, 0}, {1, 1, 0}, {-1, 1, 0}}], TranslationTransform[{0, 0, x}]@* ScalingTransform[Sqrt[3^2 - x^2]*{1, 1, 1}]]}]; n=2; Show[plot, Table[square[x], {x, Subdivide[0, 3, n]}], BoxRatios -> Automatic] 

n=25; Show[plot, Table[square[x], {x, Subdivide[0, 3, n]}], BoxRatios -> Automatic, ViewPoint -> {1, 1, 2}]