I would like to understand, how to obtain gradients of the PDE solution obtained with NDSolve. To be precise let us consider a Laplace equation from one of the examples:

 Clear[x, y, f]; emesh = ToElementMesh[Disk[]]; f = NDSolveValue[{\!\( \*SubsuperscriptBox[\(\[Del]\), \({x, y}\), \(2\)]\(u[x, y]\)\) == 0, DirichletCondition[u[x, y] == Sin[x y], True]}, u, {x, y} \[Element] emesh] 

This returns the interpolation function which one can plot and integrate:

 NIntegrate[f[x, y], {x, y} \[Element] emesh] (* 1.52794*10^-8 *) Plot3D[f[x, y], {x, y} \[Element] emesh]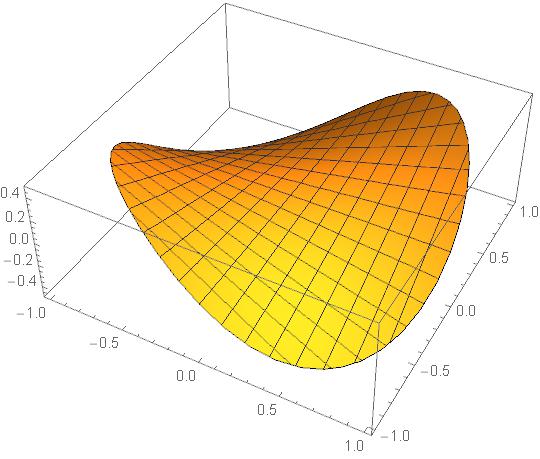 

This, however, does not work:

 g[x_, y_] := D[f[x, y], x]; Plot3D[g[x, y], {x, y} \[Element] emesh] 

Since Integrate does not work on this result, only NIntegrate does, the problem is probably that one needs to apply a numeric derivative. What and how?