Two Diehards Make a Glider
game-of-life code-challenge source-layout
In Conway's Game of Life, there is an infinite square grid of cells, each of which is alive or dead. The pattern changes each "generation". A dead cell with exactly 3 live neighbors (orthogonal or diagonal) becomes a live cell. A live cell only lives to the next generation if it has 2 or 3 live neighbors. These simple rules lead to very complex behaviors. The most well-known pattern is the glider, a pattern that moves diagonally one cell every 4 generations and looks like this:
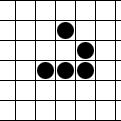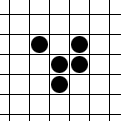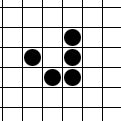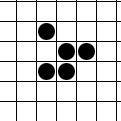
The Challenge
Your task is to create two patterns which will eventually result in an empty board when by themselves (a.k.a. a diehard), but when combined in a certain non-bordering and non-overlapping arrangement, eventually spawn a single glider and nothing else.POSTED
Rules and Scoring
- Each of the lone diehards must fit all live cells within a 100x100 cell box and may not contain more than 100 live cells.
- The combination glider synthesizer must contain both diehards such that their bounding boxes surrounding all live cells are separated by at least one dead cell.
- It does not matter which direction the single glider is facing
- Your score is the sum of the number of generations it takes to get to the goal state for each of the 3 initial patterns. Highest score wins.
