NDSolve Method Plugin Framework
Introduction
The control mechanisms set up for
NDSolve enable you to define your own numerical integration algorithms and use them as specifications for the
Method option of
NDSolve.
NDSolve accesses its numerical algorithms and the information it needs from them in an object-oriented manner. At each step of a numerical integration,
NDSolve keeps the method in a form so that it can keep private data as needed.
The structure for method data used in NDSolve.
NDSolve does not access the data associated with an algorithm directly, so you can keep the information needed in any form that is convenient or efficient to use. The algorithm and information that might be saved in its private data are accessed only through method functions of the algorithm object.
| AlgorithmObject["Step"[rhs,t,h,y,yp]] | attempt to take a single time step of size h from time t to time  using the numerical algorithm, where y and yp are the approximate solution vector and its time derivative, respectively, at time t; the function should generally return a list using the numerical algorithm, where y and yp are the approximate solution vector and its time derivative, respectively, at time t; the function should generally return a list  where newh is the best size for the next step determined by the algorithm and where newh is the best size for the next step determined by the algorithm and  is the increment such that the approximate solution at time is the increment such that the approximate solution at time  is given by is given by  ; if the time step is too large, the function should only return the value {hnew} where hnew should be small enough for an acceptable step (see later for complete descriptions of possible return values) ; if the time step is too large, the function should only return the value {hnew} where hnew should be small enough for an acceptable step (see later for complete descriptions of possible return values) |
| AlgorithmObject["DifferenceOrder"] | return the current asymptotic difference order of the algorithm |
| AlgorithmObject["StepMode"] | return the step mode for the algorithm object where the step mode should either be Automatic or  ; Automatic means that the algorithm has a means to estimate error and determines an appropriate size newh for the next time step; ; Automatic means that the algorithm has a means to estimate error and determines an appropriate size newh for the next time step;  means that the algorithm will be called from a time step controller and is not expected to do any error estimation means that the algorithm will be called from a time step controller and is not expected to do any error estimation |
Required method functions for algorithms used from NDSolve.
These method functions must be defined for the algorithm to work with
NDSolve. The

method function should always return a list, but the length of the list depends on whether the step was successful or not. Also, some methods may need to compute the function value

at the step end, so to avoid recomputation, you can add that to the list.
| |
{newh,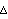 y} y} | successful step with computed solution increment  and recommended next step and recommended next step  |
{newh,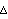 y,yph} y,yph} | successful step with computed solution increment  and recommended next step newh and time derivatives computed at the step endpoint, and recommended next step newh and time derivatives computed at the step endpoint,  |
{newh,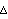 y,yph,newobj} y,yph,newobj} | successful step with computed solution increment  and recommended next step newh and time derivatives computed at the step endpoint, and recommended next step newh and time derivatives computed at the step endpoint,  ; any changes in the object data are returned in the new instance of the method object, newobj ; any changes in the object data are returned in the new instance of the method object, newobj |
{newh,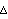 y,None,newobj} y,None,newobj} | successful step with computed solution increment  and recommended next step newh; any changes in the object data are returned in the new instance of the method object, newobj and recommended next step newh; any changes in the object data are returned in the new instance of the method object, newobj |
| {newh} | rejected step with recommended next step newh such that  |
| {newh,$Failed,None,newobj} | rejected step with recommended next step newh such that  ; any changes in the object data are returned in the new instance of the method object, newobj ; any changes in the object data are returned in the new instance of the method object, newobj |
Interpretation of  method output.
method output.
Classical Runge-Kutta
Here is an example of how to set up and access a simple numerical algorithm.
This defines a method function to take a single step toward integrating an ODE using the classical fourth-order Runge-Kutta method. Since the method is so simple, it is not necessary to save any private data.
This defines a method function so that
NDSolve can obtain the proper difference order to use for the method. The

template is used because the difference order for the method is always 4.
This defines a method function for the step mode so that
NDSolve will know how to control time steps. This algorithm method does not have any step control, so you define the step mode to be

.
This integrates the simple harmonic oscillator equation with fixed step size.
| Out[4]= |  |
Generally using a fixed step size is less efficient than allowing the step size to vary with the local difficulty of the integration. Modern explicit Runge-Kutta methods (accessed in
NDSolve with
Method
) have a so-called embedded error estimator that makes it possible to very efficiently determine appropriate step sizes. An alternative is to use built-in step controller methods that use extrapolation. The method

uses an extrapolation based on integrating a time step with a single step of size

and two steps of size

. The method

does a more sophisticated extrapolation and modifies the degree of extrapolation automatically as the integration is performed, but is generally used with base methods of difference orders 1 and 2.
This integrates the simple harmonic oscillator using the classical fourth-order Runge-Kutta method with steps controlled by using the

method.
| Out[5]= |  |
This makes a plot comparing the error in the computed solutions at the step ends. The error for the

method is shown in blue.
| Out[7]= |  |
The fixed step size ended up with smaller overall error mostly because the steps are so much smaller; it required more than three times as many steps. For a problem where the local solution structure changes more significantly, the difference can be even greater.
A facility for stiffness detection is described within
"DoubleStep Method for NDSolve".
For more sophisticated methods, it may be necessary or more efficient to set up some data for the method to use. When
NDSolve uses a particular numerical algorithm for the first time, it calls an initialization function. You can define rules for the initialization that will set up appropriate data for your method.
| InitializeMethod[Algorithm Identifier,stepmode,state,Algorithm Options] |
| the expression that NDSolve evaluates for initialization when it first uses an algorithm for a particular integration where stepmode is either Automatic or  depending on whether your method is expected to be called within the framework of a step controller or another method or not; state is the depending on whether your method is expected to be called within the framework of a step controller or another method or not; state is the  object used by NDSolve, and object used by NDSolve, and  is a list that contains any options given specifically with the specification to use the particular algorithm, for example, {opts} in Method is a list that contains any options given specifically with the specification to use the particular algorithm, for example, {opts} in Method |
| Algorithm Identifier/:InitializeMethod[Algorithm Identifier,stepmode_,rhs_NumericalFunction,state_NDSolveState,{opts___?OptionQ}]:=initialization |
| definition of the initialization so that the rule is associated with the algorithm, and initialization should return an algorithm object in the form  |
Initializing a method from NDSolve.
As a system symbol,

is protected, so to attach rules to it, you would need to unprotect it first. It is better to keep the rules associated with your method. A tidy way to do this is to make the initialization definition using
TagSet as shown earlier.
As an example, suppose you want to redefine the Runge-Kutta method shown earlier so that instead of using the exact coefficients 2, 1/2, and 1/6, numerical values with the appropriate precision are used instead to make the computation slightly faster.
This defines a method function to take a single step toward integrating an ODE using the classical fourth-order Runge-Kutta method using saved numerical values for the required coefficients.
This defines a rule that initializes the algorithm object with the data to be used later.
Saving the numerical values of the numbers gives between 5 and 10 percent speedup for a longer integration using

.
Adams Methods
In terms of the
NDSolve framework, it is not really any more difficult to write an algorithm that controls steps automatically. However, the requirements for estimating error and determining an appropriate step size usually make this much more difficult from both the mathematical and programming standpoints. The following example is a partial adaptation of the Fortran DEABM code of Shampine and Watts to fit into the
NDSolve framework. The algorithm adaptively chooses both step size and order based on criteria described in [
SG75].
The first stage is to define the coefficients. The integration method uses variable step-size coefficients. Given a sequence of step sizes

, where

is the current step to take, the coefficients for the method with Adams-Bashforth predictor of order

and Adams-Moulton corrector of order

,

such that
where the

are the divided differences.
This defines a function that computes the coefficients

and

, along with

, that are used in error estimation. The formulas are from [
HNW93] and use essentially the same notation.
hlist is the list of step sizes

from past steps. The constant-coefficient Adams coefficients can be computed once, and much more easily. Since the constant step size Adams-Moulton coefficients are used in error prediction for changing the method order, it makes sense to define them once with rules that save the values.
This defines a function that computes and saves the values of the constant step size Adams-Moulton coefficients.
The next stage is to set up a data structure that will keep the necessary information between steps and define how that data should be initialized. The key information that needs to be saved is the list of past step sizes,
hlist, and the divided differences,

. Since the method does the error estimation, it needs to get the correct norm to use from the
NDSolve`StateData object. Some other data such as precision is saved for optimization and convenience.
This defines a rule for initializing the

method from
NDSolve.
hlist is initialized to

since at initialization time there have been no steps.

is initialized to the derivative of the solution vector at the initial condition since the 0

divided difference is just the function value. Note that

is a matrix. The third element, which is initialized to a zero vector, is used for determining the best order for the next step. It is effectively an additional divided difference. The use of the other parts of the data is clarified in the definition of the stepping function.
The initialization is also set up to get the value of an option that can be used to limit the maximum order of the method to use. In the code DEABM, this is limited to 12, because this is a practical limit for machine-precision calculations. However, in
Mathematica, computations can be done in higher precision where higher-order methods may be of significant advantage, so there is no good reason for an absolute limit of this sort. Thus, you set the default of the option to be

.
This sets the default for the

option of the

method.
Before proceeding to the more complicated

method functions, it makes sense to define the simple

and

method functions.
This defines the step mode for the

method to always be
Automatic. This means that it cannot be called from step controller methods that request fixed step sizes of possibly varying sizes.
This defines the difference order for the

method. This varies with the number of past values saved.
Finally, here is the definition of the

function. The actual process of taking a step is only a few lines. The rest of the code handles the automatic step size and order selection following very closely the DEABM code of Shampine and Watts.
This defines the

method function for

that returns step data according to the templates described earlier.
There are a few deviations from DEABM in the code here. The most significant is that coefficients are recomputed at each step, whereas DEABM computes only those that need updating. This modification was made to keep the code simpler, but does incur a clear performance loss, particularly for small to moderately sized systems. A second significant modification is that much of the code for limiting rejected steps is left to
NDSolve, so there are no checks in this code to see if the step size is too small or the tolerances are too large. The stiffness detection heuristic has also been left out. The order and step-size determination code has been modularized into separate functions.
This defines a function that constructs error estimates

for

,

, and

and determines if the order should be lowered or not.
This defines a function that determines the best order to use after a successful step.
This defines a function that determines the best step size to use after a successful step of size

.
Once these definitions are entered, you can access the method in
NDSolve by simply using
Method
.
This solves the harmonic oscillator equation with the Adams method defined earlier.
| Out[29]= |  |
This shows the error of the computed solution. It is apparent that the error is kept within reasonable bounds. Note that after the first few points, the step size has been increased.
| Out[30]= |  |
Where this method has the potential to outperform some of the built-in methods is with high-precision computations with strict tolerances. This is because the built-in methods are adapted from codes with the restriction to order 12.
A lot of time is required for coefficient computation.
| Out[33]= |  |
This is not using as high an order as might be expected.
In any case, about half the time is spent generating coefficients, so to make it better, you need to figure out the coefficient update.
| Out[34]= |  |