I am trying to get a better understanding of kernel density estimation.
Using the definition from Wikipedia: https://en.wikipedia.org/wiki/Kernel_density_estimation#Definition
$ \hat{f_h}(x) = \frac{1}{n}\sum_{i=1}^n K_h (x - x_i) \quad = \frac{1}{nh} \sum_{i=1}^n K\Big(\frac{x-x_i}{h}\Big) $$$ \hat{f_h}(x) = \frac{1}{n}\sum_{i=1}^n K_h (x - x_i) \quad = \frac{1}{nh} \sum_{i=1}^n K\Big(\frac{x-x_i}{h}\Big) $$
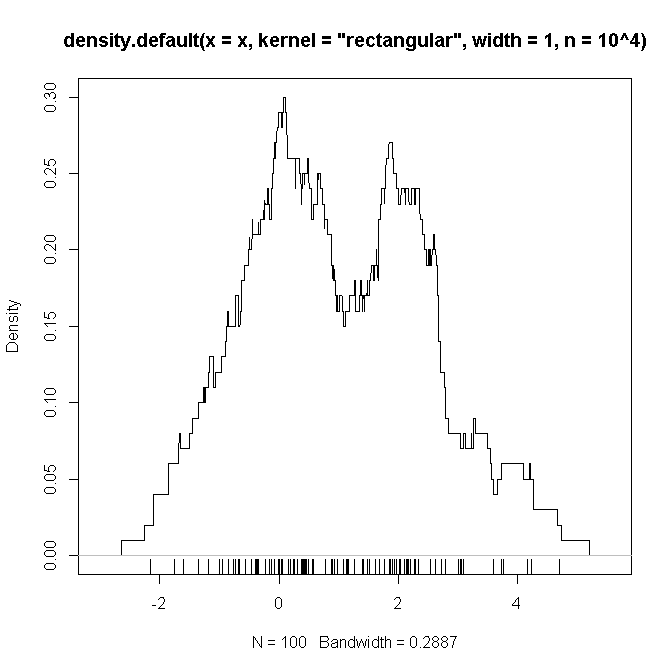
Let's take $K()$ to be a rectangular function which gives $1$ if $x$ is between $-0.5$ and $0.5$ and $0$ otherwise, and $h$ (window size) to be 1.
I understand that the density is a convolution of two functions, but I am not sure I know how to define these two functions. One of them should (probably) be a function of the data which, for every point in R, tells us how many data points we have in that location (mostly $0$). And the other function should probably be some modification of the kernel function, combined with the window size. But I am not sure how to define it.
Any suggestions?
Bellow is an example R code which (I suspect) replicates the settings I defined above (with a mixture of two Gaussians and $n=100$), on which I hope to see a "proof" that the functions to be convoluted are as we suspect.
# example code: set.seed(2346639) x <- c(rnorm(50), rnorm(50,2)) plot(density(x, kernel='rectangular', width=1, n = 10**4)) rug(x)