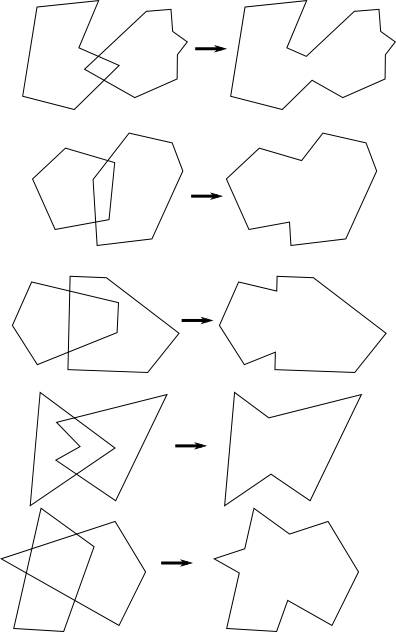
Union of Two Polygons
Given two intersecting polygons as input, output a third polygon that is the union of the two input polygons, that is to say, the perimeter that encloses all points present in at least one of the two input polygons.
Example inputs/outputs
2 Squares
[(0, 0), (0, 2), (2, 2), (2, 0)] | [(1, 1), (1, 3), (3, 3), (3, 1)] ==> [(0, 0), (0, 2), (1, 2), (1, 3), (3, 3), (3, 1), (2, 1), (2, 0)] ... more to come
Notes and Rules
- Input will be two lists of at least 3 2d points each, taken in any convenient format.
- Output should be a list of 2d points, in any convenient format.
- It does not matter which point you list first.
- It does not matter whether you output in clockwise or counterclockwise order.
- Polygons may be concave
- You may assume that both polygons are not self-intersecting
- You may assume that the polygons overlap in at least two places exclusively via edge-edge crossings rather than vertex-edge intersections, vertex-vertex intersections, or flush edge-edge overlaps.
- You may assume that the polygons do not overlap in such a way that the union would have at least one hole in it.
- You must be accurate to at least 0.01 for all polygons between -100 and 100 units along each axis.
- Standard rules apply. Shortest code wins.