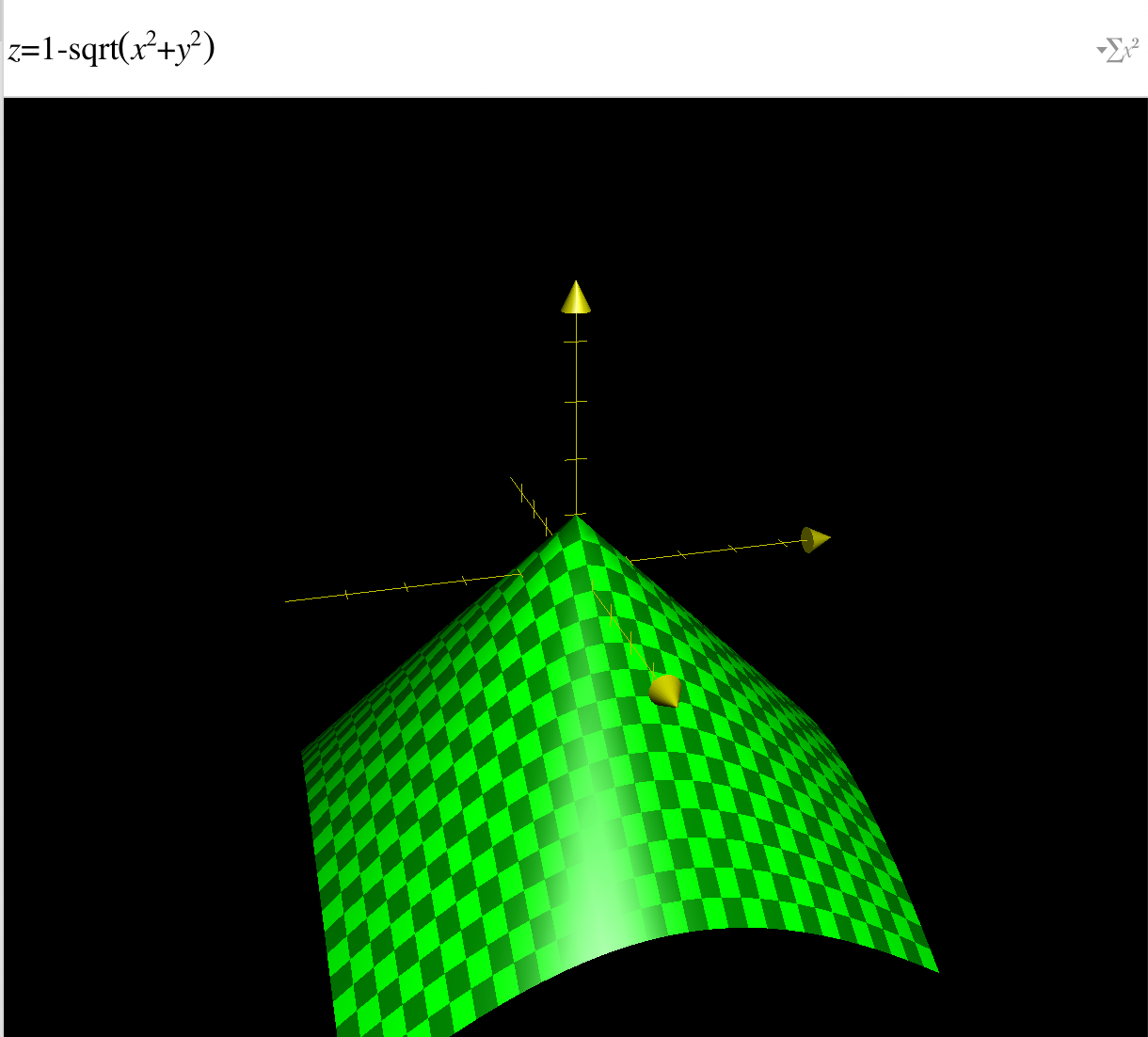
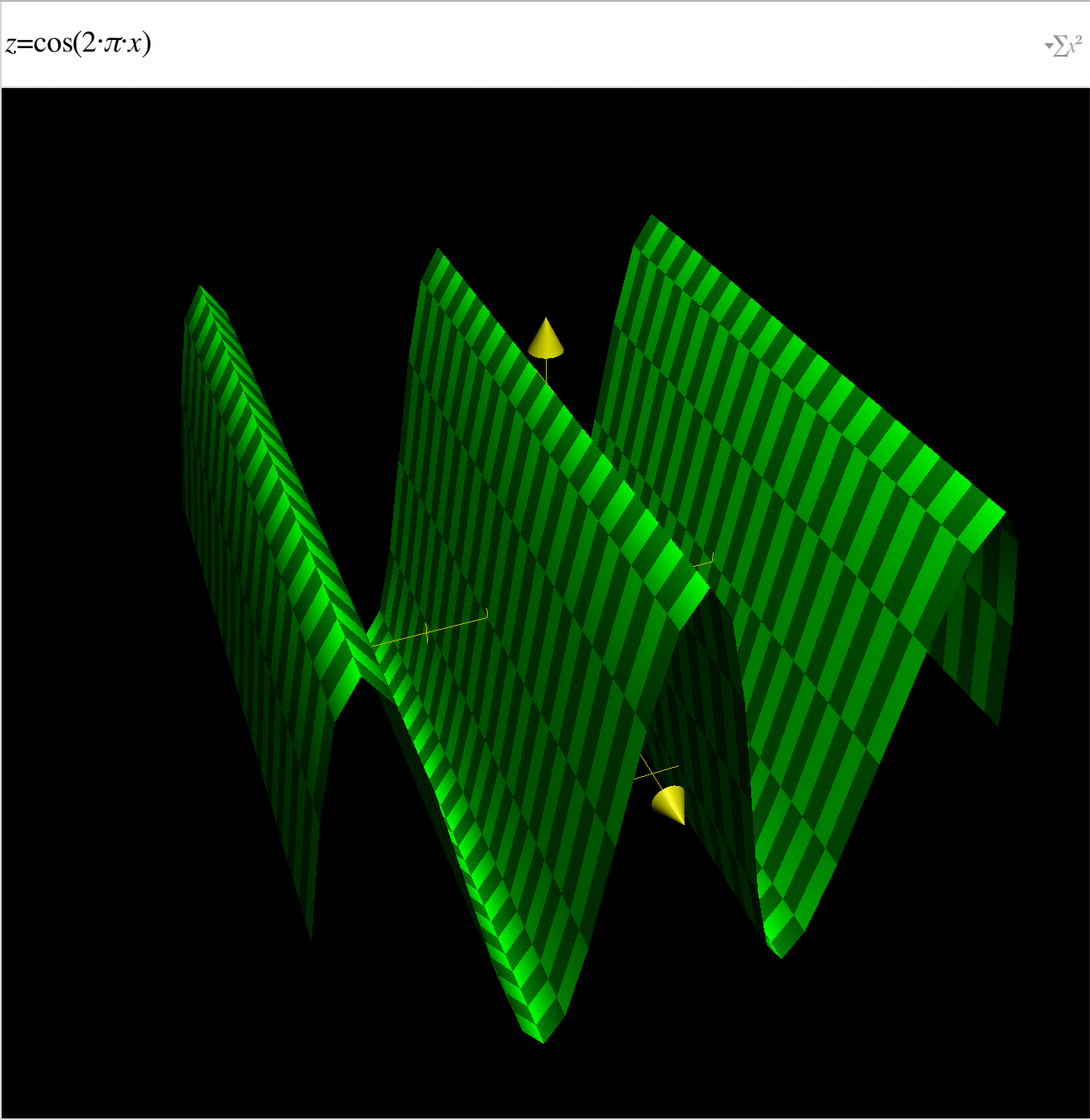
This is a screen shot from an animation generated by a matplotlib example
the key part in the code is
R = 1 - np.sqrt(X**2 + Y**2) Z = np.cos(2 * np.pi * X + phi) * R corresponding equation is
$\left(- \sqrt{X^{2} + Y^{2}} + 1\right) \cos{\left (2 \pi X + \phi \right )}$
Could some give an explanation or hint about this kind of equation?
Is there a name of this type of graphics?
usually cosine/sine could generate something like a (half) circle, what does R part do?
The R part generates a cone where the point is at (0, 0, 1) and it spreads out below that. It meets the x-y plane at the unit circle:
The cos component defines an extruded cosine wave along the X-axis:
So the final equation takes the cosine wave and multiplies its amplitude by the cone. It will have full amplitude at the origin, and decrease to 0 at the unit circle on the x-y plane. Past that it becomes negative:
The phi component shifts the sine wave forward or backward along the x axis.
