2
$\begingroup$

The document I am reading is here: Turing Machines

Before getting into the question, here is the notation used on the picture:

Here $\Delta$ denotes the blank and R, L and S denote move the head right, left and do not move it, respectively. A transition diagram can also be drawn for a Turing machine. The states are represented by vertices and for a transition $\delta( q, X ) = ( r, Y, D )$ , where D represents R, L or S , an arc from q to r is drawn with label ( X/Y , D ) indicating that the state is changed from q to r, the symbol X currently being read is changed to Y and the tape head is moved as directed by D.

According to the document:

A Turing machine T is said to decide a language L if and only if T writes "yes" and halts if a string is in L and T writes "no" and halts if a string is not in L

Here is the three examples:

  • Case 1:

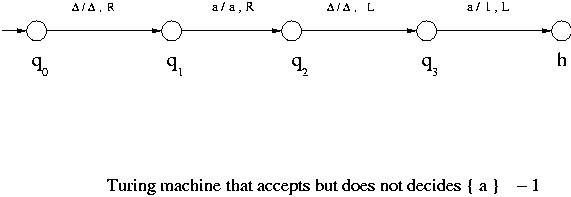
Case 1

  • Case 2:

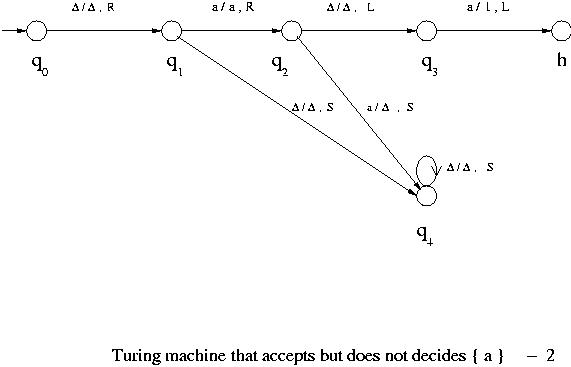
Case 2

  • Case 3:

Case 3

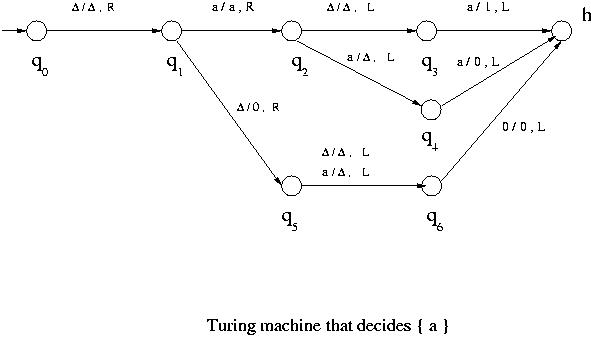
I just want to verify my understanding. According to the definition, in case 1 and case 2, its turing machines cannot decide because the machines cannot tell whether invalid inputs rather than { a } (such as aa, aaa, aaaa....) is in L or not.

In case 2, if another a appears after the first a, or if the input is empty, the machine goes to state S and loop forever.

In case 3, if a is detected and only a single a exists, that a is replaced by 1 and the machine accepts. Otherwise, a 0 is replaced and the input is decided not in the language.

Am I correct on all of these? However, in case 3, what if I give any input which contains other character rather than a (such as string ab, bc...)? Or is it said that TM decides only languages over a set of alphabet $\Sigma$ allowed by the Turing Machine?

If a string which is longer than a single a (like aa, aaa,ab,bc...), the machine may loop forever (like in case 2) or halt without accepting (in other words, it is "crashed", where it does not have transition rules for a symbol in the input such as b in the case of above Turing Machines). Is this correct also?

Improve this question
$\endgroup$
5
  • $\begingroup$ Other definitions of Turing machines generally do not require the TM to write "yes" or "no". Entering an accepting or rejecting state is sufficient. (Definitions are equivalent, though). "Crashed" is not standard terminology, and is misleading – "rejected" is better. $\endgroup$ Commented Jun 4, 2012 at 6:12
  • $\begingroup$ I am confused by the first transistions. Typically, a TM starts on the first input symbol, i.e. $\neq \Delta$ for non-empty inputs, so those TMs won't accept anything. Sadly, the document does not specify the semantics very carefully; have you checked other texts? $\endgroup$ Commented Jun 4, 2012 at 8:38
  • $\begingroup$ Yes, I learned it after my lecture. I read the text for more concrete examples. I still wonder what happens if the input contains symbols other than what is defined in a given alphabet. Halt and reject, maybe? $\endgroup$ Commented Jun 4, 2012 at 9:14
  • 1
    $\begingroup$ @Amumu: That can't happen by definition. That's the beauty of theory: closed world is not an assumption, but fact. In other words, the semantics of Turing machines are not even defined for words over an alphabet other than the TM's. $\endgroup$ Commented Jun 5, 2012 at 11:07
  • $\begingroup$ @Raphael Thanks for introducing the subject. Now it even makes more sense. $\endgroup$ Commented Jun 5, 2012 at 19:49

1 Answer 1

Reset to default
8
$\begingroup$

A TM decides a language if it enters the accepting state for word in the language and it enters the rejecting state if it is not. Thus it halts on all inputs. Note the machines defined above are not entirely standard. They way they denote acceptance and reject is by writing a $1$ or $0$ and then by entering a halting state. This is equivalent to the standard definition, but less elegant.

Machine 1 does not reject words not in the language. It only accepts the language.

Machine 2 does not halt for words not in the language. It only accepts the language.

Machine 3 rejects and hence halts for words not in the language, therefore it decides the language.

Improve this answer
$\endgroup$
7
  • $\begingroup$ Thanks for your confirmation. However, machine 3 rejects input only if the input is empty (blank at the start of the input), as you can see in the diagram for machine 3. What if the input is anything rather than a or blank? (such as b. I don't see a state where it handles b. The delta notation (triangle) only denotes a blank). $\endgroup$ Commented Jun 4, 2012 at 6:56
  • $\begingroup$ I don't think that $b$ is even in the alphabet. Also, the machine writes a $0$ or $1$ on the tape to indicate success or failure, which is quite nonstandard. I would find another resource to learn about Turing Machines. For example, the book "Introduction to the Theory of Computation" by Michael Sipser, is excellent. $\endgroup$ Commented Jun 4, 2012 at 7:30
  • $\begingroup$ Well, suppose an arbitrary input contains b is read by a machine which only accepts input over a set of alphabet {a} (like the 3 machines above). I think the machines will halt and reject since it has not transition. However, if it is the case, then isn't machine one sufficient enough? I mean, even if the input only contains a but more than one, machine 1 will still halt and reject anything not in L. Why do we even need machine 3 to handle additional cases? $\endgroup$ Commented Jun 4, 2012 at 7:46
  • 1
    $\begingroup$ A TM is defined over a given alphabet, not over an arbitrary alphabet. The words are defined over the given alphabet. A Turing Machine needs to explicitly reject by (in this case) writing a 0 on the tape. It cannot implicitly reject. My advice is to find better notes to learn from. $\endgroup$ Commented Jun 4, 2012 at 7:54
  • 2
    $\begingroup$ The machine is defined over a given alphabet. So the question of what the machine does for a symbol outside the alphabet does not make sense. It's like asking what is the meaning of passing a C program to a Java compiler. $\endgroup$ Commented Jun 4, 2012 at 10:57

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.