The previous answers give pretty much the explanation, though mostly from a pragmatic angle, for as much as the question makes sense, as excellently explained by Raphael's answer.
Adding to this answer, we should note that, nowadays, C compilers are written in C. Of course, as noted by Raphael their output and its performance may depend, among other things, on the CPU it is running on. But it also depends on the amount of optimization done by the compiler. If you write in C a better optimizing compiler for C (which you then compile with the old one to be able to run it), you get a new compiler that makes C a faster language than it was before. So, what is the speed of C? Note that you can even compile the new compiler with itself, as a second pass, so that it compiles more efficiently, though still giving the same object code. And the full employment theorem shows that their is no end to such improvements (thanks to Raphael for the pointer).
But I think it may be worthwhile trying to formalize the issue, as it illustrate very well some fundamental concepts, and particularly denotational versus operational view of things.
What is a compiler?
A compiler $C_{S\to T}$, abbreviated to $C$ if there is no ambiguity, is a realization of a computable function $\mathcal C_{S\to T}$ that will translate a program text $P_{:S}$ computing a function $\mathcal P$, written in a source language $S$ into program text $P_{:T}$ written in a target language $T$, that is supposed to compute the same function $\mathcal P$.
From a semantic point of view, i.e. denotationally, it does not matter how this compiling function $\mathcal C_{S\to T}$ is computed, i.e., what realization $C_{S\to T}$ is chosen. It could even be done by a magic oracle. Mathematically, the function is simply a set of pairs $\{(P_{:S},P_{:T})\mid P_S\in S \wedge P_T\in T\}$.
The semantic compiling function $\mathcal C_{S\to T}$ is correct if both $P_S$ and $P_T$ compute the same function $\mathcal P$. But this formalization applies as well to an incorrect compiler. The only point is that whatever is implemented achieves the same result independently of the implementation means. What matters semantically is what is done by the compiler, not how (and how fast) it is done.
Actually getting $P_{:T}$ from $P_{:S}$ is an operational issue, that must be solved. This is why the compiling function $\mathcal C_{S\to T}$ must be a computable function. Then any language with Turing power, no matter how slow, is sure to be able to produce code as efficient as any other language, even if it may do so less efficiently.
Refining the argument, we probably want the compiler to have good efficiency, so that the translation can be performed in reasonable time. So the performance of the compiler program matters for users, but it has no impact on semantics. I am saying performance, because the theoretical complexity of some compilers can be much higher than one would expect.
About bootstrapping
This will illustrate the distinction, and show a practical application.
It is now common place to first implement a language $S$ with an interpreter $I_S$, and then write a compiler $C_{S\to T\,:S}$ in the language $S$ itself. This compiler $C_{S\to T\,:S}$ can be run with the interpreter $I_S$ to translate any program $P_{:S}$ into a program $P_{:T}$. So we do have a running compiler from language $S$ to (machine?) language $T$, but it is very slow, if only because it runs on top of an interpreter.
But you can use this compiling facility to compile the compiler $C_{S\to T\,:S}$, since it is written in language $S$, and thus you get a compiler $C_{S\to T\,:T}$ written in the target language $T$. If you assume, as often the case, that $T$ is a language that is more efficiently interpreted (machine native, for example), then you get a faster version of your compiler running directly in language $T$. It does exactly the same job (i.e. produces the same target programs), but it does it more efficiently.
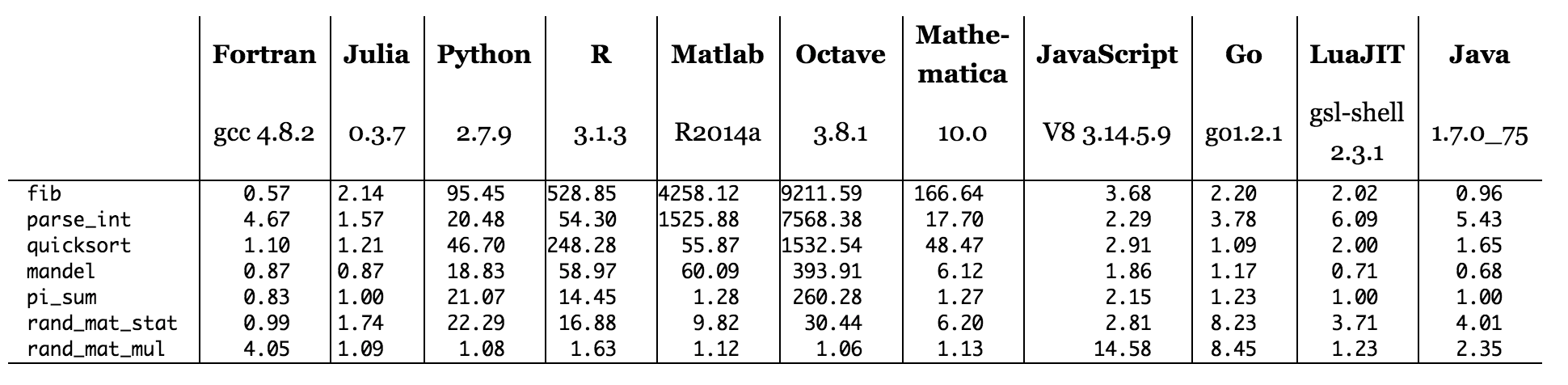 Figure: benchmark times relative to C (smaller is better, C performance = 1.0).
Figure: benchmark times relative to C (smaller is better, C performance = 1.0).