Unless you have a very good reason to use an ensemble inside the iterative imputer I would highly recommend to change the base estimator.
As mentioned on the previous answer, you can limit the tree's depth or change the max_features parameter to sqrt (both improve the execution time in ~20%) at the cost of prediction quality, but again the same question lies, is it necessary to use an ensemble inside the imputer or can a simpler model give good results with much lower cost?
So we can mention 2 options (no the only ones):
- change the base estimator
- Keep the same imputer (regularizing via the
max_depth and max_features) and training it in a sample of your data for then make the imputation on all your data
I replicated this example from scikit-learn documentation and the time of ExtraTreeRegressor was ~16x greater as compared with the default BayessianRidgeRegressor even when using only 10 estimators (when trying with 100 it did not even finish)
I also tried using other kind of ensembles and the time is also reduced significantly as compered with ExtraTreeRegressor
I recommend you to make a similar analysis using you data and see the real impact on model's performance (try using a sample of your data) for each alternative.
In conclusion I would go for another less expensive base estimator from a cost-benefit perspective.
%%time import numpy as np import matplotlib.pyplot as plt import pandas as pd import warnings warnings.filterwarnings("ignore") # To use this experimental feature, we need to explicitly ask for it: from sklearn.experimental import enable_iterative_imputer # noqa from sklearn.datasets import fetch_california_housing from sklearn.impute import SimpleImputer from sklearn.impute import IterativeImputer from sklearn.linear_model import BayesianRidge from sklearn.tree import DecisionTreeRegressor from sklearn.ensemble import ExtraTreesRegressor from sklearn.neighbors import KNeighborsRegressor from sklearn.pipeline import make_pipeline from sklearn.model_selection import cross_val_score from sklearn.ensemble import GradientBoostingRegressor from lightgbm import LGBMRegressor from time import time N_SPLITS = 5 rng = np.random.RandomState(0) X_full, y_full = fetch_california_housing(return_X_y=True) # ~2k samples is enough for the purpose of the example. # Remove the following two lines for a slower run with different error bars. X_full = X_full[::10] y_full = y_full[::10] n_samples, n_features = X_full.shape # Estimate the score on the entire dataset, with no missing values br_estimator = BayesianRidge() score_full_data = pd.DataFrame( cross_val_score( br_estimator, X_full, y_full, scoring='neg_mean_squared_error', cv=N_SPLITS ), columns=['Full Data'] ) # Add a single missing value to each row X_missing = X_full.copy() y_missing = y_full missing_samples = np.arange(n_samples) missing_features = rng.choice(n_features, n_samples, replace=True) X_missing[missing_samples, missing_features] = np.nan # Estimate the score after imputation (mean and median strategies) score_simple_imputer = pd.DataFrame() for strategy in ('mean', 'median'): estimator = make_pipeline( SimpleImputer(missing_values=np.nan, strategy=strategy), br_estimator ) score_simple_imputer[strategy] = cross_val_score( estimator, X_missing, y_missing, scoring='neg_mean_squared_error', cv=N_SPLITS ) # Estimate the score after iterative imputation of the missing values # with different estimators estimators = [ BayesianRidge(), DecisionTreeRegressor(max_features='sqrt', random_state=0), ExtraTreesRegressor(n_estimators=10, random_state=0), KNeighborsRegressor(n_neighbors=15), GradientBoostingRegressor(n_estimators= 10, random_state= 0), LGBMRegressor(n_estimators=10,random_state=0) ] score_iterative_imputer = pd.DataFrame() for impute_estimator in estimators: t0 = time() estimator = make_pipeline( IterativeImputer(random_state=0, estimator=impute_estimator), br_estimator ) score_iterative_imputer[impute_estimator.__class__.__name__] = \ cross_val_score( estimator, X_missing, y_missing, scoring='neg_mean_squared_error', cv=N_SPLITS ) print(f"Time for estimator: {impute_estimator.__class__.__name__} is {round(time() - t0,3)} seconds") scores = pd.concat( [score_full_data, score_simple_imputer, score_iterative_imputer], keys=['Original', 'SimpleImputer', 'IterativeImputer'], axis=1 ) # plot california housing results fig, ax = plt.subplots(figsize=(13, 6)) means = -scores.mean() errors = scores.std() means.plot.barh(xerr=errors, ax=ax) ax.set_title('California Housing Regression with Different Imputation Methods') ax.set_xlabel('MSE (smaller is better)') ax.set_yticks(np.arange(means.shape[0])) ax.set_yticklabels([" w/ ".join(label) for label in means.index.tolist()]) plt.tight_layout(pad=1) plt.show()
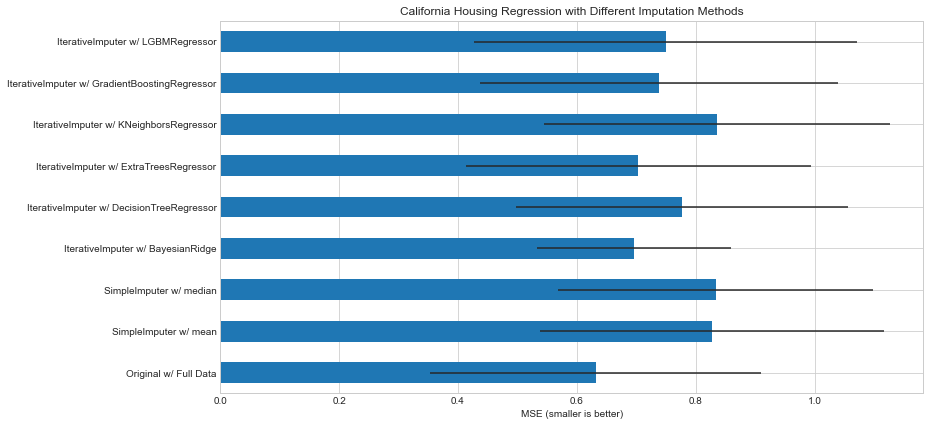
Time for estimator: BayesianRidge is 1.149 seconds Time for estimator: DecisionTreeRegressor is 2.629 seconds Time for estimator: ExtraTreesRegressor is 17.02 seconds Time for estimator: KNeighborsRegressor is 1.73 seconds Time for estimator: GradientBoostingRegressor is 11.442 seconds Time for estimator: LGBMRegressor is 7.169 seconds

