0
$\begingroup$

My question is on OFDM signals for LTE. I been reading a tutorial on LTE where ofcourse the modulation is OFDM and it is explained that an OFDM signal is a rect function in time domain. The duration is equal to $\frac{1}{\Delta f}$ assuming ${\Delta f}$ is the subcarrier spacing. Then it is explained that in frequency domain the subcarriers will have sinc func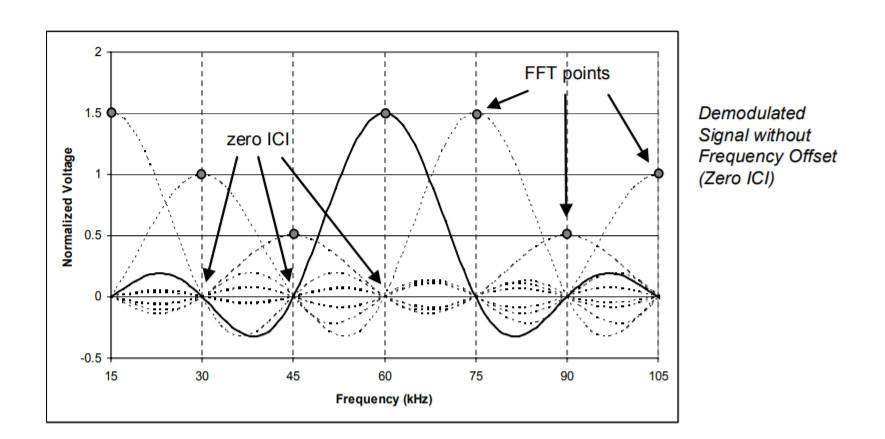enter image description here (see figure above) and that the crossings are at integer multiples of the subcarrier frequencies $k \Delta f$

I was then looking for the Power spectral density of OFDM signal. And somewhere it is mentioned that it should look like this 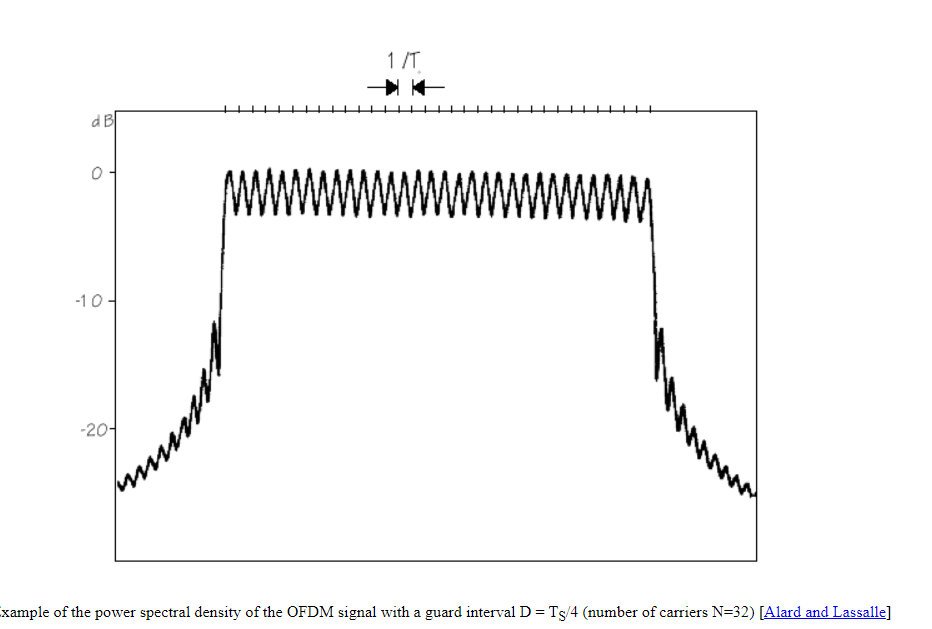enter image description here

I have no idea why the PSD of sinc function will end up being looking like what is presented in the second figure. Isnt the PSD just the absolute value of the signal in frequency domain squared?

How do you go from sinc to this PSD. Hope someone can help.

Thanks,

Improve this question
$\endgroup$
1
  • $\begingroup$ OFDM is comprised of multiple Sinc functions spaced closely together in frequency, not just one. This response at this post may help answer your question: dsp.stackexchange.com/questions/74087/… $\endgroup$ Commented Jun 3, 2021 at 1:23

1 Answer 1

Reset to default
0
$\begingroup$

it is explained that an OFDM signal is a rect function in time domain

No, be careful here: each subcarrier has rect shape, so the ofdm signal is the sum of rect functions, each modulated with a different complex sinusoid, shifting it in frequency.

Then it is explained that in frequency domain the subcarriers will have sinc func

Exactly, each subcarrier has sinc shape, but is shifted to a different frequency.

I have no idea why the PSD of sinc function will end up being looking like what is presented in the second figure.

It's not a single sinc, but the sum of many sincs, shifted as shown in your first figure.

Improve this answer
$\endgroup$

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.