1
$\begingroup$

I need to find the phase difference between two sinusoidal signals with the same frequency (23.5MHz) but not in same phase.

Test case:

  • Generate two sinusoidal signals of length 8 with different phases (signal 1 has 0degree phase and signal 2 has 90 degree phase) from a Xilinx DDS compiler IP core.
  • The two signals are given to separate FFT IP cores which give the corresponding real and imaginary values.
  • The real and imaginary values at the 2nd bin are given as input to a Cordic Ip core (arctan function) to find the phase angle of each signal. The output format of the two cordic Ip cores is in radians, so we multiply the output by $180/\pi$.
  • The two phase angles of the signals are then subtracted to get the phase difference but we are getting the wrong value.
Improve this question
$\endgroup$
0

2 Answers 2

Reset to default
4
$\begingroup$

Unless your sine wave frequency is an integer multiple of your frequency resolution (sample rate divided by FFT length), this will not work. Spectral analysis using an FFT is quite complicated. Look for "spectral leakage" on this forum (or Google it) for more explanations.

You don't need an FFT to determine the phase difference. Let's say you have two sine waves

$$x_1(t) = A_1\cos(\omega_0t+\phi_1) \\x_2(t) = A_2\cos(\omega_0t+\phi_2)$$

If you multiply them, you get

$$y(t) = x_1(t) \cdot x_2(t) = A_1A_2\cos(\omega_0t+\phi_1)\cos(\omega_0t+\phi_2) $$

Using a trigonometric identity we get

$$y(t) = \frac{1}{2}\left[\cos(2\omega_0 t+\phi_1+\phi_2)+\cos(\phi_1-\phi_2) \right]$$

There is a constant offset that's a function of the phase difference, i.e. you can get the difference from the mean of the multiplied signal,

$$ \phi_1-\phi_2 = \cos^{-1}\left(\frac{\langle y(t) \rangle}{A_1A_2}\right)$$

For only 8 points you may get some numerical noise, but that depends a bit on your details and the sample rate.

Improve this answer
$\endgroup$
2
  • $\begingroup$ you have to know which of $\phi_1$ or $\phi_2$ are leading. there is a $\pm$ ambiguity. $\endgroup$ Commented Aug 16, 2022 at 15:37
  • $\begingroup$ From your identity, you're missing a factor of two: $\Delta\phi=\cos^{-1}\left(2\left \langle y(t) \right \rangle / A_1A_2\right)$ $\endgroup$ Commented Mar 23, 2023 at 7:09
-1
$\begingroup$ 
close all;clear all;clc % MATLAB script available by email [email protected]

1.- Simulating 2 random phases

ph1_deg=.1*(2*(randi([1 2],1,1)-1.5))*randi([150 1800],1,1) ph2_deg=.1*(2*(randi([1 2],1,1)-1.5))*randi([150 1800],1,1) ph1=ph1_deg*pi/180 ph2=ph2_deg*pi/180 dph=abs(ph1-ph2) dph_deg=dph*180/pi

2.- Generating signals

same carrier 2 random different phases within [15 180]deg

f1=23.5e6 % [Hz] T1=1/f1 fs=100*f1; dt=1/fs; amount_cycles_measured=5 t=[0:dt:amount_cycles_measured*T1]; x1=sin(2*pi*f1*t+ph1); x2=sin(2*pi*f1*t+ph2); figure(1) plot(t,x1,t,x2) grid on xlabel('t') title('x1 x2')

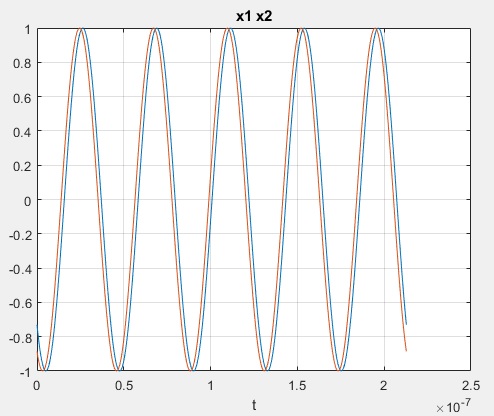
enter image description here

3.- So far so good, one checks a trigonometry manual and there you have it : Multiply both carriers and the phase difference should readily come up.

But the resulting theoretical expression is supposed to be time independent, it's supposed to be DC.

In RF boards DC is almost always blocked preventing access into different RF stages.

Shure Xilinx boards have some DC protection to prevent DC hitting signal processing modules.

x12=x1.*x2; figure(2) plot(t,(x12)) grid on xlabel('t') title('x1*x2')

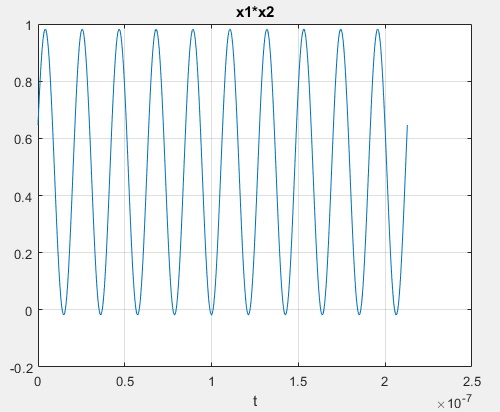
enter image description here

wasn't this supposed to be a clear measurement of the phase difference?

perhaps the power of the difference

figure(3) plot(t,(x1-x2).^2) grid on xlabel('t') title('(x1-x2)^2')

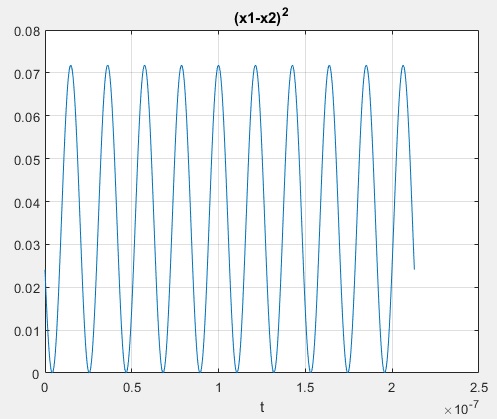
enter image description here

4.- There's a clear loss of amplitude accuracy, the amplitude that has to supply the DC reading for the phase difference.

May be another difference of powers?

x3=x1.^2; x4=x2.^2; x34=abs(x3-x4); figure(4) plot(t,x34) grid on xlabel('t') title('|x1^2-x2^2|')

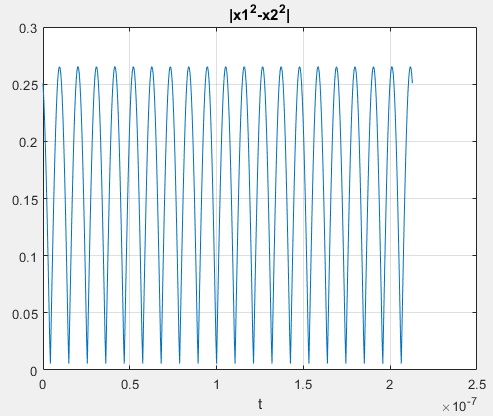
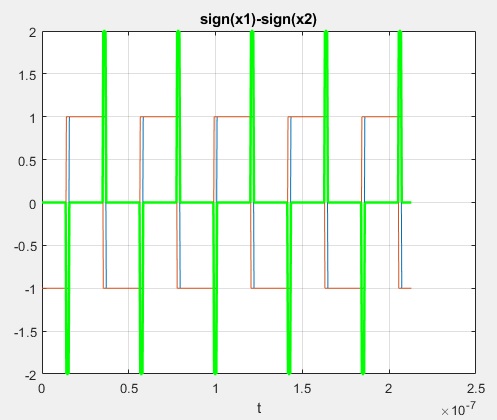
enter image description here

5.- Let's focus on the zero crossings

x5=sign(x1); x6=sign(x2); x56=x5-x6; figure(5) plot(t,x5,t,x6) hold on plot(t,x56,'g','LineWidth',2) grid on xlabel('t') title('sign(x1)-sign(x2)')

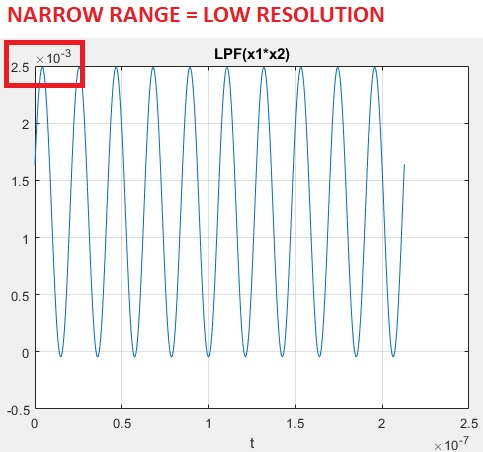
enter image description here

6.- Perhpaps Low Pass Filtering x1.*x2 increases DC accuracy?

sr = dsp.SignalSource; sr.Signal = x12; sink = dsp.SignalSink; nth=20 % filter order wsn=.25 % normalized Nyquist freq = fs/2 fir = dsp.FIRFilter(fir1(nth,wsn)); % .25 fraction of Nyquist freq sa = dsp.SpectrumAnalyzer('SampleRate',fs,... 'PlotAsTwoSidedSpectrum',false,... 'OverlapPercent', 80, 'PowerUnits','dBW',... 'YLimits', [-150 -10]); while ~isDone(sr) input = sr(); filteredOutput = fir(input); sink(filteredOutput); end filteredResult = sink.Buffer; % fvtool(fir,'Fs',f1/2) figure(6) plot(t,filteredResult) grid on xlabel('t') title('LPF(x1*x2)')

enter image description here

filter used enter image description here

Low Pass Filtered signal containing the phase difference does not show the expected accuracy to measure phase differences.

And this is without noise.

Observe that the peak value is 2.5e-3 .

To measure with precision a phase difference it is convenient to work with for instance a [0 5]V range, not with mV if possible.

7.- Squaring input signals

x56(x56<0)=0; x56=.5*x56; figure(7) plot(t,x56) hold on plot(t,x56,'g','LineWidth',3) grid on xlabel('t') title('sign(x1)-sign(x2)')

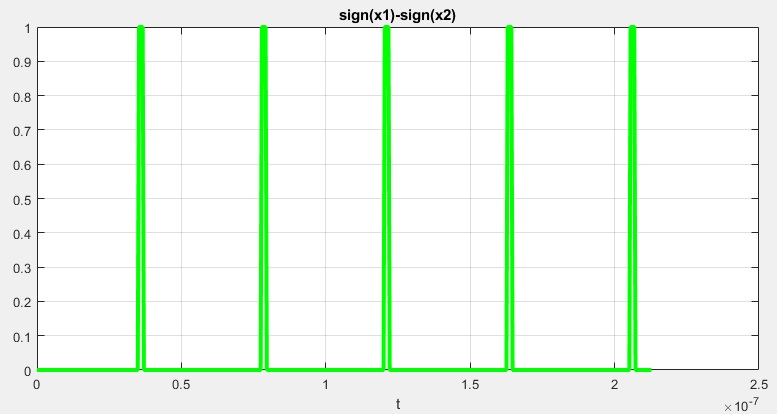
enter image description here

All that's left is to measure pulse widths, perhaps average a few of them and translate pulsewidth (time) to phase (difference)

Do not demodulate to DC.

All you need are the difference between squared input signals

d1_deg=360*numel(x56(x56==0))/numel(x56) if d1_deg>180 d1_deg=360-d1_deg; end

comparing

d1_deg = 14.371257485029957 dph_deg = 15.099999999999991

d1_deg is measured phase difference and dph_deg is expected value.

absolute error

err_abs=abs(d1_deg-dph_deg) = 0.728742514970033

relative error

err_rel=err_abs/dph_deg*100 = 4.826109370662475

8.- Example MFJ222 phase difference meter [1 50] MHz Manufactured by MFJ Enterprises, 300 Industrial Park Road, Starkville, MS 39759. Phone: (662) 323-5869

MFJ schematic (public, available online) showing signals conditioning

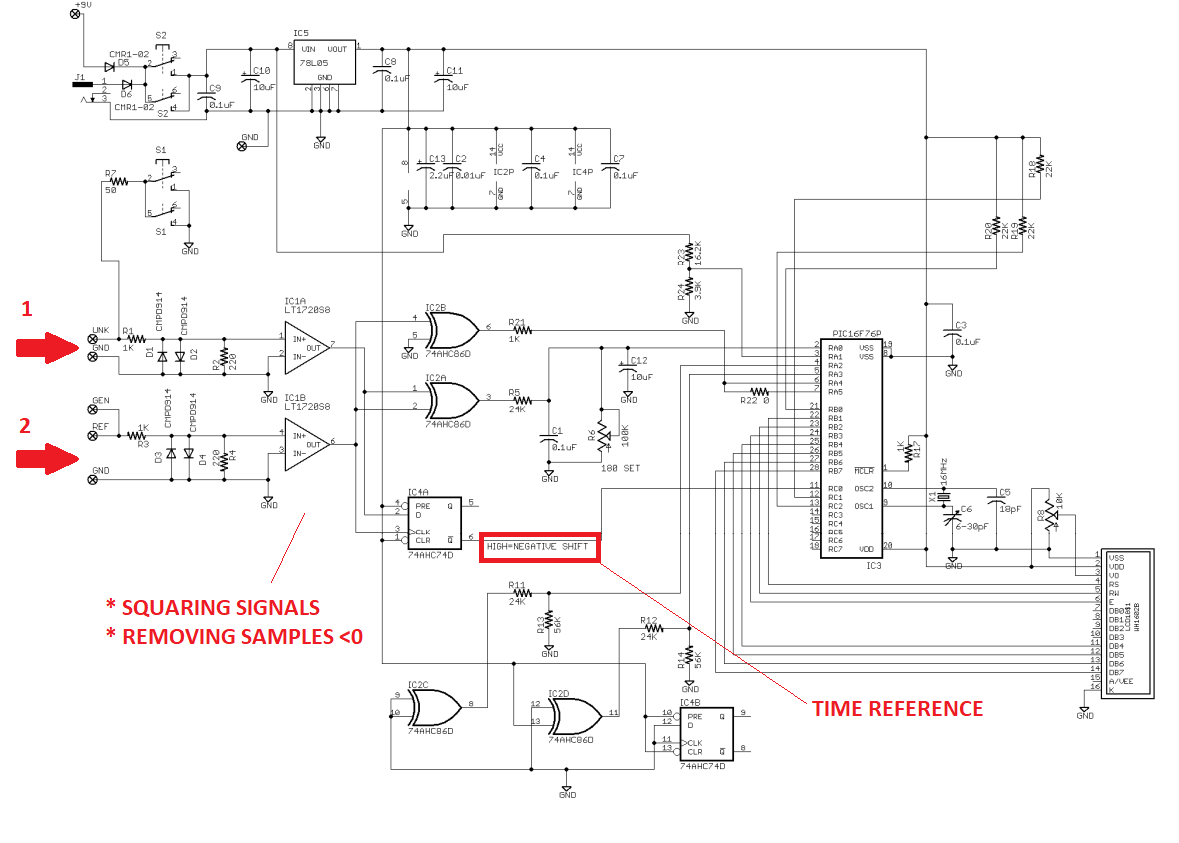
enter image description here

The sign ambiguity is not relevant because one may assume that dph=ph2-ph1 in a certain order, but if the phase difference exceeds 180deg there's again a sign shift in the phase difference.

Therefore the important measurement is the absolute difference between phases.

In the measurement procedure one has to choose what signal is the reference and what signal phase is measured against the eference, thus deciding the order to consider for the difference,

9.- There's room for accuracy improvement

Measuring accuracy repeating for 1e5 rounds

log_err_abs=[]; log_err_rel=[]; num_samples=100000 for k=1:1:num_samples ph1_deg=.1*(2*(randi([1 2],1,1)-1.5))*randi([150 1800],1,1); ph2_deg=.1*(2*(randi([1 2],1,1)-1.5))*randi([150 1800],1,1); ph1=ph1_deg*pi/180; ph2=ph2_deg*pi/180; dph=abs(ph1-ph2); dph_deg=dph*180/pi; x1=sin(2*pi*f1*t+ph1); x2=sin(2*pi*f1*t+ph2); x12=x1.*x2; x5=sign(x1); x6=sign(x2); x56=x5-x6; x56(x56<0)=0; x56=.5*x56; d1_deg=360*numel(x56(x56==0))/numel(x56); if d1_deg>180 d1_deg=360-d1_deg; end % dph_deg; % comparing err_abs=abs(d1_deg-dph_deg); % absolute error err_rel=err_abs/dph_deg*100; % relative error log_err_abs=[log_err_abs err_abs]; log_err_rel=[log_err_rel err_rel]; end figure(8) histogram(log_err_abs,180) grid on title([' Amount samples : ' num2str(num_samples)])

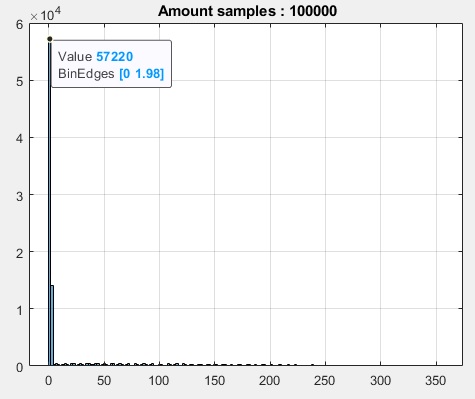
enter image description here

The few scattered large errors are sign inversions that are not considered in the line with clause if d1_deg>360 ..

10.- Regarding amplitude/phase noise, as long as 'small' the floating configuration show in the MFJ222 schematic is a the correct approach for the noise on both branches cancel each other, that never happens, such is the nature of noise, but it get's reduced, it's common practice in RF circuits.

Thanks for reading this answer.

If this answer is found useful would you please conside clicking on the accepted answer.

Improve this answer
$\endgroup$

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.