All, The static stability of the atmosphere is defined as:
$\sigma =-\dfrac{T}{\theta} \dfrac{d\theta}{dp}= \dfrac{dT}{dp}-\dfrac{R}{c_p} \dfrac{T}{p}$
where: $T$ is temperature, $P$ is pressure, $R$ is ideal gas constant, $c_p$ is heat capacity at constant pressure, $\theta$ is potential temperature, which is defined as $\theta=T \left(\dfrac{p_o}{p}\right)^{R/c_p}$, $p_0$ is reference pressure.
The calculated statics stability using $\dfrac{dT}{dp}-\dfrac{R}{c_p} \dfrac{T}{p}$ or $-\dfrac{T}{\theta} \dfrac{d\theta}{dp}$ should be identical, yet they actually differ sometimes as shown below 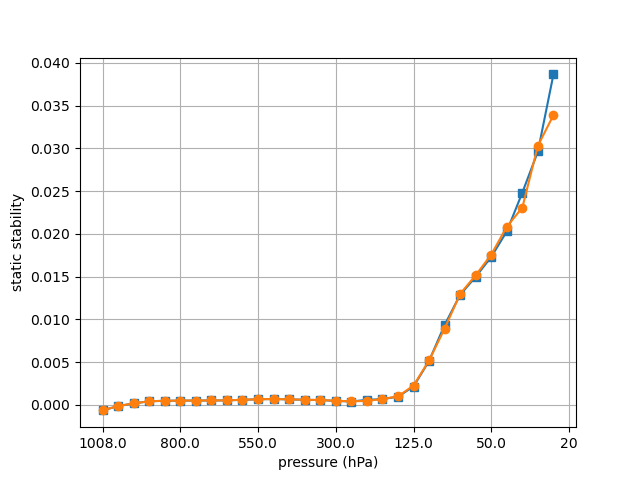
(plz see attached Python code used to calculated statics stability )(plz see attached Python code used to calculated statics stability )
I am wondering if there is analytical or numerical way to determine when both identical definition of static stability might diverge, though? Sometimes, the way that terms is calculated numerically can significantly change the results, for example, the physical properties of the Jacobian of the 2D advection equation was found to differ based on the numerical technique used in the calculation see Arakawa (1966)