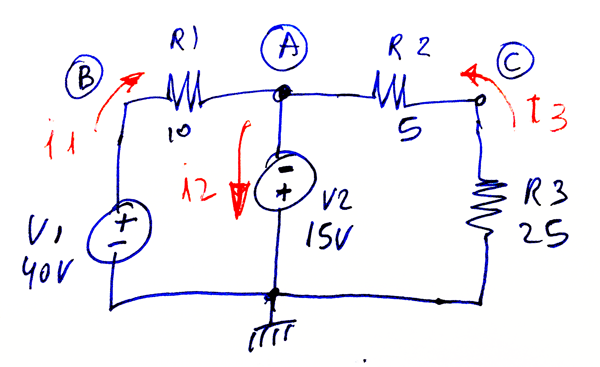
I am trying to do a nodal analysis of this circuit.
and I need to do this by nodal analysis only.
I need to find \$ i_1 \$, \$ i_2 \$ and \$ i_3 \$.
I have found that
\$ i_1 = \frac{V_B - V_A}{R_1} = \frac{40 - (-15)}{10} = \frac{55}{10} = 5.5 A \$
\$ i_3 = \frac{V_A}{R_2 + R_3} = \frac{-15}{5 + 25} = \frac{-15}{30} = -0.5 A \$
Both these value are correct, according to the simulator.
But this is the problem:
\$ i_2 = i_1 + i_3 = 5.5 + (-0.5) = 5 A \$
But the simulator says 6A-6A.
What is the correct way to approach that?