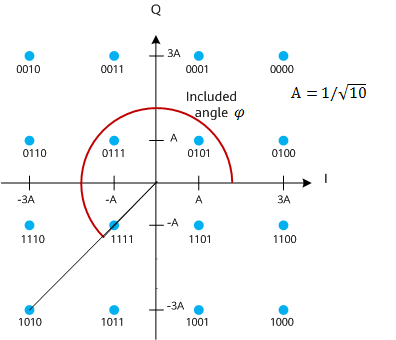
"Stand-Up Maths" recently did a video about QAM/data encoding. He presented a diagram of the encoding spacing for QAM:
I'm from a software engineering background and I couldn't help but think: given that telecommunication companies are always aiming to get more out of the existing infrastructure, why not use a more efficient pattern for a QAM-like encoding scheme?
My original thought was a equilateral triangle spacing:

It satisfies some of the design parameters mentioned in the video (avoiding passing over the origin).
A triangular grid is about 2.3 times denser (the area of a equilateral triangle is about 0.43 with a grid spacing of 1).
My primary question is: what is the limiting factor for such a standard?
- Is it too complex to decode?
- Maybe it doesn't offer any measurable benefit?
- Could it be that a grid follows the same power of 2 expansion rate and that's just easier?
- Perhaps larger encoding spaces can be achieved with increasing the maximum amplitude, rather than a more complex system?
- Backwards compatibility?
- Perhaps there isn't a single bit change "Gray code" system to traverse a triangular graph?
EDIT: After looking at @Attie and @MarcusMüller 's awesome answers AND rewatching the video I have a leading idea that may explain a grid based QAM.
New Question:
If the broadcasted signal is the result of 2 waves constructive and destructive interference and only each waves amplitude is modulated... could it be a Quantization issue?
To clarify I imagine we dont have a broadcasting device that has a perfectly continuous output and therefore can output unlimited resolution for these signals. If that is the case a combination of 2 discrete amplitudes would always result in a grid like pattern.

So a equilateral or irregular symbol distribution would sacrifice a discreet step in order to conform to the non-grid standard. Example created in Desmos: Link
Each purple line represents a discreet amplitude a broadcast device could reliably and accurately achieve.
(The example should show that the purple grid interests at points the equilateral distribution does not, yet the same resolution is required for both schemes.)