2
\$\begingroup\$

I'm trying to calculate the RMS current of a flyback converters primary switch node. The Waveform is shown below:

enter image description here

I'm okay with assuming it is a triangle wave with a duty cycle of 50%. The peak value is 1.25A and the Period time is 4u seconds.

I can calculate it using the following formula I found on the internet:

Text

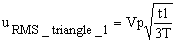
And I will find a RMS current of 0.51A what is right.

But my problem is when I try to calculate it with another method i believe is right I get a different answer. I hope someone can point out me where I'm wrong. See my calculation below:

$$ I_{RMS} = \sqrt{\frac{1}{T}\cdot\int_{0}^{T}I^2(t)dt} $$

I then simplify the integral to an easy area calculation

$$\int_{0}^{T}I^2(t)dt = (0.5 \cdot 0.5T \cdot I_{PK})^2$$

I work this all out to the following:

$$I_{RMS} = \sqrt{\frac{1}{T}(0.5 \cdot 0.5T \cdot I_{PK})^2}$$

When i fill everything in:

$$I_{RMS} = \sqrt{\frac{1}{4\mu}(0.5 \cdot 0.5 \cdot 2\mu \cdot 1.25)^2} $$ $$I_{RMS} = 3.125\cdot10^{-4} A $$

I end up wrong. I think my problem is with the simplification. But it doesn't make sense to me why it should be wrong.

\$\endgroup\$

1 Answer 1

Reset to default
1
\$\begingroup\$

Apply dimensional analysis to see your error. In the third step, you have:

$$ (A) \equiv \sqrt{(s^{-1}) \left[ (A) (s) \right]^2} = \sqrt{ A^2 s} = A \sqrt{ s} $$

which fails the equivalence on the left.

The curve you need to integrate is a quadratic, from 0 to DT, and the remainder (from DT to T) is zero. The antiderivative of the square is 1/3 of the cube, which lies is under the radical, hence where the \$\sqrt{3}\$ fraction comes from.

\$\endgroup\$
1
  • \$\begingroup\$ Thanks for this anwser. I see now where my problem lies. And found my error when simplifying. \$\endgroup\$ Commented May 16, 2023 at 8:25

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.