62
\$\begingroup\$

OK, I already posted this over at math.stackechange.com but didn't get any answers :(

First of here's a picture of my problem, the description follows afterwards:

alt text

So I got all the points and values set up.

The ship starts out moving around the left planet P1 with S=0.27 Degrees per gametick, when it reaches Point A it starts following the bezier curve till it reaches Point D, then it travels around the right planet P2 with S=0.42 Degrees per game tick. The difference in S is so that the travel with the same movement speed around the planets.

So far so good, I got that up and running, now my problem.

When S P1 and S P2 differ to much, the ship jumps between the two speeds when it reaches it's destination, which looks pretty bad. So I need to accelerate the ship between Point A and Point D from S P1 to S P2.

The thing I'm missing are in purple, those are:

  • A way to calculate the ticks it takes the ship to move along the bezier considering the acceleration.

  • And a way to find a position on the bezier curve based on T, again considering the acceleration.

ATM I calculate the length of the bezier by calculating the distance between N of its points. So what I think I need, is a way to scale the T I need to put into my bezier calculation accordingly to the acceleration.

\$\endgroup\$
1
  • 3
    \$\begingroup\$ Good work on figuring that out. I suggest that you post your findings as an answer to your question. \$\endgroup\$ Commented Nov 10, 2010 at 7:40

10 Answers 10

Reset to default
120
\$\begingroup\$

OK, I've got everything working, it took forever, so I'm going to post my detailed solution here.
Note: All code samples are in JavaScript.

So let's break down the problem into the basic parts:

  1. You need to compute the length of, as well as points between 0..1 on the bezier curve

  2. You now need to adjust the scaling of your T to accelerate the ship from one speed to another

Getting the Bezier right

Finding some code for drawing a Bezier curve is easy, there are a number of different approaches though, one of them is the DeCasteljau Algorithm, but you can also just use the equation for cubic Bézier curves: 

// Part of a class, a, b, c, d are the four control points of the curve x: function (t) { return ((1 - t) * (1 - t) * (1 - t)) * this.a.x + 3 * ((1 - t) * (1 - t)) * t * this.b.x + 3 * (1 - t) * (t * t) * this.c.x + (t * t * t) * this.d.x; }, y: function (t) { return ((1 - t) * (1 - t) * (1 - t)) * this.a.y + 3 * ((1 - t) * (1 - t)) * t * this.b.y + 3 * (1 - t) * (t * t) * this.c.y + (t * t * t) * this.d.y; }

With this, one can now draw a bezier curve by calling x and y with t which ranges from 0 to 1, let's take a look:

alt text

Uh... that's not really an even distribution of the points, is it?
Due to the nature of the Bézier curve, the points on 0...1 have different arc lenghts, so segments near the beginning and the end, are longer than the ones which are near to the middle of the curve.

Mapping T evenly on the curve AKA arc-length parameterization

So what to do? Well in simple terms we need a function to map our T onto the t of the curve, so that our T 0.25 results in the t that's at 25% of the length of the curve.

How do we do that? Well, we Google... but it turns out that the term isn't that googleable, and at some point you'll hit this PDF. Which sure is a great read, but in the case that you've already forgotten all the math stuff you learned back in school(or you just don't like those mathematical symbols) it's pretty useless.

What now? Well go and Google some more(read: 6 hours), and you finally find a great article on the topic(including nice pictures! ^_^"):
http://www.planetclegg.com/projects/WarpingTextToSplines.html

Doing the actual code

In case you just couldn't resist downloading that PDF's although you'd already lost your mathematical knowledge a long, long, time ago(and you managed to skip the great article link), you might now think: "God, this will take hundreds of lines of code and tons of CPU"

No, it will not. Because we do what all programmers do, when it comes to math stuff:
We simply cheat.

Arc-length parameterization, the lazy way

Let's face it, we don't need endless precision in our game, do we? So unless you're working at Nasa and planning on sending people the the Mars, you won't need a 0.000001 pixel perfect solution.

So how do we map T onto t? It's simple and only consists of 3 steps:

  1. Calculate N points on the curve using t and store the arc-length(aka the length of the curve) at that position into an array

  2. To map T onto t, first multiply T by the total length of the curve to get u and then search the array of lengths for the index of the largest value that's smaller than u

  3. If we had an exact hit, return the array value at that index divided by N, if not interpolate a bit between the point we found and the next one, divide the thing once again by N and return.

That's all! So now let's take a look at the complete code: 

function Bezier(a, b, c, d) { this.a = a; this.b = b; this.c = c; this.d = d; this.len = 100; this.arcLengths = new Array(this.len + 1); this.arcLengths[0] = 0; var ox = this.x(0), oy = this.y(0), clen = 0; for(var i = 1; i <= this.len; i += 1) { var x = this.x(i * 0.05), y = this.y(i * 0.05); var dx = ox - x, dy = oy - y; clen += Math.sqrt(dx * dx + dy * dy); this.arcLengths[i] = clen; ox = x, oy = y; } this.length = clen; }

This initializes our new curve and computes the arg-lenghts, it also stores the last of the lengths as the total length of the curve, key factor here is this.len which is our N. The higher, the more precise the mapping will be, for a curve of the size in the picture above 100 points seem to be enough, if you just need a good length estimate, something like 25 will already do the job with being only 1 pixel off in our example, but then you will have a less precise mapping which will result in not so even distribution of T when mapped to t.

Bezier.prototype = { map: function(u) { var targetLength = u * this.arcLengths[this.len]; var low = 0, high = this.len, index = 0; while (low < high) { index = low + (((high - low) / 2) | 0); if (this.arcLengths[index] < targetLength) { low = index + 1; } else { high = index; } } if (this.arcLengths[index] > targetLength) { index--; } var lengthBefore = this.arcLengths[index]; if (lengthBefore === targetLength) { return index / this.len; } else { return (index + (targetLength - lengthBefore) / (this.arcLengths[index + 1] - lengthBefore)) / this.len; } }, mx: function (u) { return this.x(this.map(u)); }, my: function (u) { return this.y(this.map(u)); },

The actual mapping code, first we do a simple binary search on our stored lengths to find the largest length that's smaller then targetLength, then we just return or do the interpolation and return.

 x: function (t) { return ((1 - t) * (1 - t) * (1 - t)) * this.a.x + 3 * ((1 - t) * (1 - t)) * t * this.b.x + 3 * (1 - t) * (t * t) * this.c.x + (t * t * t) * this.d.x; }, y: function (t) { return ((1 - t) * (1 - t) * (1 - t)) * this.a.y + 3 * ((1 - t) * (1 - t)) * t * this.b.y + 3 * (1 - t) * (t * t) * this.c.y + (t * t * t) * this.d.y; } };

Again this computes t on the curve.

Time for results

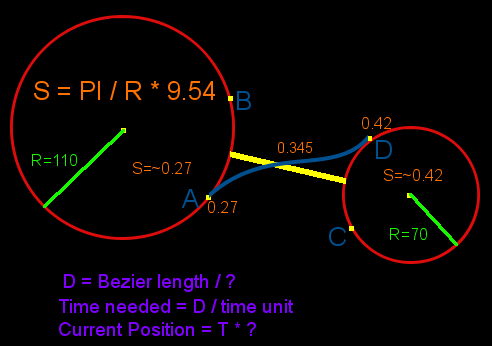
alt text

By now using mx and my you get an evenly distributed T on the curve :)

Wasn't that hard, was it? Once again, it turns out that a simple(although not perfect solution) will be enough for a game.

In case you want to see the complete code, there's a Gist available:
https://gist.github.com/670236

Finally, accelerating the ships

So all that's left now is to accelerate the ships along their path, by mapping the position onto T which we then use to find the t on our curve.

First we need two of the equations of motion, namely ut + 1/2at² and (v - u) / t

In actual code that would look like this: 

startSpeed = getStartingSpeedInPixels() // Note: pixels endSpeed = getFinalSpeedInPixels() // Note: pixels acceleration = (endSpeed - startSpeed) // since we scale to 0...1 we can leave out the division by 1 here position = 0.5 * acceleration * t * t + startSpeed * t;

Then we scale that down to 0...1 by doing: 

maxPosition = 0.5 * acceleration + startSpeed; newT = 1 / maxPosition * position;

And there you go, the ships are now moving smoothly along the path.

In case it doesn't work...

When you're reading this, everything works fine and dandy, but I initially had some problems with the acceleration part, when explaining the problem to someone in the gamedev chatroom I found the final error in my thinking.

In case you haven't forgotten already about the picture in the original question, I mention s there, turns out that s is speed in degrees, but the ships move along the path in pixels and I had forgotten about that fact. So what I needed to do in this case was to convert the displacement in degrees into a displacement in pixels, turns out that this is rather easy: 

function rotationToMovement(planetSize, rotationSpeed) { var r = shipAngle * Math.PI / 180; var rr = (shipAngle + rotationSpeed) * Math.PI / 180; var orbit = planetSize + shipOrbit; var dx = Math.cos(r) * orbit - Math.cos(rr) * orbit; var dy = Math.sin(r) * orbit - Math.sin(rr) * orbit; return Math.sqrt(dx * dx + dy * dy); };

So and that's all! Thanks for reading ;)

\$\endgroup\$
10
  • 7
    \$\begingroup\$ This is going to take a while to digest. But wow, amazing answer to your own question. \$\endgroup\$ Commented Nov 11, 2010 at 17:59
  • 11
    \$\begingroup\$ I made an account just to upvote this answer \$\endgroup\$ Commented Jan 26, 2011 at 12:09
  • 4
    \$\begingroup\$ 'i' is multiplied by 0.05, while 'len' was set to 100. this would 't' to be mapped to '0-5' instead of '0-1'. \$\endgroup\$ Commented Jun 5, 2014 at 14:30
  • 3
    \$\begingroup\$ @EvilActivity Yeah I saw that too, his original length must have been 20, then forgot to change 0.05 to 0.01. So better have a dynamic 'len' (adaptive to the true arc length, or maybe even exactly equal to it), and calculate the "step" by 1/'len'. I find it so weird noone else has brought this up all these years!!! \$\endgroup\$ Commented Jan 6, 2015 at 13:58
  • 1
    \$\begingroup\$ The accepted answer mentions a PDF document "Moving Along a Curve with Specified Speed" by D. Eberly and then dismisses it, proposing an interpolation-based solution. But to be fair, this is exactly what Section 6 of that document is about ("Avoiding the Numerical Solution at Runtime"). \$\endgroup\$ Commented Apr 7, 2020 at 3:07
7
\$\begingroup\$

The issue is that a ship would not take that trajectory naturally. So even with it working perfectly it still won't look right.

If you want to simulate the smooth transition between planets I would suggest actually modeling it. The equations are very simple as you only have two significant forces: gravity, and thrust.

You just need to set your constants: Mass of P1, P2, ship

With each game-tick (time: t) you are doing 3 things

  1. Calculate the gravity of p1 on ship and p2 on ship, add the resultant vectors to the thrust vector.

  2. Calculate your new velocity based on your new acceleration from step 1

  3. Move the ship according to your new velocity

Might seem like a lot of work but it can be done in a dozen lines of code and will look very natural.

If you need help with the physics let me know.

\$\endgroup\$
2
  • \$\begingroup\$ I might consider testing that if you can provide a way of doing this within a function that takes t :) \$\endgroup\$ Commented Nov 11, 2010 at 16:37
  • 1
    \$\begingroup\$ -but in game programming you don't use t as a variable. You're already basically in a parametric situation, because you're simply calculating the new dx and dy for the ship. Here's an example of orbiting two planets (in Flash) aharrisbooks.net/flash/fg2r12/twoPlanets.html - and here's the same thing in Python: aharrisbooks.net/pythonGame/ch09/twoPlanets.py \$\endgroup\$ Commented Nov 13, 2010 at 3:09
3
\$\begingroup\$

This problem is just begging for Newton approximation like recursions.

How to find distance of arc up to precision required?

First iteration: Find out the distance between both endpoints. Create new points at 1/4 of a distance from 1/4 first control point to 3/4 of second control point, plus 3/4 of a distance from 1st point, plus 1/2 the distance. Measure length of a polyline comprising these five points. Is second distance minus first distance smaller than our tolerance?

  • yes => return distance
  • no => recursion Other iterations: Create points at 1/8, 3/8, 5/8 and 7/8 (or 1/16th, 3/16ths etc., and so on in subsequent iterations) Is new distance - previous distance < tolerance? Yes/no, return distance/recursion.

In this way not only can you tell what the distance is, but also what is maximum imprecision in your calculation, plus you never calculate more than what is absolutely necessary.

To find the point at t I would strongly suggest using pure Newton's approximation, as this is what it calculates, and within defined toleration.

Pyhon code, created and tested in Blender 2.83 LTS.

from math import sqrt def lengthOfCurve(points, H1, H2, toleration): A = points[0] E = points[-1] if len(points) == 2: # first round Ba = [(H1[0] - A[0])*0.25 + A[0], (H1[1] - A[1])*0.25 + A[1], (H1[2] - A[2])*0.25 + A[2]] Bb = [(E[0] - H2[0])*0.25 + H2[0], (E[1] - H2[1])*0.25 + H2[1], (E[2] - H2[2])*0.25 + H2[2]] B = [(Bb[0] - Ba[0])*0.25 + Ba[0], (Bb[1] - Ba[1])*0.25 + Ba[1], (Bb[2] - Ba[2])*0.25 + Ba[2]] Ca = [(H1[0] - A[0])*0.5 + A[0], (H1[1] - A[1])*0.5 + A[1], (H1[2] - A[2])*0.5 + A[2]] Cb = [(E[0] - H2[0])*0.5 + H2[0], (E[1] - H2[1])*0.5 + H2[1], (E[2] - H2[2])*0.5 + H2[2]] C = [(Cb[0] - Ca[0])*0.5 + Ca[0], (Cb[1] - Ca[1])*0.5 + Ca[1], (Cb[2] - Ca[2])*0.5 + Ca[2]] Da = [(H1[0] - A[0])*0.75 + A[0], (H1[1] - A[1])*0.75 + A[1], (H1[2] - A[2])*0.75 + A[2]] Db = [(E[0] - H2[0])*0.75 + H2[0], (E[1] - H2[1])*0.75 + H2[1], (E[2] - H2[2])*0.75 + H2[2]] D = [(Db[0] - Da[0])*0.75 + Da[0], (Db[1] - Da[1])*0.75 + Da[1], (Db[2] - Da[2])*0.75 + Da[2]] points = [A, B, C, D, E] originalLength = sizeOfVector(A, E) newLength = sizeOfVector(A, B) + sizeOfVector(B, C) + sizeOfVector(C, D) + sizeOfVector(D, E) if newLength - toleration < originalLength: return(round(newLength/toleration)*toleration) return(lengthOfCurve(points, H1, H2, toleration)) else: # following rounds numberOfSegments = len(points) - 1 points2 = [] i = numberOfSegments while i > 0: t = 2*i - 1 pointA = [(H1[0] - A[0])*(t/(2*numberOfSegments)) + A[0], (H1[1] - A[1])*(t/(2*numberOfSegments)) + A[1], (H1[2] - A[2])*(t/(2*numberOfSegments)) + A[2]] pointB = [(E[0] - H2[0])*(t/(2*numberOfSegments)) + H2[0], (E[1] - H2[1])*(t/(2*numberOfSegments)) + H2[1], (E[2] - H2[2])*(t/(2*numberOfSegments)) + H2[2]] point = [(pointB[0] - pointA[0])*(t/(2*numberOfSegments)) + pointA[0], (pointB[1] - pointA[1])*(t/(2*numberOfSegments)) + pointA[1], (pointB[2] - pointA[2])*(t/(2*numberOfSegments)) + pointA[2]] points2.insert(0, point) # I am prepending, because I am advancing bacwards i -= 1 newPoints = [] i = 0 while i < numberOfSegments: # join points and points2 using zipper newPoints.append(points[i]) newPoints.append(points2[i]) i += 1 newPoints.append(points[numberOfSegments]) newLength = 0 i = numberOfSegments while i > 0: newLength += sizeOfVector(newPoints[2*i], newPoints[2*i - 1]) newLength += sizeOfVector(newPoints[2*i - 1], newPoints[2*i - 2]) i -= 1 originalLength = 0 i = int(numberOfSegments/2) while i > 0: originalLength += sizeOfVector(points[2*i], points[2*i - 1]) originalLength += sizeOfVector(points[2*i - 1], points[2*i - 2]) i -= 1 if newLength - toleration < originalLength: return(round(newLength/toleration)*toleration) return(lengthOfCurve(newPoints, H1, H2, toleration)) def sizeOfVector(P, Q): return(sqrt((P[0] - Q[0])*(P[0] - Q[0]) + (P[1] - Q[1])*(P[1] - Q[1]) + (P[2] - Q[2])*(P[2] - Q[2]))) point1 = [0, 0, 0] point2 = [1, 0, 0] handle1 = [0, 1, 0] handle2 = [1, 1, 0] toleration = 0.01 print(lengthOfCurve([point1, point2], handle1, handle2, toleration))

EDIT: Ok, I got the t working as well, within toleration, as expected. It was far from simple approximation. Let me know if there is dire need for it in English. I did all of this in a single day and I feel a bit exhausted to translate the second chunk from Czech at the moment.

2nd day edit 2: Fixed precision inaccuracy, made as foolproof as possible, translated into EN

from math import sqrt def lengthOfCurve(points, H1, H2, toleration): A = points[0] E = points[-1] if len(points) == 2: # round one Ba = [(H1[0] - A[0])*0.25 + A[0], (H1[1] - A[1])*0.25 + A[1], (H1[2] - A[2])*0.25 + A[2]] Bb = [(E[0] - H2[0])*0.25 + H2[0], (E[1] - H2[1])*0.25 + H2[1], (E[2] - H2[2])*0.25 + H2[2]] B = [(Bb[0] - Ba[0])*0.25 + Ba[0], (Bb[1] - Ba[1])*0.25 + Ba[1], (Bb[2] - Ba[2])*0.25 + Ba[2]] Ca = [(H1[0] - A[0])*0.5 + A[0], (H1[1] - A[1])*0.5 + A[1], (H1[2] - A[2])*0.5 + A[2]] Cb = [(E[0] - H2[0])*0.5 + H2[0], (E[1] - H2[1])*0.5 + H2[1], (E[2] - H2[2])*0.5 + H2[2]] C = [(Cb[0] - Ca[0])*0.5 + Ca[0], (Cb[1] - Ca[1])*0.5 + Ca[1], (Cb[2] - Ca[2])*0.5 + Ca[2]] Da = [(H1[0] - A[0])*0.75 + A[0], (H1[1] - A[1])*0.75 + A[1], (H1[2] - A[2])*0.75 + A[2]] Db = [(E[0] - H2[0])*0.75 + H2[0], (E[1] - H2[1])*0.75 + H2[1], (E[2] - H2[2])*0.75 + H2[2]] D = [(Db[0] - Da[0])*0.75 + Da[0], (Db[1] - Da[1])*0.75 + Da[1], (Db[2] - Da[2])*0.75 + Da[2]] points = [A, B, C, D, E] originalLength = lengthOfVector(A, E) newLength = lengthOfVector(A, B) + lengthOfVector(B, C) + lengthOfVector(C, D) + lengthOfVector(D, E) if newLength - toleration < originalLength: return(round(newLength/toleration)*toleration) return(lengthOfCurve(points, H1, H2, toleration)) else: # following rounds numberOfSegments = len(points) - 1 points2 = [] i = numberOfSegments while i > 0: t = 2*i - 1 pointA = [(H1[0] - A[0])*(t/(2*numberOfSegments)) + A[0], (H1[1] - A[1])*(t/(2*numberOfSegments)) + A[1], (H1[2] - A[2])*(t/(2*numberOfSegments)) + A[2]] pointB = [(E[0] - H2[0])*(t/(2*numberOfSegments)) + H2[0], (E[1] - H2[1])*(t/(2*numberOfSegments)) + H2[1], (E[2] - H2[2])*(t/(2*numberOfSegments)) + H2[2]] point = [(pointB[0] - pointA[0])*(t/(2*numberOfSegments)) + pointA[0], (pointB[1] - pointA[1])*(t/(2*numberOfSegments)) + pointA[1], (pointB[2] - pointA[2])*(t/(2*numberOfSegments)) + pointA[2]] points2.insert(0, point) # i am prepending because I advance back first i -= 1 newPoints = [] i = 0 while i < numberOfSegments: # join points and points2 using zipper method newPoints.append(points[i]) newPoints.append(points2[i]) i += 1 newPoints.append(points[numberOfSegments]) newLength = 0 i = numberOfSegments while i > 0: newLength += lengthOfVector(newPoints[2*i], newPoints[2*i - 1]) newLength += lengthOfVector(newPoints[2*i - 1], newPoints[2*i - 2]) i -= 1 originalLength = 0 i = int(numberOfSegments/2) while i > 0: originalLength += lengthOfVector(points[2*i], points[2*i - 1]) originalLength += lengthOfVector(points[2*i - 1], points[2*i - 2]) i -= 1 if newLength - toleration < originalLength: return(round(newLength/toleration)*toleration) return(lengthOfCurve(newPoints, H1, H2, toleration)) def lengthOfVector(P, Q): return(sqrt((P[0] - Q[0])*(P[0] - Q[0]) + (P[1] - Q[1])*(P[1] - Q[1]) + (P[2] - Q[2])*(P[2] - Q[2]))) point1 = [0, 0, 0] point2 = [1, 0, 0] handle1 = [0, 1, 0] handle2 = [1, 1, 0] toleration = 0.01 print("length of curve = ", lengthOfCurve([point1, point2], handle1, handle2, toleration)) def findPoints(points, H1, H2, toleration, lengthOfCurv): A = points[0] E = points[-1] if len(points) == 2: # round one Ba = [(H1[0] - A[0])*0.25 + A[0], (H1[1] - A[1])*0.25 + A[1], (H1[2] - A[2])*0.25 + A[2]] Bb = [(E[0] - H2[0])*0.25 + H2[0], (E[1] - H2[1])*0.25 + H2[1], (E[2] - H2[2])*0.25 + H2[2]] B = [(Bb[0] - Ba[0])*0.25 + Ba[0], (Bb[1] - Ba[1])*0.25 + Ba[1], (Bb[2] - Ba[2])*0.25 + Ba[2]] Ca = [(H1[0] - A[0])*0.5 + A[0], (H1[1] - A[1])*0.5 + A[1], (H1[2] - A[2])*0.5 + A[2]] Cb = [(E[0] - H2[0])*0.5 + H2[0], (E[1] - H2[1])*0.5 + H2[1], (E[2] - H2[2])*0.5 + H2[2]] C = [(Cb[0] - Ca[0])*0.5 + Ca[0], (Cb[1] - Ca[1])*0.5 + Ca[1], (Cb[2] - Ca[2])*0.5 + Ca[2]] Da = [(H1[0] - A[0])*0.75 + A[0], (H1[1] - A[1])*0.75 + A[1], (H1[2] - A[2])*0.75 + A[2]] Db = [(E[0] - H2[0])*0.75 + H2[0], (E[1] - H2[1])*0.75 + H2[1], (E[2] - H2[2])*0.75 + H2[2]] D = [(Db[0] - Da[0])*0.75 + Da[0], (Db[1] - Da[1])*0.75 + Da[1], (Db[2] - Da[2])*0.75 + Da[2]] points = [A, B, C, D, E] longestSegment = lengthOfVector(A, B) lenBC = lengthOfVector(B, C) lenCD = lengthOfVector(C, D) lenDE = lengthOfVector(D, E) if lenBC > longestSegment: longestSegment = lenBC if lenCD > longestSegment: longestSegment = lenBC if lenDE > longestSegment: longestSegment = lenBC if longestSegment < toleration: return(points) return(findPoints(points, H1, H2, toleration, lengthOfCurv)) else: # following rounds numberOfSegments = len(points) - 1 points2 = [] i = numberOfSegments while i > 0: t = 2*i - 1 pointA = [(H1[0] - A[0])*(t/(2*numberOfSegments)) + A[0], (H1[1] - A[1])*(t/(2*numberOfSegments)) + A[1], (H1[2] - A[2])*(t/(2*numberOfSegments)) + A[2]] pointB = [(E[0] - H2[0])*(t/(2*numberOfSegments)) + H2[0], (E[1] - H2[1])*(t/(2*numberOfSegments)) + H2[1], (E[2] - H2[2])*(t/(2*numberOfSegments)) + H2[2]] point = [(pointB[0] - pointA[0])*(t/(2*numberOfSegments)) + pointA[0], (pointB[1] - pointA[1])*(t/(2*numberOfSegments)) + pointA[1], (pointB[2] - pointA[2])*(t/(2*numberOfSegments)) + pointA[2]] points2.insert(0, point) # i am prepending because I advance back first i -= 1 newPoints = [] i = 0 while i < numberOfSegments: # join points and points2 using zipper method newPoints.append(points[i]) newPoints.append(points2[i]) i += 1 newPoints.append(points[numberOfSegments]) newLength = 0 i = numberOfSegments while i > 0: newLength += lengthOfVector(newPoints[2*i], newPoints[2*i - 1]) newLength += lengthOfVector(newPoints[2*i - 1], newPoints[2*i - 2]) i -= 1 originalLength = 0 i = int(numberOfSegments/2) longestSegment = 0 while i > 0: byHowMuch = lengthOfVector(points[2*i], points[2*i - 1]) if byHowMuch > longestSegment: longestSegment = byHowMuch originalLength += byHowMuch byHowMuch = lengthOfVector(points[2*i - 1], points[2*i - 2]) if byHowMuch > longestSegment: longestSegment = byHowMuch originalLength += byHowMuch i -= 1 #print(longestSegment) if longestSegment < toleration: return(newPoints) return(findPoints(newPoints, H1, H2, toleration, lengthOfCurv)) def pointOnCurve(point1, point2, handle1, handle2, placement, toleration, lengthOfCurv): aggregateLength = lengthOfCurve([point1, point2], handle1, handle2, toleration) lengthOfUnfinishedCurve = aggregateLength*placement sequence = findPoints([point1, point2], handle1, handle2, toleration, lengthOfCurv) aggregateLength = 0 for i, s in enumerate(sequence): aggregateLength += lengthOfVector([sequence[i][0], sequence[i][1], sequence[i][2]], [sequence[i + 1][0], sequence[i + 1][1], sequence[i + 1][2]]) if aggregateLength >= lengthOfUnfinishedCurve: return([round(sequence[i + 1][0]/toleration)*toleration, round(sequence[i + 1][1]/toleration)*toleration, round(sequence[i + 1][2]/toleration)*toleration]) point1 = [0, 0, 0] point2 = [1, 0, 0] handle1 = [0, 1, 0] handle2 = [1, 1, 0] toleration = 0.01 placement = 0.3 lengthOfCurv = lengthOfCurve([point1, point2], handle1, handle2, toleration) print("point on curve = ", pointOnCurve(point1, point2, handle1, handle2, placement, toleration, lengthOfCurv))
\$\endgroup\$
2
\$\begingroup\$

I found an excellent article explaining a possible solution to this problem with a code example written in javascript. It works by "nudging the t" value into the right direction.

Instead, we can use the fact that the average leg length d_avg for any dot distribution is nearly identical to the leg lengths that evenly-spaced dots would produce (this similarity increases as n increases). If we calculate the difference d_err between the actual leg lengths d and the average leg length d_avg, then the time parameter t corresponding to each point can be nudged to reduce this difference.

This question has already a lot of cool answers, but i found this solution to be worth noticing.

\$\endgroup\$
1
  • \$\begingroup\$ The link seems to be kind of dead? \$\endgroup\$ Commented May 20 at 13:34
1
\$\begingroup\$

Thanks for your excellent page describing how you solved this problem. I did something somewhat different than you in one detail, as I was deeply memory constrained: I don't build an array, or have to search it for the right 'segment' with a binary search. This is because I always know I am moving from one end of my Bezier curve to another: Therefore, I simply remember the 'current' segment, and if I see that I am going to go out of bounds of that segment to compute my next position, I compute the next (or previous) segment (based on direction of travel.) This works quite well for my application. The only glitch I had to work out was that, in some curves, the size of the segments were so small that my next plot to point was - at rare times - more than one segment ahead of the current one, so instead of just going to the 'next' or 'previous' segment (based on direction), I had to compute segments forward (or back) until I found the one that my next point was 'in'.

Don't know if this quite makes sense, but this certainly helped me.

\$\endgroup\$
1
\$\begingroup\$

The problem with the accepted solution

As Bezier an exponential function, we expect different rates of advance in different areas of the curve.

Because Ivo's solution linearly interpolates between these initial exponential samples, inaccuracies will be heavily biased towards ends / middle of the (typically cubic) curve where those deltas are greatest; so unless the sample rate N is increased greatly as he suggests, errors are apparent, and at some level of zoom, will always be apparent for a given N, i.e. the bias is intrinsic for that algorithm. Not good for e.g. vector-based graphics where zoom may be unlimited.

Countering bias through guided sampling

An alternative solution is to linearly remap distance to t after countering the natural bias that the Bezier function produces.

Assuming this is what we ideally want:

curve length = 10 t distance 0.2 2 0.4 4 0.6 6 0.8 8 1.0 10

but this is what we get from the Bezier position function:

t distance 0.2 0.12 0.4 1.22 0.6 2.45 0.8 5.81 1.0 10.00

By looking at N samples taken, we can see where distance deltas are greatest, and resample ("split") midway between the two adjacent distances, increasing N by 1. For example, splitting at t=0.9 (which is midway in the largest delta), we might get:

0.8 5.81 0.9 7.39 1.0 10.00

We repeat this process for the next largest distance interval until the maximum delta between any two distances in the entire set is below some minDistanceDelta, and more specifically, less than epsilon away from specific distances we want to map to steps of t; we can then linearly map our desired t steps to corresponding distances. This produces a hashtable / map which you can cheaply access and whose values you can lerp between, at runtime, without bias.

As the set grows in N, the cost to repeat this increases, so ideally do this as a pre-process. Each time N increases, add the two new resultant intervals to an intervals collection while removing the old, single interval they replaced. This is the structure on which you work to find the next greatest interval to split into two. Keeping intervals sorted by distance keeps things easy, as you can just pop next work item off the end, and split etc.

We end up with something like what we ideally wanted:

epsilon: 0.01 t distance 0.200417 2.00417 0.3998132 3.9998132 0.600703 6.00703 0.800001 8.00001 0.9995309 9.995309

Since we are taking guesses at every step, we will not get exact the exact distances 2, 4 etc. we wanted, but through repeat iteration these get close enough to the desired distance values so you can map to your t steps with fair accuracy, eliminating bias due to near-equidistant sampling.

You can then retrieve e.g. t=0.5, as Ivo does in his answer, i.e. by interpolating between the two nearest values above (3.9998132 and 6.00703).

Conclusion

For most cases, Ivo's solution will work well, but for cases where bias must be avoided at all costs, be sure that your distances are as evenly scattered as possible, and then linearly mapped to t.

Note that splitting could be done stochastically rather than splitting down the middle each time, for example we might have split that first example interval at t=0.827 rather than at t=0.9.

\$\endgroup\$
0
\$\begingroup\$

That kind of modeling is strange, and can produce weird illogical results. Especially if the starting planets speed is really slow.

Model the ships with a thrust power.

When the ships are on their last orbit on the starting planet, accelerate with full thrust.

When the ship gets within a certain distance use reverse thrust to slow the ship down to the target planet's orbit speed.

Edit: Do the entire simulation at once when a node is about to leave the orbit. either send all the data, or send just a few of movement vectors at intervals, and interpolate between them.

\$\endgroup\$
2
  • \$\begingroup\$ Problem is, this is all tick based, there's no intermediate position. It's a networking multiplayer game and sending all the positions of 600+ ships in a full game will kill all networking. There are only events which transmit a tickOffset, the rest is calculated based on the current world tick and the offset. \$\endgroup\$ Commented Nov 9, 2010 at 20:30
  • \$\begingroup\$ I edited my response. \$\endgroup\$ Commented Nov 9, 2010 at 21:14
0
\$\begingroup\$

If I understand it correctly, your problem is over-constrained.

I believe that you want the spaceship to travel along a specified path between orbits in some time t, and you also want it to accelerate from speed s1 to speed s2 in the same time t. Unfortunately, you can't (in general) find an acceleration that satisfies both of these constraints simultaneously.

You're going to have to relax your problem a bit to make it solvable.

\$\endgroup\$
3
  • 2
    \$\begingroup\$ Then how to relax it? What I could imagine is modifying the T that I plug into the bezier path stuff. I would need to scale it somehow to first grow slower to 0.5 and then faster to 1. So the ship decelerates from it's original speed to a fixed one at the middle of the curve and then accelerates again from this speed to the speed at the end of the curve? \$\endgroup\$ Commented Nov 9, 2010 at 22:22
  • 1
    \$\begingroup\$ I think it will look more realistic if the spaceship accelerates from its original speed to somewhere around the midpoint of the transfer and then decelerates to the new orbit. \$\endgroup\$ Commented Nov 9, 2010 at 22:32
  • \$\begingroup\$ Still I'm stuck on how to plug the acceleration into the whole thing, I need to modify the T somehow :/ \$\endgroup\$ Commented Nov 9, 2010 at 23:40
0
\$\begingroup\$

I came across this answer because I'm looking to distribute points evenly along an svg path that uses a bezier curve.

Despite MDN saying it's deprecated, you can use the path.getPointAtLength to get the correct result. https://developer.mozilla.org/en-US/docs/Web/API/SVGPathElement/getPointAtLength

It currently works in Chrome/Safari/Firefox, and should work in IE/Edge as well but I didn't verify those 2.

\$\endgroup\$
0
\$\begingroup\$

This thread helped me with my solution. So I'll share the code:

 public static List<Vector3> BezierCurvePoints(Vector3 p0, Vector3 p1, Vector3 p2, Vector3 p3, int pointCount = 30) { var rawPoints = new List<Vector3>(); length = 0.0f; Vector3 lastPoint = BezierPoint(0, p0, p1, p2, p3); rawPoints.Add(p0); for (int i = 1; i <= pointCount; i++) { var point = BezierPoint((float)i / (float)pointCount, p0, p1, p2, p3); length += Vector3.Distance(point, lastPoint); lastPoint = point; rawPoints.Add(point); } rawPoints.Add(p3); var adjustedPoints = new List<Vector3>(); adjustedPoints.Add(p0); float segmentLength = length / (pointCount-1); // Because X points translates into X-1 segments float forNextAdjustedSegment = segmentLength; int rawIndex = 1; bool rawSegmentValid = false; float rawSegmentLength = 0; Vector3 rawPointA = Vector3.zero; Vector3 rawPointB = Vector3.zero; while (adjustedPoints.Count < pointCount-1) { if (!rawSegmentValid) { rawPointA = rawPoints[rawIndex - 1]; rawPointB = rawPoints[rawIndex]; rawSegmentLength = Vector3.Distance(rawPointA, rawPointB); } if (rawSegmentLength >= forNextAdjustedSegment) { adjustedPoints.Add(Vector3.Lerp(rawPointA, rawPointB, forNextAdjustedSegment / rawSegmentLength)); forNextAdjustedSegment += segmentLength; } else { forNextAdjustedSegment -= rawSegmentLength; rawSegmentValid = false; rawIndex++; if (rawIndex >= rawPoints.Count) { Debug.LogError("Outside of Raw Indexes. Breaking"); break; } } } adjustedPoints.Add(p3); return adjustedPoints; }

The forNextAdjustedSegment may be confusing. The idea is that we are slowly moving from point to point, but keep track of lengths.

To get a position:

 public Vector3 GetPoint(float portion, Vector3 start, Vector3 end) { float pointSection = Mathf.Clamp01(portion) * (points.Count-1); var from = points[Mathf.FloorToInt(pointSection)]; var to = points[Mathf.CeilToInt(pointSection - float.Epsilon * 10)]; return Vector3.Lerp(from, to, pointSection % 1); }
\$\endgroup\$

You must log in to answer this question.

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.