By Flanigan & Kazdan: 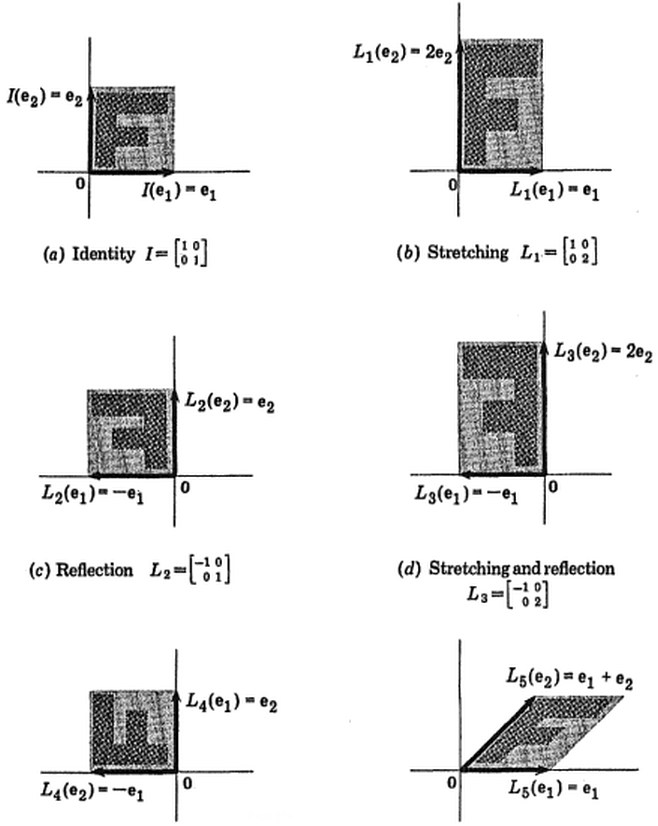

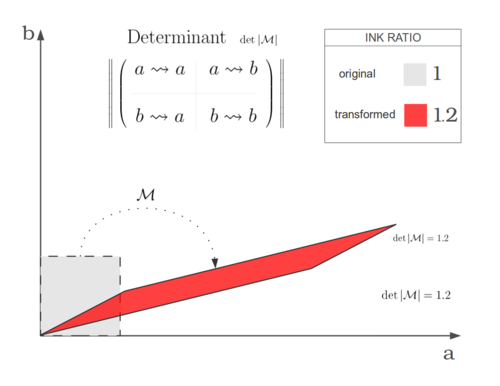
Instead of looking at a "box of numbers", look at the "total action" after applying the whole thing. It's an automorphism of linear spaces, meaning that in some vector-linear-algebra-type situation this is "turning things over and over in your hands without breaking the algebra that makes it be what it is". (Modulo some things—like maybe you want a constant determinant.)
This is also why order matters: if you compose the matrices in one direction it might not be the same as the other. $$^1_4 \Box ^2_3 {} \xrightarrow{\mathbf{V} \updownarrow} {} ^4_1 \Box ^3_2 {} \xrightarrow{\Theta_{90} \curvearrowright} {} ^1_2 \Box ^4_3 $$ versus $$^1_4 \Box ^2_3 {} \xrightarrow{\Theta_{90} \curvearrowright} {} ^4_3 \Box ^1_2 {} \xrightarrow{\mathbf{V} \updownarrow} {} ^3_4 \Box ^2_1 $$
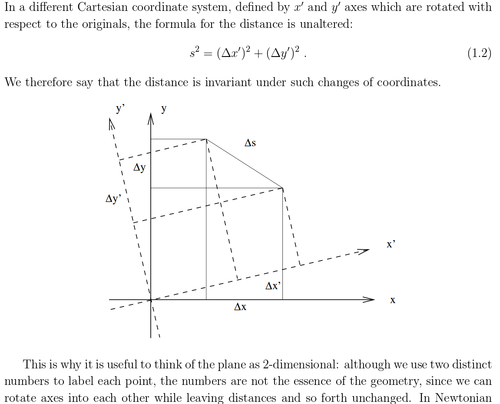
The actions can be composed (one after the other)—that's what multiplying matrices does. Eventually the matrix representing the overall cumulative effect of whatever things you composed, should be applied to something. For this you can say "the plane", or pick a few points, or draw an F, or use a real picture (computers are good at linear transformations after all).
 the 3-D version http://www.kidsmathgamesonline.com/images/pictures/shapes/parallelepiped.jpg
the 3-D version http://www.kidsmathgamesonline.com/images/pictures/shapes/parallelepiped.jpg
You could also watch the matrices work on Mona step by step too, to help your intuition.
Finally I think you can think of matrices as "multidimensional multiplication". $$y=mx+b$$ is affine; the truly "linear" (keeping $0 \overset{f}{\longmapsto} 0$) would be less complicated: just $$y=mx$$ (eg.  ) which is an "even"
) which is an "even" 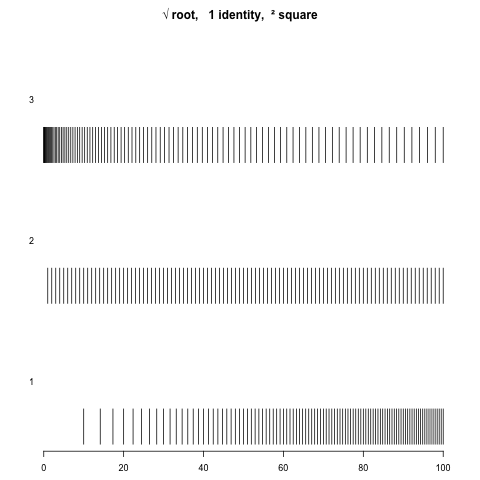 stretching/dilation. $$\vec{y}=\left[ \mathbf{M} \right] \vec{x}$$ really is the multi-dimensional version of the same thing, it's just that when you have multiple numbers in each $\vec{x}$ each of the dimensions can impinge on each other
stretching/dilation. $$\vec{y}=\left[ \mathbf{M} \right] \vec{x}$$ really is the multi-dimensional version of the same thing, it's just that when you have multiple numbers in each $\vec{x}$ each of the dimensions can impinge on each other for example in the case of a rotation—in physics it doesn't matter which orthonormal coördinate system you choose, so we want to "quotient away" that invariant our physical theories.