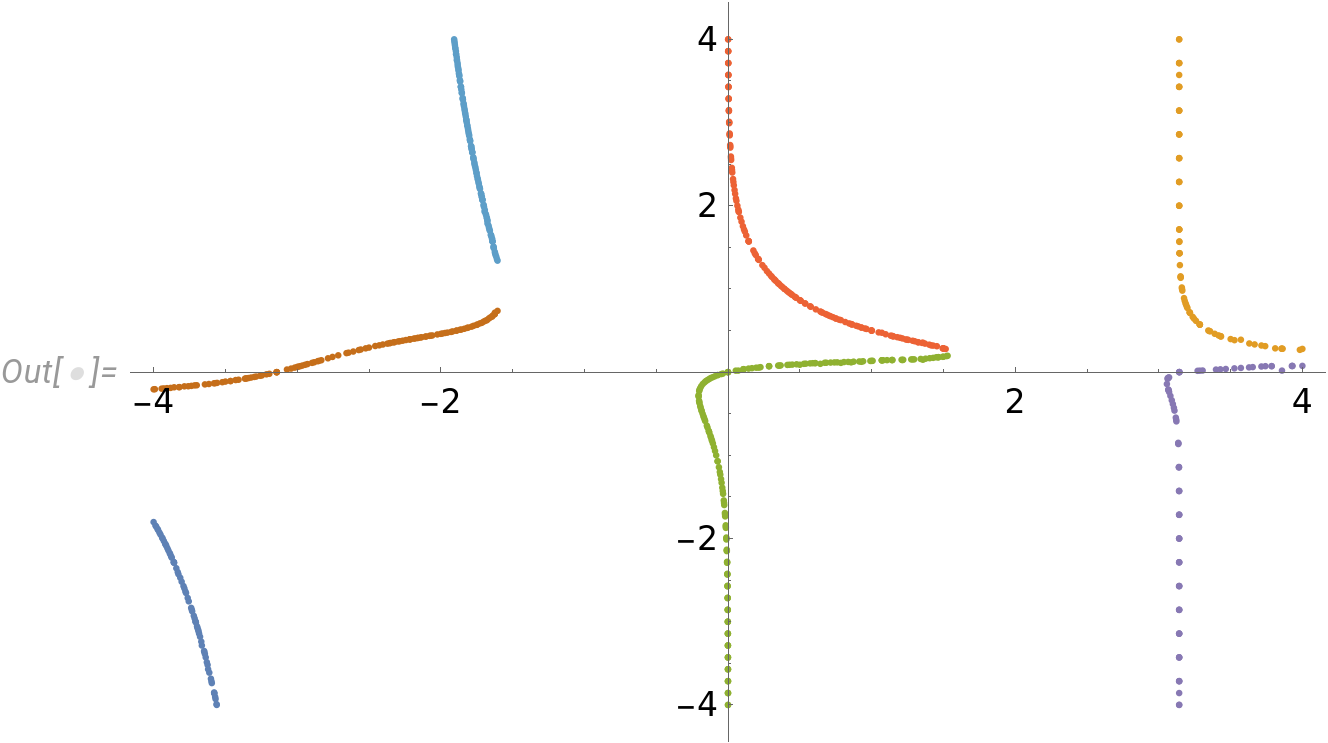0
$\begingroup$

I have an equation

$$ c \tan \left(\theta_{\mathrm{OPT}}\right)+\frac{a b A \exp \left(-b\left[\theta_{\mathrm{OPT}}-a\right]\right)}{\left[a \exp \left(-b\left[\theta_{\mathrm{OPT}}-a\right]\right)+1\right]^2}=0 $$

where a,b,c and A are constants. How can I solve this equation for $\theta_{OPT}$. Also is there any possibility to solve this equation in matlab/mathematica. I have tried taking natural log on both sides but it does not works.

I have tried the solve function in mathematica solve(((a b A exp(-b (x - a)))/(a exp(-b (x - a)) + 1)^2 = -c tan(x)),x)

Improve this question
$\endgroup$
10
  • 1
    $\begingroup$ A numerical solution for given parameters isn't sufficient? $\endgroup$ Commented Dec 13, 2022 at 12:02
  • $\begingroup$ Welcome to the Mathematica Stack Exchange. Please share copy-paste-able Mathematica code for what you have tried so far. What are the constraints on the various constants? $\endgroup$ Commented Dec 13, 2022 at 12:18
  • $\begingroup$ Thanks, I have added mathematica pastable format above $\endgroup$ Commented Dec 13, 2022 at 12:45
  • $\begingroup$ Maybe that is matlab syntax. You used solve instead of Solve and exp(-b (x - a)) instead of Exp[-b (x - a)]. Consider copy pasting the code from your Mathematica notebook. $\endgroup$ Commented Dec 13, 2022 at 15:13
  • $\begingroup$ It does not seem like Mathematica can solve that equation symbolically. Consider seperately the case c=0 and then divide by c and change A to w*c for example to absorb the c. That way you have one less parameter to consider when numerically solving the problem. That said you might want to revert to the previous coordinates after. For a graphical method of finding roots consider : mathematica.stackexchange.com/a/272002/86543. $\endgroup$ Commented Dec 13, 2022 at 15:47

1 Answer 1

Reset to default
1
$\begingroup$ 
expression = (a b A Exp[-b (x - a)])/(a Exp[-b (x - a)] + 1)^2 + c Tan[x]

$$ \frac{a A b e^{-b (x-a)}}{\left(a e^{-b (x-a)}+1\right)^2}+c \tan (x) $$

Outline :

  • 1) Removing c from the parameters

  • 2) Finding some analytical solutions using FindInstance

  • 3) Using Manipulate and ContourPlot to find roots in an equation with many parameters

  • 4) Extracting the points from a given contour plot

  • 5) Polishing results with better accuracy

1) Removing c from the parameters

For non zero c, we can absorb the dependence on c by dividing by c and using A->c*w :

expression2 = expression/c /. A -> w*c // Simplify

$$\frac{a b w e^{b (x-a)}}{\left(e^{b (x-a)}+a\right)^2}+\tan (x)$$

That way there is one less parameter to consider but do not forget to check separately the case c=0. In the following I will focus on c non zero.

2) Finding some analytical solutions using FindInstance

For generic parameters Mathematica can not find a root for expression above. However, it can find instances of roots using FindInstance. For example, if we consider a to be positive then :

FindInstance[{expression2 == 0, a > 0}, {x, a, b, w}]

{{x->9392403/3312026,a->26566113/18118801,b->30971405/14149612,w->-((256374004055212 (26566113/18118801+E^(2545583876943569930325/849117367154967579512))^2 Tan[9392403/3312026])/(822789844998765 E^(2545583876943569930325/849117367154967579512)))}}

If you want a symbolic solution regardless of whether the solution is in terms of the variable x or one of the parameters, consider Solve or Reduce.

3) Using Manipulate and ContourPlot to find roots in an equation with many parameters

We can visualize dependence on parameters using (recall that c=0 should be considered separately):

Note: I chose the ranges of parameters in an arbitrary manner

 With[{expression2 = expression2}, Manipulate[ ContourPlot[expression2 == 0, {x, -4, 4}, {b, -4, 4}], {a, -4, 4}, {w, -4, 4}]]

enter image description here

4) Extracting the points from a given contour plot

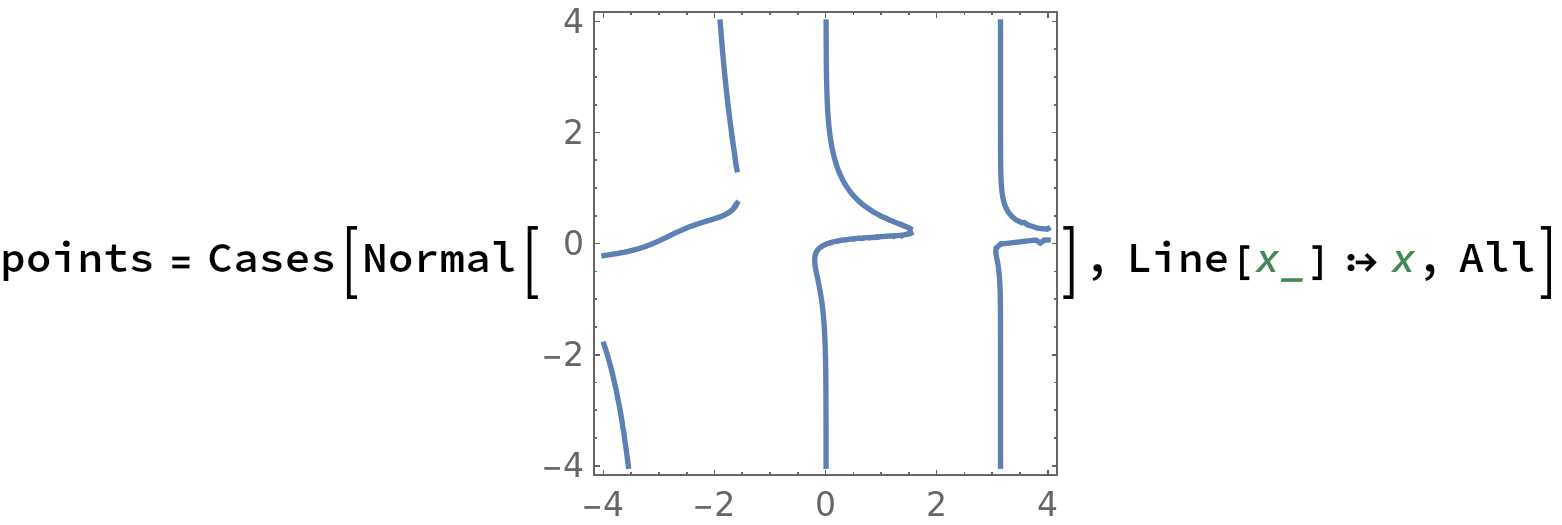
If you want to extract the lines from a given value of a and w you can right click the plot and copy it and then paste into a new cell and use :

template of code below : points = Cases[Normal[... plot here ...], Line[x_] :> x, All]

enter image description here

The points:

points // ListPlot

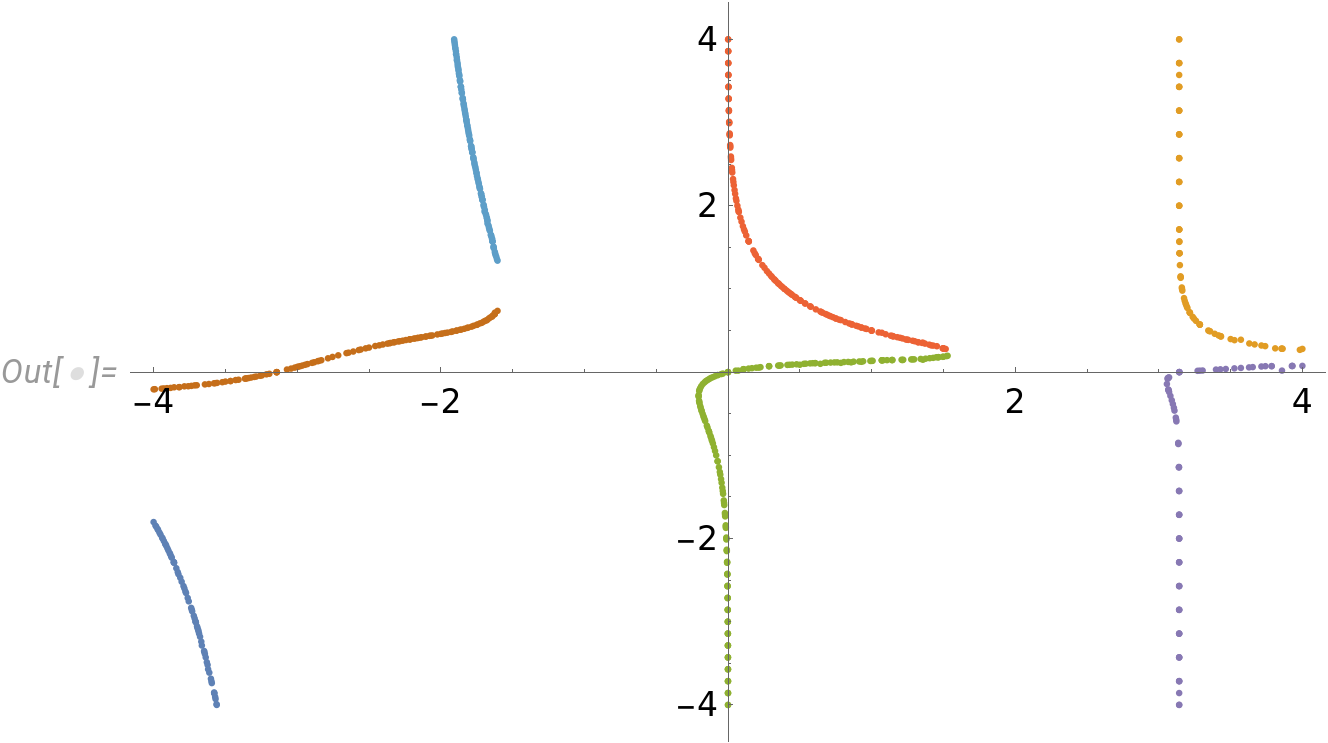
enter image description here

5) Polishing results with better accuracy

The points above might not be very accurate. In that case consider the numerical methods here: How to find seed values for solving nonlinear equations?

Improve this answer
$\endgroup$

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.